机器学习 | 朴素贝叶斯

机器学习 | 朴素贝叶斯

更多内容，关注wx公众号：数据分析这件小事儿

贝叶斯派与频率派
在参数估计上，有两个方法，MLE（最大似然估计） 和MAP（最大后验估计），分别代表了频率派和贝叶斯派。

频率派关心的是似然函数，认为用样本去计算出的概率就是真实的，而贝叶斯派关心的是后验分布，他们认为样本只是用来修正经验观点。

贝叶斯学派的思想可以概括为先验概率+数据=后验概率，即实际问题中需要得到的后验概率，可以通过先验概率和数据一起综合得到。

先验概率：指根据以往经验和分析，在实验或采样前就可以得到的概率。

后验概率：指某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。

先验概率就是事先可估计的概率分布，而后验概率类“由果溯因”的思想。由于先验概率常常难以量化，所以这一点常常被频率派攻击，他们认为贝叶斯派假设的先验分布模型，比如正态分布，beta分布等，没有特定的依据。

贝叶斯公式
假设将训练数据分为k类，如果知道条件概率，则最优预测应最大化此条件概率，也称后验概率：

上式表明，对于y的预测，应使后验概率最大化，这种决策方法称为贝叶斯最优决策，由此得到的决策边界叫做贝叶斯决策边界。使用贝叶斯最优决策，达到的错误率，叫做贝叶斯错误率或贝叶斯风险。

贝叶斯公式可表示为：

P(yi=k)为看到x=xi之前的先验概率，P(x=xi|yi=k)为给定类别yi=k的条件概率密度。但事实上条件概率很难估计，由于特征向量xi可以是连续、离散和混合型随机向量，故有时无法假设xi服从多维正态分布，并且维度也可能很高。例如在用词频判断是否是垃圾邮件的时候，由于关键词成千上万，得到的数据一般为高维的稀疏矩阵，故不易估计其协方差矩阵，这也是维度灾难的一种表现形式。

我们把贝叶斯公式中的x理解为“具有某特征”，把y理解成“类别标签”，那么贝叶斯公式就可以表示为：

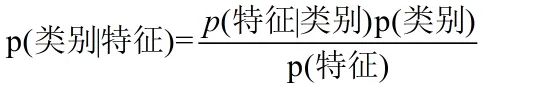
从上式看出，贝叶斯法就是把计算“具有某特征条件下属于某类（就是分类）”的概率转化为需要计算“属于某类条件下具有某特征（分别训练模型）”的概率。
朴素贝叶斯与决策边界
为简化计算，朴素贝叶斯分类器对高维的条件概率做了各特征之间相互独立的假定，这就是“朴素”的含义，这就相当于将高维数据，转化成了一维数据，此时条件概率可表示为连乘的形式：

给定x=xi，为比较第k类与第l类的后验概率，将二者相除，可得后验几率，也称为“似然比”：

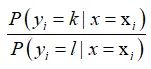
若上式>1，则可预测属于第k类，若上式=1，则为决策边界。

简单地讲，朴素贝叶斯是基于贝叶斯定理和特征条件独立假设的分类方法，首先学习输入/输出的联合概率分布，然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y，属于生成模型。
拉普拉斯修正
零概率事件指的是在计算事件的概率时，如果某个事件在训练集中没有出现过，会导致该事件的概率结果是0。这是不合理的，不能因为一个事件没有观察到，就被认为该事件一定不可能发生（即该事件的概率为0）。

法国数学家 拉普拉斯 最早提出用“加1”的方法，估计没有出现过的现象的概率，假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。

具体的应用案例：

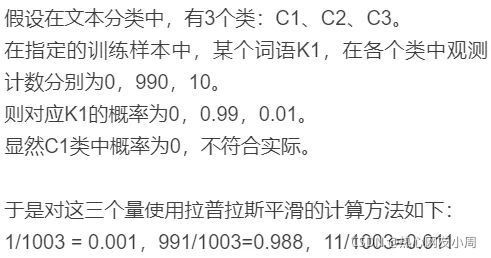
因此，为了避免其他属性携带的信息被训练集中未出现的属性值"抹去’，在估计概率值时通常需要进行"平滑" ，"拉普拉斯修正"就为最常用的方法。

拉普拉斯修正实质上假设了属性值与类别均匀分布，拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题，并且在训练集变大时，修正过程所引入的先验的影响也会逐渐变得可忽略，使得估值渐趋向于实际概率值。
朴素贝叶斯算法过程
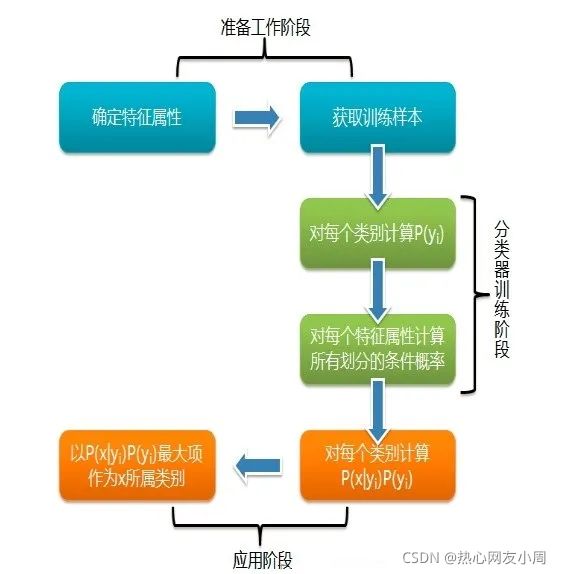
第一阶段：准备阶段

确定特征属性，同时明确预测值是什么，并对每个特征属性进行适当划分，然后由人工对一部分数据进行分类，形成训练样本，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段：训练阶段

生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率，此阶段输入的是特征属性和训练样本，输出是分类器。

第三阶段：应用阶段

这个阶段是使用分类器对新数据进行分类，输入是分类器和新数据，输出是新数据的分类结果。

参考资料：

1.陈强 《机器学习及Python应用》高等教育出版社

2.李航 《统计学习方法(第二版)》清华大学出版社

3.周志华 《机器学习》清华大学出版社

4.https://github.com/wangyuGithub01/Machine_Learning_Resources

5.https://www.cnblogs.com/pinard/p/6069267.html

6.https://blog.csdn.net/qiu_zhi_liao/article/details/90671932

7.https://blog.csdn.net/qq_25073545/article/details/78621019

8.https://blog.csdn.net/weixin_43593330/article/details/105797717