卡尔曼滤波——多目标追踪代码实现详解
import numpy as np
import scipy.linalg
"""
Table for the 0.95 quantile of the chi-square distribution with N degrees of
freedom (contains values for N=1, ..., 9). Taken from MATLAB/Octave's chi2inv
function and used as Mahalanobis gating threshold.
"""
chi2inv95 = {
1: 3.8415,
2: 5.9915,
3: 7.8147,
4: 9.4877,
5: 11.070,
6: 12.592,
7: 14.067,
8: 15.507,
9: 16.919}
class KalmanFilter(object):
"""
A simple Kalman filter for tracking bounding boxes in image space.
The 8-dimensional state space
x, y, a, h, vx, vy, va, vh
contains the bounding box center position (x, y), aspect ratio a, height h,
and their respective velocities.
bounding box的中心点的位置,长宽比啊,高度h以及他们各自的速度。
Object motion follows a constant velocity model. The bounding box location
(x, y, a, h) is taken as direct observation of the state space (linear
observation model).
"""
def __init__(self):
ndim, dt = 4, 1.
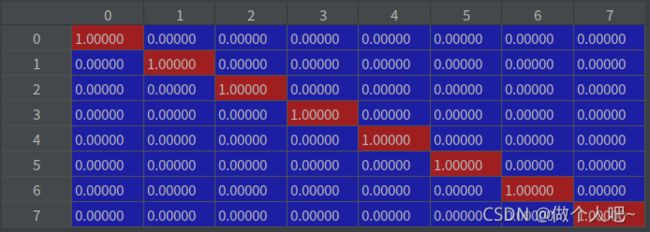
#创建卡尔曼滤波器模型矩阵。 Fk控制矩阵
# Create Kalman filter model matrices.
self._motion_mat = np.eye(2 * ndim, 2 * ndim)
np.eye(2 * ndim, 2 * ndim)
for i in range(ndim):
self._motion_mat[i, ndim + i] = dt
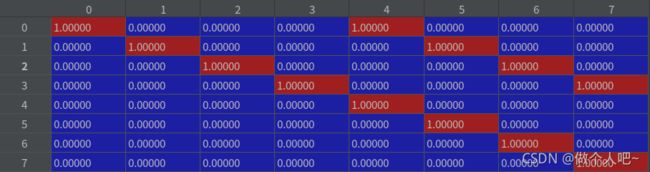
self._update_mat = np.eye(ndim, 2 * ndim)
# Motion and observation uncertainty are chosen relative to the current
# state estimate. These weights control the amount of uncertainty in
# the model. This is a bit hacky.
#相对于当前状态估计,选择运动和观测不确定性。这些权重控制模型中的不确定性量。这有点老套。
self._std_weight_position = 1. / 20
self._std_weight_velocity = 1. / 160
def initiate(self, measurement):
"""Create track from unassociated measurement.
Parameters
----------
measurement : ndarray
Bounding box coordinates (x, y, a, h) with center position (x, y),
aspect ratio a, and height h.
Returns
-------
(ndarray, ndarray)
Returns the mean vector (8 dimensional) and covariance matrix (8x8
dimensional) of the new track. Unobserved velocities are initialized
to 0 mean.
"""
mean_pos = measurement
mean_vel = np.zeros_like(mean_pos)
mean = np.r_[mean_pos, mean_vel]
std = [
2 * self._std_weight_position * measurement[3],
2 * self._std_weight_position * measurement[3],
1e-2,
2 * self._std_weight_position * measurement[3],
10 * self._std_weight_velocity * measurement[3],
10 * self._std_weight_velocity * measurement[3],
1e-5,
10 * self._std_weight_velocity * measurement[3]]
covariance = np.diag(np.square(std))
return mean, covariance
def predict(self, mean, covariance):
"""Run Kalman filter prediction step.
Parameters
----------
mean : ndarray
The 8 dimensional mean vector of the object state at the previous
time step.
covariance : ndarray
The 8x8 dimensional covariance matrix of the object state at the
previous time step.
Returns
-------
(ndarray, ndarray)
Returns the mean vector and covariance matrix of the predicted
state. Unobserved velocities are initialized to 0 mean.
"""
std_pos = [
self._std_weight_position * mean[3],
self._std_weight_position * mean[3],
1e-2,
self._std_weight_position * mean[3]]
std_vel = [
self._std_weight_velocity * mean[3],
self._std_weight_velocity * mean[3],
1e-5,
self._std_weight_velocity * mean[3]]
motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))
#mean = np.dot(self._motion_mat, mean)
mean = np.dot(mean, self._motion_mat.T)
covariance = np.linalg.multi_dot((
self._motion_mat, covariance, self._motion_mat.T)) + motion_cov
return mean, covariance
def project(self, mean, covariance):
"""Project state distribution to measurement space.
Parameters
----------
mean : ndarray
The state's mean vector (8 dimensional array).
covariance : ndarray
The state's covariance matrix (8x8 dimensional).
Returns
-------
(ndarray, ndarray)
Returns the projected mean and covariance matrix of the given state
estimate.
"""
std = [
self._std_weight_position * mean[3],
self._std_weight_position * mean[3],
1e-1,
self._std_weight_position * mean[3]]
innovation_cov = np.diag(np.square(std))
mean = np.dot(self._update_mat, mean)
covariance = np.linalg.multi_dot((
self._update_mat, covariance, self._update_mat.T))
return mean, covariance + innovation_cov
def multi_predict(self, mean, covariance):
"""Run Kalman filter prediction step (Vectorized version).
Parameters
----------
mean : ndarray
The Nx8 dimensional mean matrix of the object states at the previous
time step.
covariance : ndarray
The Nx8x8 dimensional covariance matrics of the object states at the
previous time step.
Returns
-------
(ndarray, ndarray)
Returns the mean vector and covariance matrix of the predicted
state. Unobserved velocities are initialized to 0 mean.
"""
std_pos = [
self._std_weight_position * mean[:, 3],
self._std_weight_position * mean[:, 3],
1e-2 * np.ones_like(mean[:, 3]),
self._std_weight_position * mean[:, 3]]
std_vel = [
self._std_weight_velocity * mean[:, 3],
self._std_weight_velocity * mean[:, 3],
1e-5 * np.ones_like(mean[:, 3]),
self._std_weight_velocity * mean[:, 3]]
sqr = np.square(np.r_[std_pos, std_vel]).T
motion_cov = []
for i in range(len(mean)):
motion_cov.append(np.diag(sqr[i]))
motion_cov = np.asarray(motion_cov)
mean = np.dot(mean, self._motion_mat.T)
left = np.dot(self._motion_mat, covariance).transpose((1, 0, 2))
covariance = np.dot(left, self._motion_mat.T) + motion_cov
return mean, covariance
def update(self, mean, covariance, measurement):
"""Run Kalman filter correction step.
Parameters
----------
mean : ndarray
The predicted state's mean vector (8 dimensional).
covariance : ndarray
The state's covariance matrix (8x8 dimensional).
measurement : ndarray
The 4 dimensional measurement vector (x, y, a, h), where (x, y)
is the center position, a the aspect ratio, and h the height of the
bounding box.
Returns
-------
(ndarray, ndarray)
Returns the measurement-corrected state distribution.
"""
projected_mean, projected_cov = self.project(mean, covariance)
chol_factor, lower = scipy.linalg.cho_factor(
projected_cov, lower=True, check_finite=False)
kalman_gain = scipy.linalg.cho_solve(
(chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
check_finite=False).T
innovation = measurement - projected_mean
new_mean = mean + np.dot(innovation, kalman_gain.T)
new_covariance = covariance - np.linalg.multi_dot((
kalman_gain, projected_cov, kalman_gain.T))
return new_mean, new_covariance
def gating_distance(self, mean, covariance, measurements,
only_position=False, metric='maha'):
"""Compute gating distance between state distribution and measurements.
A suitable distance threshold can be obtained from `chi2inv95`. If
`only_position` is False, the chi-square distribution has 4 degrees of
freedom, otherwise 2.
Parameters
----------
mean : ndarray
Mean vector over the state distribution (8 dimensional).
covariance : ndarray
Covariance of the state distribution (8x8 dimensional).
measurements : ndarray
An Nx4 dimensional matrix of N measurements, each in
format (x, y, a, h) where (x, y) is the bounding box center
position, a the aspect ratio, and h the height.
only_position : Optional[bool]
If True, distance computation is done with respect to the bounding
box center position only.
Returns
-------
ndarray
Returns an array of length N, where the i-th element contains the
squared Mahalanobis distance between (mean, covariance) and
`measurements[i]`.
"""
mean, covariance = self.project(mean, covariance)
if only_position:
mean, covariance = mean[:2], covariance[:2, :2]
measurements = measurements[:, :2]
d = measurements - mean
if metric == 'gaussian':
return np.sum(d * d, axis=1)
elif metric == 'maha':
cholesky_factor = np.linalg.cholesky(covariance)
z = scipy.linalg.solve_triangular(
cholesky_factor, d.T, lower=True, check_finite=False,
overwrite_b=True)
squared_maha = np.sum(z * z, axis=0)
return squared_maha
else:
raise ValueError('invalid distance metric')
对于算法输入为均值和方差矩阵
multi_mean, multi_covariance = STrack.shared_kalman.multi_predict(multi_mean, multi_covariance)
multi_mean
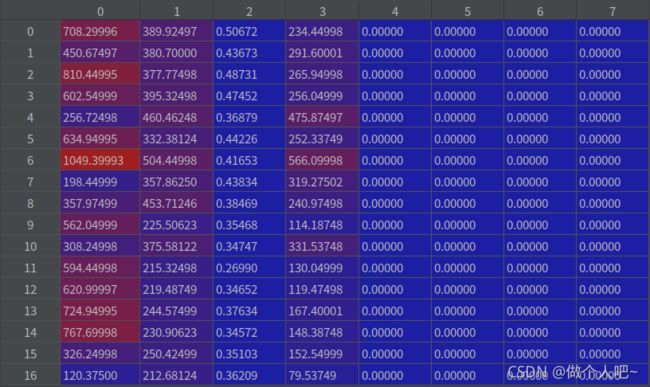
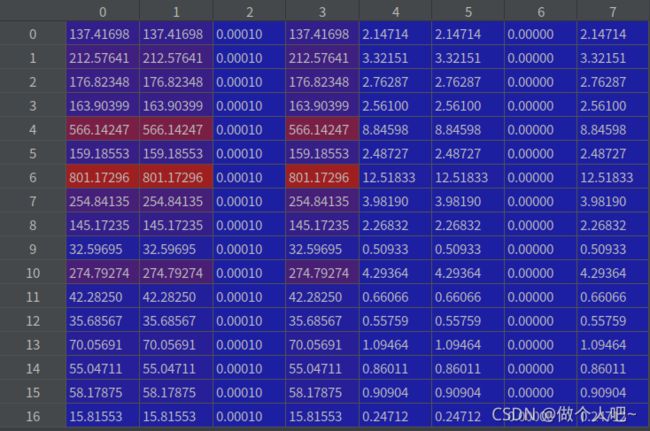
multi_covariance
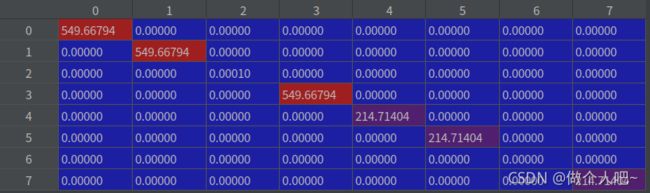
在multi_predict函数中进行更新(预测)
假设为不受外力干扰的运动
mean = np.dot(mean, self._motion_mat.T)
其中motion_cov为预测方差,其产生方法为
std_pos = [
self._std_weight_position * mean[:, 3],
self._std_weight_position * mean[:, 3],
1e-2 * np.ones_like(mean[:, 3]),
self._std_weight_position * mean[:, 3]]
std_vel = [
self._std_weight_velocity * mean[:, 3],
self._std_weight_velocity * mean[:, 3],
1e-5 * np.ones_like(mean[:, 3]),
self._std_weight_velocity * mean[:, 3]]
sqr = np.square(np.r_[std_pos, std_vel]).T
motion_cov = []
for i in range(len(mean)):
motion_cov.append(np.diag(sqr[i]))
motion_cov = np.asarray(motion_cov)
left = np.dot(self._motion_mat, covariance).transpose((1, 0, 2))
covariance = np.dot(left, self._motion_mat.T) + motion_cov