几何算法——6.曲线曲面求交的方法总结（国内外文献调研、思考和总结）

1 曲线曲线

1.1 直线/二次曲线

直接解析法计算交点。

1.2 二次曲线/二次曲线

// Todo

1.3 其他类型

（1992年11月）NURBS求交算法一一曲线部分（姜寿山 刘雄伟/西安工业学院 西北工业大学）

摘要 NURBS曲线的R-Rect求交方法通过改变曲线凸包的形状而使得凸包与曲线 贴得更近，减少曲线的细分次数，从而提高了计算速度 文中给出具体的实现过 程、流程图和实例 经过实用系统的验证，这种未交算法具有稳定、可靠和速度快 的特点。这种方法还可以非常方便地推广到曲面求交中去。
关键饲 B一样条 凸包求交 NURBS曲线

常用以下三种凸包，即自然凸包、矩形凸包和斜矩形凸包，分别记为Box方法、Rect方法和R-Rect方法.
斜矩阵凸包方法如下:首先构造局部坐标系，P0为局部坐标系的原点，P0P3为局部坐标系的x方向，相应地可以得出它的Y方向。然后此坐标系下的斜矩形包围盒。//主要是应用于nurbs的控制顶点凸包计算。

评论：对于nurbs求交，使用斜包围盒的计算有一定的参考意义。但是本文计算方法的精度不够，还是得迭代求交比较好。

（2003年）二次曲线求交的交叉迭代法研究（李平 王琨琦/西安工业学院）

摘要 针对机械制造中的二次曲面或二次曲线的求交问题，本文提出了交叉迭代法，并从理论上详细分析了交叉迭代法，证明了交叉迭代法的收敛性该方法解决了我国机械制造中数控自动编程的一个基本问题。
关键词:二次曲线;交叉迭代法;数字控制;自动编程
评论：文中用的迭代求交的方法，初值的计算方法没有什么巧妙之处，然后从初值开始迭代。文中说证明了收敛，但是我表示怀疑，迭代收不收敛与初值有很大关系，但文中的计算初值方法并没有特殊处理方法。感觉实际价值不会太大。

（2004年10月）一种快速求取空间任意两条曲线交点的算法（董明晓 郑康平/山东建筑工程学院 西安交通大学）

摘要 求空间两条曲线的交点是CAD/CAE重要内容之一，它的准确性与效率直接影响系统的可 靠性与实用性。通常是将两条曲线的方程联立求解，或者是对曲线建立包围盒。但上述两种方法计算量 较大，甚至求解困难。这里提出一种快速实用的曲线求交算法，具有较高的稳定性和可靠性。该算法分两 步进行，首先根据P样条曲线的控制多边形判断两条曲线是否相交，并求出两条曲线存在交点的可能参 数区间，然后在此区间内，利用控制顶点算出所对应的曲线段，进行精确求交计算。与常用的包围盒方法 相比，该算法效率高、精度易于控制，并通过实例验证算法的有效性。
关键词：曲线求交；算法；P样条曲线；自由曲线

判断两条曲线是否有可能相交，可利用控制多边形进行判 断，如果两条曲线的控制多边形存在相交的可能，则两条曲线 也同样存在相交的可能。判断方法如下：首先取两条曲线控制 多边形的第i边和第j边，两个边 的相对位置有四种情况，逐一分析处理。控制多边形所有边两两判断，可判断空间两条曲线是否可能相交， 以及交点所位于的曲线段。对于可能相交的段，精确求交。

评论：感觉方法效率应该不会太高，精度可能也一般。实际价值不大。

（2005年11月）平面椭圆与二次曲线间位置关系的判别式（陈小雕 雍俊海 郑国勤 孙家广/清华大学）

摘要 平面实体间的碰撞检测中，经常需要讨论二次曲线间的位置关系∙根据切点既是交点，又是最近/最远距离 点的性质，结合结式理论推导出若干代数多项式，并用来判定平面椭圆与二次曲线间的位置关系∙该方法直观简单， 仅需要简单四则运算，可以直接应用于判别运动曲线间的位置关系∙最后的实例及其比较表明，该方法应用范围广，结果也稳定∙
关键词　碰撞检测；平面椭圆/二次曲线的位置关系；判别式；最近/最远距离
$$\begin{gathered} S_1(x,y）＝a_1{x}^2＋2b_{1}xy＋c_1{y}^2＋2d_{1}x＋2e_{1}y＋f_1 \\ {S}_2(x,y）＝a_2{x}^2＋2b_{2}xy＋c_2{y}^2＋2d_{2}x＋2e_{2}y＋f_2 \end{gathered}$$
椭圆$S_R$与二次曲线C相切，切点(x,y)既是交点，同时又满足2条曲线在切点处相切，则有
// 注：利用相切条件，即切向（偏微分方向相同，但是长度大小可能不同），对上式进行微分可得到下面方程组中的第3、4方程。
$$\begin{gathered} a1x2＋2b1xy＋c1y2＋2d1x＋2e1y＋R＝0 \\ a2x2＋2b2xy＋c2y2＋2d2x＋2e2y＋f2＝0 \\ （a1x＋b1y＋d1）＋k（a2x＋b2y＋d2）＝0 \\ （b1x＋c1y＋e1）＋k（b2x＋c2y＋e2）＝0\text{\hspace{1em}(1)} \end{gathered}$$

其中k为新引入的变量.从式(1)中可以解出：
$$\begin{gathered} x＝\frac{（e1＋e2k）（b1＋b2k）－（c1＋c2k）（d1＋d2k）}{（a1＋a2k）（c1＋c2k）－（b1＋b2k）2} \\ y＝\frac{（d1＋d2k）（b1＋b2k）－（a1＋a2k）（e1＋e2k）}{（a1＋a2k）（c1＋c2k）－（b1＋b2k）2}\text{\hspace{1em}(2)} \end{gathered}$$
将式（2）重新代入式（1 ）中的前2个子方程，得到两 个关于变量k的4次有理多项式，分别记为g（k）和h（k），其中g（k）是关于变量R的一次多项式， h（k）与R无关。结合结式理论从式g（k），h（k）中消去k，得到关于变量R的一元4次多项式f（R），即有
$$f(R）＝l_0＋l_{1}R＋l_2{R}^2＋l_3{R}^3＋l_4{R}^4（3）$$
若f（R）不退化,约定$l_4＞0$,并称该多项式f（R）为 位置关系的判别多项式∙由于最小临界值R1始终 存在，则4次多项式f（R）或者有2个实根，或者有个实根。如图1所示。

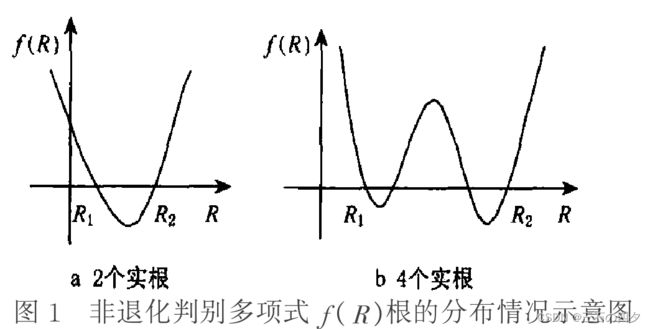
在通过分析这个多项式f（R）来判定椭圆与二次曲线的位置关系。文中分别分析了椭圆与椭圆、椭圆与抛物线、椭圆与双曲线的各种情形的分析，得出位置关系的判定方法。
与直接粗暴求解的一元四次方程的解优点在于：求根由于涉及到复杂的开方运算，计算量大，并且求根结果对于系数非常敏感，常常由于有限精度的影响而变得不稳定，特别是临界情况会发生误判。本文方法不需要具体求根，计算简单，结果也更加稳定、合理.

（2007年9月）基于曲率圆的平面参数曲线求交算法（张松海 黄智勇/清华大学）

摘　要　主要讨论了平面参数曲线求交的迭代算法，提出了迭代过程中迭代可信度的概念，并给出了计算方法．在 此基础上，改进了MAF求交算法，给出了曲率圆迭代算法，即使用二次曲线对参数曲线的局部形状进行近似，进行迭代交点和迭代步长的计算。
关键词　迭代可信度；MAF求交；曲率圆

求交算法主要分为:代数方法、细分方法和迭代方法或几种方法的综合代数方法[1-2]主要基于消去理论和root finding，它在处理5次以下的曲线时是速度最快的。细分方法[3-4]是一种鲁棒的方法，它可以找到所有的交点，但是收敛速度很低，并且会消耗大量的内存迭代方法，例如牛顿法[5]和求交算法MAF(Moving Affine Frame)[6-7]，在一般情况下，速度是最快的，但是它们是初值敏感的。

二阶估计比一阶估计(直线)更贴近原来的曲线，所以它在该点处保留了原曲线更多的局部特征同时，将迭代步长值限制在某个最大值之内，使得每次迭代的步长值都是可靠的这个最大值是通过近似的误差计算出来的，称为迭代可信度。

传统MAF算法使用直线来近似曲线一点处的局部特征。并使用两条直线的最短距 离点来计算迭代步长值．曲线的二次估计更加逼近 曲线，保留了更多局部特征，使用曲线的二次近似计 算迭代步长值，可以使步长的计算更加准确，特别是 提高了步长的方向的准确性，从而加快收敛速度．

// 思考：在一维方程求解，有牛顿迭代法；当牛顿迭代在二重根和多重根的时候迭代效率很慢；但是还有二次插值法，迭代效率会比较高一些。二次插值之所以能用，是因为二次方程能直接求根。这个地方，对于二元非线性方程组，如果也想用二次插值法，都用二次插值逼近，得到的是二元二次方程组，但是二元二次方程组，没办法直接求根（交点）。但是可以利用圆的特殊性，两个圆是可以直接计算最近点或交点的，也就是本文的办法，用两个圆来逼近曲线。//注，用二次插值有两种好处，一个是本身迭代效率高，一个是对于相切（二重根）收敛也快（普通牛顿迭代，遇上二重根的情况，收敛速度就会变成线性的）。
//文中结尾提到，对于三维空间的曲率圆计算最近距离会变得相对比较复杂，目前主要用于二维平面曲线的求交。

评论：虽然说没有实现过，但是感觉这种方法很有用（甚至可能对于相切（二重根）的情况收敛速度应该也不错，文中没有提到，需要自己实际测试一下），可用于实际中。
但是，文末提到的，“本文提出的算法相对传统MAF算法，增加了二阶导数、三 阶导数的计算量，由于只用来估计迭代可信度，可以 不用计算二阶、三阶导数，而使用以前迭代步中计算过的在迭代点附近的曲线点的位置和一阶导数来近似．这样可以进一步提高算法的效率。”最后一句很关键，但是不是很理解，怎么近似的。

（2005年6月）吴消元法的初等代数形式（刘洪林 刘洪元/沈阳农业大学）

摘要：通过对吴文俊先生“解方程器或SOLVER软件系统”的研究，发现吴消元法的理论根据是里特－吴整序原理，吴消元法的运算过程主要是对多项式约化求余式，这些都可以在初等数学中找到相应的解释．研究里特－吴整序原理与同解方程组之间的关系，写出吴消元法的初等代数形式，从而找到学习推广吴消元法的一般途径．
关　键　词：吴消元法; 多项式方程组; 里特一吴整序原理; 伪除法

评论：吴消元法对于解多项式方程组是一个不错的方法思路。

（2014年5月）实系数二元二次方程组实根分类求解方法（万瑞杰 雍俊海 施侃乐/清华大学）

摘 要：为了提高平面二次曲线求交结果的精度和拓扑稳定性，提出一种基于二次曲线分类的二元二次方程组实根求解方法 ． 首先将二元二次方程组的 ２ 个方程依照系数判断出其在$ｘ-ｙ$平面上的曲线类型，并根据不同的曲线类型分类情况，应用曲线的参数方程将原方程组转化为一元四次方程；然后求解出一元四次方程的解，并依此求出原二元二次方程组的解 ． 实验结果表明，与吴消元法相比，该方法有效地提高了二元二次方程组求解的精度 ．
关键词：二元二次方程组；实根求解；几何分类；参数方程；二次曲线

代数方程求解从数学上可以分为数值求解和根式求解方法２类．数值求解方法适用于所有方程求解问题，通过选择合适的初始数值进行迭代，从而得到方程的解；但是这种直接在原方程组上进行迭代求解方法目前在初始值的确定以及解的完备性等方面仍然存在一定的问题．要使用根式求解方法，则需要将原来的方程组转换成一元方程，同时一元方程要在四次以下，再进行求解．
（然而在计算机领域中，由于浮点数计算存在截断误差，使得在计算方程解的过程中会产生误差，甚至还会使求得的方程解的个数和实际方程解的个数不同．二元二次方程实根求解计算中的误差来自于２部分，即一元方程的求解和二元二次方程组向一元方程转换的过程．）

如果曲线是一次型，直接带入解一元二次方程。
如果曲线类型属于二次型，首先将其转化为对应的参数方程形式，然后将其代入到另一个方程形成一元四次方程，通过求解该一元四次方程最终确定原方程组的解．

测试案例分为３类：４个不相同的实根、２个不相同的实根和一组共轭虚根、２组共轭虚根．

当２个方程都是二次型时，会面临选择将哪一个方程转换成参数方程的问题．类似地，在实际应用吴方法求解时，也会面临选择消去 ｘ 和 ｙ 哪一个形成一元方程的问题．本文采取的方法是将２种选择都进行一遍，形成２个一元四次方程后，比较２个一元四次方程的系数，选择参数较小的方案进行求解．

总结：在精度方面，基于分类的方法要优于吴方法，误差要更低一些；在效率方面，基于分类的方法要比吴方法运行时间要略长一些（其实相差也不多）．//可以用来在实际应用中实现。

（2013年5月）三次Ｂ样条曲线的重合判断算法（王文珂 李思昆/国防科学技术大学）

摘要：曲线和曲线求交计算是ＣＡＧＤ领域的一个基本问题，但现有的求交算法都无法处理曲线重合的情况．在２ 条三次Ｂéｚｉｅｒ曲线重合判断条件的基础上，提出一种判断２条三次Ｂ样条曲线是否重合的算法．对于每条Ｂ样条曲 线，首先将其分割成若干Ｂéｚｉｅｒ曲线段，然后判断２条Ｂéｚｉｅｒ曲线段是否可以合并为一段；通过合并Ｂéｚｉｅｒ曲线段， 将２条三次Ｂ样条曲线的重合判断问题转化为２组三次Ｂéｚｉｅｒ曲线段的重合判断问题．文中在理论上证明了该算法 的正确性，并通过若干实例验证了其有效性． 关键词：三次Ｂ样条曲线；重合判断；Ｂézier曲线合并；曲线求交

曲线重合是不可避免的．为了增强系统的鲁 棒性，在进行曲线求交之前，必须先对曲线重合的情 况进行判断和处理．

两条三次Bezier曲线重合的方法是不难的，文献［６］给 出了一个简洁的结论：２条三次Ｂéｚｉｅｒ曲线重合，当 且仅当它们对应的控制点相同，或者一条曲线是另 一条曲线的反转曲线．

对于样条曲线的重合判断，先分割成Ｂéｚｉｅｒ曲线段，并合并可以合并 的Ｂéｚｉｅｒ曲线段，２条三次Ｂ样条曲线的重合判断 可以转化为２组三次Ｂéｚｉｅｒ曲线段的重合判断．

//评论：这种判断重合的方法感觉还不错，但是不知道效率如何（感觉效率可能一般？），还需在实践中测试一下。

2 曲线曲面

2.1 直线/二次曲面，二次曲线/平面

直接解析法计算交点。

2.2 二次曲线/二次曲面

// Todo

2.3 其他类型

（1996年8月）曲线曲面的若干几何处理基础算法研究（冉瑞江 王亚平 马德昌 唐荣锡/北航飞行器制造工程系）

注：这篇文章主要讲一些曲线曲面离散、点线面投影的算法，在文末才简单介绍了直线和圆环面的求交方法。

直线-圆环的求交算法十分简明．如图6所示，圆环中心为 C，A 为中心轴，R 和 r 意义如图所示．空间一点 P，容易求得它离圆环平面（ 过C 点以 A 为法矢的平面） 高度为 h，离中心轴 A 距离为 d，则 P 点在圆环上的充要条件为$(d－R{)}^2＋h^2＝r^2$ ,P 点在直线上：
$$\begin{gathered} P＝P（t）＝P_0＋t\ast V（12） \\ h＝［A］\ast ［P（t）－C］（13） \\ {d}^2＝(|P(t）-C{|}^2－h^2)（14） \end{gathered}$$
把（ 13） 、（ 14） 式代入（ 12） 式，得到关于 t 的4次方程，解此方程即得到直线-圆环的全部交点．

（2005年9月）基于坐标变换的曲线曲面求交算法（陈晓霞 雍俊海 陈玉健 刘辉/兰州理工大学 清华大学）

摘要 利用坐标变换的方法,给出了二次曲线和二次曲面求交的解析算法。利用拉格朗日乘子法求解二次 曲线和二次曲面之间的最小距离,给出了曲线与曲面相切的条件。算法表明,坐标变换可以简化求交运算表达式, 使求交算法易于实现。根据得出的相切条件,可以有效地判断曲线、曲面是否有交,对相切情况的计算结果进行修 正,可提高奇异情况下的求交稳定性。算法已在清软英泰公司开发的自主版权3维CAD软件GEMS中得到应用。
关键词:曲线曲面求交;坐标变换;拉格朗日乘子法;最小距离

引言中一些总结的话语：Levin[ 1,2] 用隐式多项式方法表达二次曲面,利 用矩阵的代数运算和参数方程求解二次曲面之间的 相交问题,并提出不同坐标系中曲面的表达形式可 通过坐标变换来实现,该方法称为代数法(algeb raic approach)。Miller[ 3~7] 对基本二次曲面(球面、正圆 柱、正圆锥)提出用几何参数(向量、点、标量)表示二次曲面,求解平面与曲面、曲面与曲面之间的相交问题,称为几何法(geometric approach)。Shene和 Johm s tone用几何表示法,研究了退化情况下二次曲 面相交为平面曲线的情况[ 8] 。王新龙等用此方法 分别研究了部分二次曲线、四次曲线与二次曲面的 相交情况9] 。
几何法的优点是计算精度高,但对不 同曲线曲面的相交问题,需要分别处理多种情况,使 得程序流程非常复杂;且不能求解任意位置的曲线 曲面求交问题。代数法表示的优点是可以统一地表 示所要求解的问题,便于编写统一的求交算法,可以 处理任意位置的二次曲面问题,弥补了几何表示法 的不足。但对于一般二次曲线曲面求交,代数法很 难给出解析表达式,需要采用数值方法求解,交叉迭 代是常用的方法。迭代法可以得到曲线曲面交点的 数值解,但存在求解稳定性、求解精度等问题,所以 利用代数方法求解交点的解析解仍然是求交问题的 研究热点。同时,奇异情况(相切和重合)也是在求 交应用中需要特殊处理的问题,常常由于数值求解 精度的限制而导致结果错误。

二次曲线是一个平面曲线。将二次曲线和二次曲面变换到以二次曲线所在平面的局部坐标系下，然后此时局部坐标系下，二次曲线为xoy平面内的曲线，二次曲面与二次曲面有交点必然在xoy平面上，即z坐标=0。
而二次曲面与平面相交，交线最多为二次曲线。是能够解析表达出来的。然后就转化成平面内，两条二次曲线求交的问题。
但是为了避免二次曲线与二次曲线求交点（是一个四次方程求解问题），加入了一个最近距离的计算，来判定是否有交点。文中给出了计算最近距离的方法。然后拿了一个圆和圆锥曲面作为实例。
//但是这个地方有一个疑问，一般情况下，二次曲线和二次曲面的最近距离计算应该也不是一个简单的问题吧？所以这个距离判定不好用？但是对于圆和圆锥曲面的最近距离，由于圆的特殊性、圆锥曲面的特殊性，这个距离比较好计算？？？

文中提到：对于奇异情况下切点的求解会出现有两个实数解或没有实数解的情况，可以取计算结果的平均值作为切点坐标。这样能够提高曲线曲面相切的结果的精度。

评论：将二次曲线和二次曲面的求交转换为二次曲线和二次曲线的求交问题，是一个很好的思路。同时，坐标系变换然后做求交处理也是一个简化计算、提高精度和效率的方法。

（2006年）RCS计算中NURBS曲面和射线求交的快速计算(官火梁 吴强 席平/北航)

摘 要：提出了一种基于牛顿迭代法解方程组的射线和NURBS曲面求交算法。利用预先计算射线和曲面交点个数最大值，通过折中适应性分割曲面得到迭代初始值，达到了快速计算的效果。同时，解决了射线与NURBS曲面多交点判断、自交点筛选等问题，保证 了交点精度，且不会遗漏交点。
关键词：计算机应用；快速计算；牛顿迭代法；射线追踪；NURBS曲面

雷达散射截面计算(RCS 计算，Radar Cross Section) 分为两部分，一部分是射线追踪计算， 另一部分是耦合效应计算。

射线和NURBS曲面控制顶点多域网格 的交点个数为k，射线和NURBS曲面的交点个 数为h，射线和曲面没有重合时，k≥h。//nurbs曲面的特性。//射线和NURBS曲面控 制顶点多域网格的交点个数k很容易求出。因 此，可以预估计射线和曲面交点个数。
并且，如果射线和曲面没有重合时，且k>1，可以不断地通过折中适应性分割曲面，最终一定 能得到所有的叶子节点曲面片对应的k满足k≤ 1。此时，在每个区域内迭代求交，能够保证不漏掉交点。（//如果射线和曲面控制顶点多域网格的 交点个数k等于1，并且起点对应的(u，v)参数在 子曲面片参数域内，应该停止该子曲面片和射线 求交运算。//因为交点就是射线的起点。）

评论：这个充分利用nurbs曲线曲面的凸包交点的个数的特性，是一个不错的思路。可以考虑作为是否继续曲面细分的一个条件。

// Todo

3 曲面曲面

3.1 平面/二次曲面

直接解析法计算交线。

3.2 二次曲面/二次曲面

// Todo

3.3 其他类型

国内

（1995年4月）隐式曲面／参数曲面的求交算法 （冉瑞江 王亚平 唐荣锡/北航飞行器制造工程系）

思路：

• 1.将n次代数曲面方程用齐次坐标的表示；
• 2.将参数曲面用NURBS表示，然后插入重复节点，变成一组有理Bezier曲面，平且改写成齐次幂级数形式；
• 3.将2中的齐次坐标表示代入1中，得到关于参数u、v的方程。（该方程就表示uv参数域的一条平面曲线）；

然后分析讨论平面代数曲线$F(u,v)=0$的性质。

追踪：
在跟踪之前，对于每一个特征初始点，记录其连接次数，即从该点开始或者终止的单调分枝数。

估算下一个点：用切线、或者用密切圆的方法计算近似点
计算精确的下一个点：

注意：一点想法和改进，这个地方需要两次迭代计算两个最近点，会不会是效率降低？
我使用的方法是，直接把当前点作为初始值，放入方程组中迭代，会得到一个精确交点。这样计算次数会不会少一些？但是存在一种可能，就是可能得到的新的点离当前初值点跑了一些距离。不知道本文中用两个最近点的迭代会不会存在这种问题？

文中说到：跟踪时要 注 意 不 要 进 入 交 线 的另一 分枝 和 重 复 跟 踪 同 一 交线分枝， 算 法可 靠性的关键在于适当控制步长和精度 。

// 这和我当时做求交考虑到的不谋而合。

// 这个地方我当时做求交的时候也考虑到了，为了避免这种情况，会在出参数域的时候做一个判断，当跨出参数域的那一刻，与边界计算出精确的交点，并停止继续计算边界外的交点。

（1997年12月）平面向量场与曲率分析在曲面求交中的应用（宁涛 马德昌 王亚平 唐荣锡/北航飞行器制造工程系）

在 曲面 求 交 的 跟 踪 算法 中，主 要 有 三 项关 键 技 术：（1）初 始跟 踪 点集 完 备 性（2） 数 值 方法稳 定 性（3）误差准则一致性。

如果找 到 两 张 曲 面 的所有 共 线法 矢， 沿共线 法 矢 点对 两 曲面 进 行分割，那 么 所得 到 的小曲面 片 没 有交线 环. 这 样 就保 证 了不 遗漏 任何交线 环.

对于相切点的位置追踪方向的计算：

//这个计算方法和我当时做求交的时候，处理相切情况计算切向的方法一样。并且确实可能会出现多解情况，也就是交线会在这个地方出现多个分支。最好根据前一次的跟踪方向，来确定当前走哪个分支，这样计算的交线走向更自然。
跟踪步长的计算方法：

//“ 根据 曲 率估 计 跟 踪步长 是 毫无 意 义 的”。确实如此，在实际工程中，我在估算跟踪步长的时候，虽然通过曲率计算得到估计步长，但还要做其他的限制处理。并且步长的估算公式最好是连续变化的。
对于相切点的位置跟踪步长的计算方法：

// 看起来这个估算曲率的方法也不错。因为曲率本来是用来估算步长的，不需要精确，所以采用本文中的方法似乎是个不错的选择。
// 我做求交采用的是利用更高阶偏微分计算相切点的曲率，计算方法可以从某一篇分析交线的微分的论文中找到。但是采用更高阶偏微分计算曲率计算量比较大，并且不是很稳定，因为可能像nurbs曲面没有连续的更高阶的微分。

曲 面 求 交 的 主 程 序 由三 部分构成：（1）计算 两 张 曲 面 的 包 围 盒，利用包 围盒 进 行求交粗判；（2） 计算 两张 曲 面 形 成的平 面 向 量 场， 用Kriezis方 法 求 出 临界 点。然 后， 利用 曲线/曲 面 求交算 法 计算 初始跟踪点 和 跟踪 方 向。（3）对外部 初 始跟 踪点 和 内 部 初 始 跟 踪 点分别 进行 跟 踪，得到 所有 交 线。外 部初始跟踪点 是 指 至 少在一 张 曲 面 边 界上 的 初 始跟 踪点，内部 初 始 跟 踪点 是指 不 在 任何 一张 曲 面 边界 上 的 初 始跟踪 点.

当跟踪完 所有 外 部 初 始 跟踪 点 后， 所得交线均与曲 面 边 界 有交。如 果此 时 内 部 初 始跟 踪点集非 空， 那 么两 曲 面 有 内部交 线 环。对 内 部 交 线 环的 跟 踪 较 为 简 单， 这 里 不再介 绍。
对外部初始跟踪 点 的 跟 踪 过 程：

// 这里对于外部跟踪点的处理和我当时做求交实现的方法基本一样。
// 或者说其实本文中所描述的求交的理论方法，和我当时在实践中摸索的的实现曲面求交的方法基本完全一致。所以本文很具有实用价值，提到了很多工程实现时的关键问题。

（1995年）曲率分析方法在曲面求交中的应用（宁涛 马德昌 王亚平 唐荣锡/北航飞行器制造工程系）

这篇文章，紧接着上一篇“（1997年12月）平面向量场与曲率分析在曲面求交中的应用（宁涛 马德昌 王亚平 唐荣锡/北航飞行器制造工程系）”。这篇文章主要在讲：相切情况下，切向和跟踪步长的计算方法。里面也提到：
在切平 面 不 重 合的 情 况 下，利 用 曲 面 的 一 阶 导 数 就 能 确 定 跟踪 方 向，但 在切 平 面重 合的 情 况 下， 要确定跟踪 方向 就 必 须使用 曲 面 的 二 阶 导 数， 甚 至 更高 阶 导数。
曲 于 曲率 只 表 示 曲线 在某 一 点处 的 局 部 弯 曲程 度， 所以 对 于 曲率 变 化 大 的 曲线，只 根据 曲率 估 计 跟 踪步长 是 毫无意 义的。然后举了一个例子说明：两 条 空 间位 置 非常“接 近”的 曲 线， 其曲率可 能 相 差 很 大。所 以曲 率相 对 于 空 间位 置 是极 不 稳 定 的量， 仅 用曲率 估 计 步长 不 能 得到稳 定 可靠的 结果。由 于 实 际 中 使 用 的曲 线， 其曲 率变化 一 般 比 较均 匀， 使用 曲 率估计 步 长仍是 一 种 实 用 方 法。但在 算 法 的实 现 中， 一定 要 考虑 到 曲率的不稳定 性。

评论：这篇论文的主要内容在“（1997年12月）平面向量场与曲率分析在曲面求交中的应用”基本都覆盖了。

（1999年3月）一种参数曲面与隐式曲面的求交算法（余正 彭群生 马利庄/浙江大学CAD＆CG）

生成$h(u,v)＝0$的等值线，其主要算法步骤如下：
1） 逐个计算每一网格单元与等值线的交点；
2） 连接该单元与等值线的交点，生成该单元内的一等值线的线段；
3） 由一系列单元内的等值线的线段构成该网格中的等值线．
计算单元的各边与等值线的交点，假设函数 h（ u，v） 在单元内呈线性变化，可以采用顶点判定和边上插值的方法计算交点，具体步骤如下：

图(a)二维标量场抽取参数曲面的参数域的等值线，该等值线在参数曲面上的映射，便得到参数曲面与隐式曲面的交线c，如下图（b）。

评论：对于计算初始点，用网格法，计算h（ u，v）不用迭代也很快，确实不失为一个好方法。但是网格划分的密度是一个问题，划分太密计算量也很巨大，划分太稀可能会漏掉某些初始点（譬如说小环或者孤立点）。

（2000年3月）一种高效的自由曲面求交算法（陈丽萍 姜歌东 王小椿/西安交通大学）

这里提出了一种对于相切情况下，计算曲线和曲面交点的处理方法：“如果没有交点，或者｜Δ1｜存在局部极值，上述算法将在极值点，附近出现零除或发散现象，导致算法失败．”

这篇文章的方法，是将曲面分割成若干个小的面片，然后对每一个面片，计算初始点。计算初始点利用了距离和极值点来判断，并且用迭代法计算曲线曲面的精确交点。
评论：方法可行，但是感觉这种方法的效率应该不会太高。

（2004年）圆环与圆环求交算法中初始点的计算 （王日昀 宁涛 席平 唐荣锡/北航飞行器制造工程系）

在曲面求交方面做了大量的研究并相继推出很多优秀的算法 [1]~[5] 。算法大体上可归为 4 类：
分割法 （subdivision method），网格计算法 (lattice evaluation)，几何法 (geometric method)，追踪法 (marching method)。

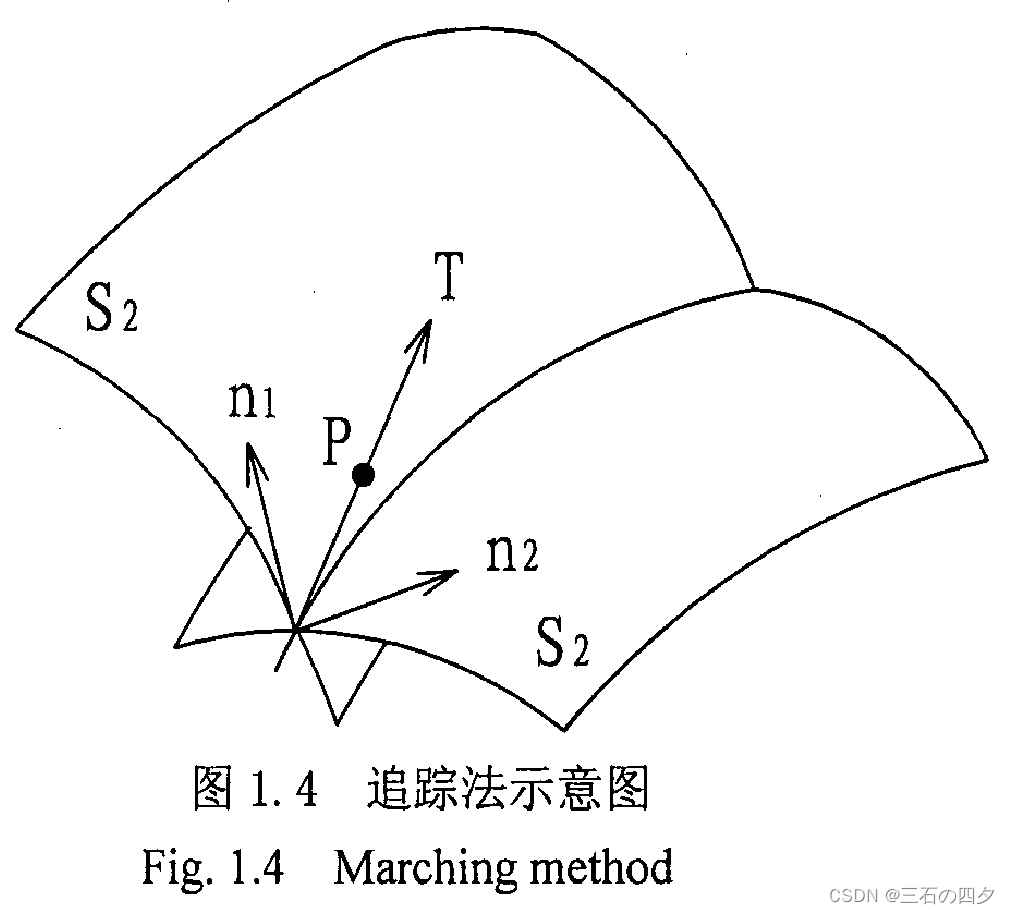
先通过某种求交方法确定各交线环上的一个交点，根据交线的几何性质，按照一定步长计算该条交线上下一交点的近似值，再应用迭代法求得精确的交点。沿交线走向不断前进，直至遍历整条交线。追踪法求交的原理如图 1 所示。

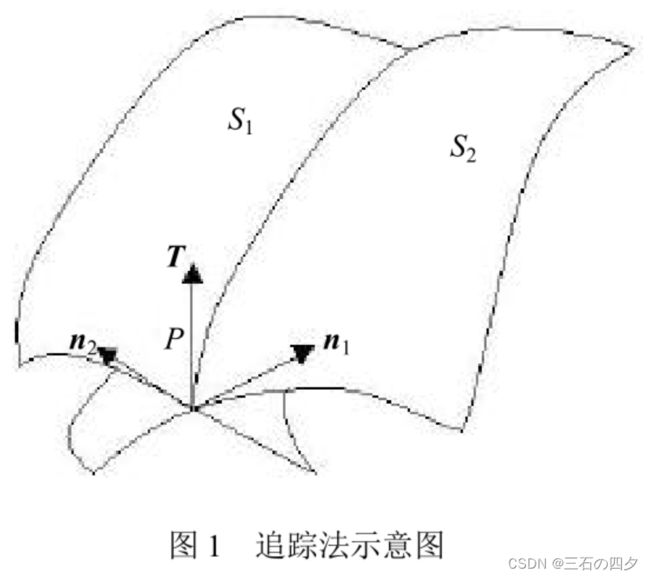
追踪法求交的优点是在求得首交点后搜索交线的其余交点的速度非常快，且适用范围广。参数曲面，只要曲面不存在非正则点，并可以求得曲面上任意点的坐标位置、法矢、切矢等几何信息，就可以用追踪法求交。
缺点：追踪法的问题是目前尚无有效的方法来求得所有交线的初始点。在有些情况下寻求初始点所花费的时间远大于追踪过程所节省的时间，而为了节省寻求初始点的时间，又可能漏掉某些交线，当在孤立交点和比较小的交线环时尤甚。

交线类型分析：
一般曲面相交交线类型包括：开环线，闭环线，尖点，切点。而在圆环与圆环相交中不存在开环线，且尖点也是以切点的形式存在，所以主要任务就是发现所有的切点，并计算出闭环线的初始点。

评论：这个分析方法不是很好，而且会用到了在接近的区域细分，实现起来复杂，性能可能也一般。
我的思路：对于两个圆环面，是否可以考虑第二个圆环面中心圆和内外圆在第一个圆的平面上的投影曲线（二次曲线），然后计算二次曲线之间的交点，估算出大概的相交区域，然后利用附近位置的等参线（截面圆）与另外一个圆环计算交点（作为初始交点），或者在这种区域附近将两个圆环面细分计算初始交点。

（2005年6月）圆环面/球面求交算法 （陈小雕 雍俊海 郑国勤 孙家广/清华计算机科学与技术系）

求交算法在保持拓扑稳定性上仍然存在着两大问题：一是求交分支漏解，二是使用跟踪法时在某些情况下会发生分支跳跃。

本文结合点圆最近距离计算与区间中点测试求交方法［11］提出了统一求解所有三种类型的圆环面/球面求交问题的算法。
（注：球面（球心）与圆环面的最近距离是不是也不难计算？是不是可以利用一下，对求交有帮助？）。正好，论文中也利用了一些方法，计算了球心到圆环面的最小和最大平方距离。

$\Delta ＝l_1^2＋l_2^2＋l_3^2$（6）
其中:
$$\begin{gathered} l_1＝－2r（x_{0}cosu＋y_{0}sinu－R） \\ {l}_2＝－2r{z}_0 \\ {l}_3＝x_0^2＋y_0^2＋z_0^2＋r^2＋R^2－{\delta }^2－2R（x_{0}cosu＋y_{0}sinu） \end{gathered}$$

若$l_1$,$l_2$ 全为0，则圆 U 在球面上或者与球面无交；否则Δ的符号与圆U 和球面的相异交点的个数有如下关系:
Δ＞0有两个相异交点
Δ＝0有一个相异交点
Δ＜0没有交点

式（6） 对交曲线的拓扑结构分析来说很重要，故称它为关键方程。

圆环面和球面最多只有两条交线？？？？

评论：很有效的方法，可以实际中实现用起来。

（2007年）采用“结式法”的圆环面和球面求交算法（谌炎辉 徐武彬/广西工学院机械系）

讨论圆环面小圆和球面截圆(指球面在XOZ平面上所截的圆)的位置关系给出了圆环面和球面不相交、交线为圆、交线为孤立点、交线中自交点和尖点及交线的区间等。

评论：这篇文章与上一篇文章基本相似，只不过讲述的偏几何一点（上一篇更偏代数），更容易理解一点。

思路：可用如下两个方向的投影快速判断有没有交和交的大概位置。

毕业论文

（2001年1月）实用曲面求交算法的研究与实现（渠建平/北京工业大学）

前人的方法总结如下：
基于分割的求交算法：
分割求交分三步进行 分割、求交和交线组织。分割是将一张曲面片分割成四张小曲面片，分割方法主要取决于曲面片的 表示和性质。在分割的同时，要不断比较两曲面片的凸包，以判定它们是否相 交，如果相交则继续分割，直到小曲面片在指定的精度范围内近似于平面。经 过分割，形成一系列有交的近似于平面的小平面对。求交过程是先对这些小曲 面片对用四边形或两个三角形近似，再计算多边形之间的交线，并认为该交线 就是小曲面片对的近似交线。到交线组织时，将这些交线段连起来，形成整个 曲面的交线。
1）曲面形式的转化：有理或非有理Bezier曲面有很好的分割性 质。工程实际中多用B样条和NURBS及其它各种形式表示的曲面，因此，首先需将所给曲面转化为有理或非有理Bezier的曲面形式。
2）相交性测试：包围盒加速。
3）平坦性测试：自适应分割是通过在分割过程中检查曲面 片的平坦度的方法来决定是继续分割还是以小曲面片近似求交。其中，平坦度定义：Barnhill于1990年给出了另一种平坦性确定方法， 即以曲面片四个角点和中心点的切矢及法矢来确定。但平坦度的容许值（$<\epsilon$）怎样选取，不是凭主观随意所能确定的，这里涉及到运算的累计误差和计算机浮 点运算的截断误差。
4) 分割：自适应分割则与平坦性测试有关，它与等深度分割相比，分割量小、占用 内存少，因而具有速度快、同样交线表示精度所需的交点数目少等优点。
5） 求交及交线组织当分割到一定深度时，认为足够平坦的两冲突曲面片之 间可以用四边形或两个三角形近似求交，得到的交线段依照区域的连贯性连接起来。
基于数值迭代的求交算法
数值迭代本身来说，不能算是一种求交算法，它只是对近似交点的求精 过程，即把近似交点逐步迭代到曲面的真正交线上。//这个只属于跟踪法中的迭代求精的方法。
基于跟踪的曲面求交算法
搜索 初始交点 的方法：
第一种方法是用一张曲面上 的等参数网格曲线与另一曲面求交，求得一组交点。使用这种方法时，为了避 免漏交，往往须加密网格线。
第二种方法是把两张曲面都递归分割成四叉树结构。先把整张曲面分割成 张子曲面片，如图 所示，如果子曲面片不满足某种平坦性要求，就把它 分割成 张更小的子曲面片。如此递归检测与分割，形成一棵四叉树，其叶子 结点对应的子曲面片都满足平坦性要求。每一个结点都可生成一个包围盒，包 含该结点所代表的子曲面片，然后对两个包围盒树求交，若某个叶子结点与另 一张曲面的某叶子结点有交，则把对应的各子曲面片的平均参数值作为近似参 数值，对应曲面上的两点的中点作为近似交点坐标，并用求精迭代方法进一步 精确化。
Lattice网格离散法
该方法与分割法类似，基本思想是先将两曲面离散为 由小曲面片组成的网格形式，当网格分得足够细密时，可以认为已经非常接近 真实曲面。将两张分别表示不同曲面的网格利用平面片求交法求得交线，并以 此近似代表曲面间的交线。这种方法原理简单、容易实现、适用范围广。缺点 是精度不高、而且占用内存大、速度较慢。
解析法
一般的做法是先将曲面表示 或转换 为代数方程形式，并利用求解高次非线性方程组求得交线。只适用于低次曲面或多项式曲面的求交问题。
三角剖分求交法
适用于离散造型的一种方法。按照一定的规则把曲面剖 分成三角网格形式，利用三角面片求交法求得交线。优点是速度快、稳定性强， 但精度不够。

本文的方法：
二分跟踪法的求交
NURBS曲面由推广张量积曲面形式得到，然而， 一般地，一张NURBS曲面不是一张量积曲面。//带权控 制顶点在高一维空间里定义了一张量积的非有理 样条曲面 。
1）NURBS曲面的分片：该定义域被其内节点划分成$(m-p+1)x(n-q+1)$个子矩形。NURBS曲面是一种特殊形式的分片有理参数多项式曲面。上面所述的特殊形式的分片是必须的，可以称之为一次分割，在此基础上 再进行二次分割，即这里所讲的“二分” 。 ///在参数域[0.1]上把曲面分割成两部分，而不是四部分或更多。//二分的优点：空间复杂度明显降低。因为该方法采用的是二叉树数据结构，因此在空间复杂度 即占用内存 上明显降低，比四叉树数据结构在空间效率上提高一倍 。时间复杂度也明显降低。采用二分原理，在时间复杂度即运算复杂度上，比通常的四叉树方法提高 了几个数量级，因为采用二叉树数据结构，数据运算量比四叉树减少一半；并且不进行平坦性测试，使运算量减少了若干倍。

自由曲面与自由曲面求交
两二次参数曲面求交，交线次数为64次，两个三次参数曲面求交，交线次数高达324次。
二分跟踪法的实现
采用四阶变步长龙格——库塔法。

卡什一卡普内嵌法龙格—库塔公式。卡什一卡普的5阶内嵌式龙格——库塔法。

二分跟踪法的应用
曲面裁剪、曲面过渡。
其中曲面过渡中提到：参数方程方法，一种是以球面族包 络面方程作为过渡面数学模型来生成过渡面，这种方法需要大量的导数运算， 比较繁琐；另一种利用球面族包络面法截线上矢量共面的线性关系，通过u，v参数的曲面映射，推导出球心的轨迹线、接触线和过渡曲面的方程。本文由于采用了生成过渡曲面的算法中采用等半径圆球包络面作为相交曲面的过渡面，方 法简单，速度快。该算法里的核心算法还是曲面求交算法。

（2007年12月）基于层次包围盒的Bezier曲面求交算法研究及实现（姚薇薇/大连理工大学）

本文充分利用Bezie:曲面的凸包性和易于分割的优势，在曲面分割求交算法和层次包围盒的碰撞检测基础上，研究了Bezie:曲面求交算法。使用两种层次包围盒:轴向包围盒(AABB)和方向包围盒(OBB)提高求交算法相交测试的效率，并比较了在两种层次包围盒的情况下，算法的稳定性和效率。
利用Bezier曲面的德卡斯特里奥算法及四叉树数据结构对曲面进行递归分割。取前次分割得到子曲面的控制点来构建层次包围盒。利用层次包围盒间的碰撞检测对有交的子曲面进行的相交测试。将测试结果为相交的子曲面离散化为三角面片，利用三角形/三角形相交测试求出交点。对于交点用B样条曲线进行优化，得出最后精确交线。并在曲面等深度分割和自适应分割两种情况下，对轴向包围盒(AABB)和方向包围盒(OBB)两种层次包围盒进行比较。得出应用轴向层次包围盒(OBB)进行Bezie:曲面求交，更能满足求交算法高效、稳定的要求。

曲面求交的基本数学类型
代数/代数曲面求交：两曲面的显式方程；
代数/参数曲面求交：一张以代数方程中隐式方程，另一张曲面以参数形式表示；
参数/参数曲面求交。

参数/参致曲面求交的基本方法：解析法(Analytics)、网格离散法(Lattice)、几何分割法(Geometric division)、代数迭代法(Algebraic iteration、跟踪法(Trace)等。

1. 解析法：通常是将参数/参数求交问题转化为代数/代数曲面或代数/参数曲面求交问题(见上述代数/代数曲面求交)，并利用求解一元高次方程得到交线。//这种方法在计算低幂次(二次以下)曲面片间的交线时可以获得较好的效果。三次以上的自由曲面，特别是有理曲面的求交，交线代数方程的阶数将非常高。例如，一张双三次曲面片转化的代数方程为一含有324项的18次方程。采用代数法对两张双三次曲面片求交，交线方程为324次。
2. 网格离散法：该法的基本思想是先将曲面离散为由小平面片组成的网格，当网格足够细密时，可以认为己经非常接近真实曲面。
3. 分割法：分割法与网格离散法有些类似，都是以小平面片的交线代替曲面的交线。所不同的是分割法不是将曲面直接离散，而是基于分而治之的思想，即在对两曲面片离散之前，先利用曲面片的凸包进行相交测试，并只对凸包相交的曲面片进行细分。分割求交的精度比较低，分割法也需要与其它方法结合才能获得比较满意的效果。（离散策略的选择：由于bezier曲面有很好的分割性质,de Casteljau算法进行曲面分割即只需要对曲面的控制顶点集分割就能很方便地将整个曲面分成四个独立的曲面片。对曲面求交时,是利用曲面本身进行离散分隔求交还是将曲面转化为有理曲面的形式再求交。分割深度的控制：分割求交中比较常用的是等深度分割和自适应分割两种方法。自适应是指在分割过程中同时检查曲面片的平 坦度来决定是否需要继续分割。自适应分割则与平坦性测试有关。平坦性测试((Flatility Test):自适应分割是通过在分割过程中检查曲面片的平坦度的方法来决定是继续分割还是以小曲面片近似求交。一般来说，可以曲面片凸包的厚度与凸包底面的面积之比作为平坦度。Barnhill于1990年给出了另一种平坦性确定方法，即以曲面片四个角点和中心点的切矢及法矢来确定。相交性((Conflicting)测试:Bezier曲面片的凸包性能够使曲面完全被包容在由控制点形成的凸包内。利用凸包性来判断相交的可能性。//注：这个地方可以考虑用OBB包围盒，计算OBB的方法可参考前面某篇文章。）
4. 迭代法： 迭代法只能算为一种数值方法，其本身并不能构成一个独立的求交方法。与所有不动点迭代法一样，应用迭代法求交线之前，首先必须给出交点的初始估计值，而交点的初始估计值必须通过其它求交方法得到。因此，迭代求交法常同其它求交方法结合使用，
   作为交点精化的一种手段。
5. 追踪法：在己知某一点为两曲面交点的前提下，以该点为起点，沿着交线前进方向搜索下一个交点;重复上述的过程，直至求得交线上的所有交点。该法的优点是适用范围广，可用于任意参数曲面，而且计算速度快。占用内存少。追踪法的关键是初始点的获得比较困难。

当曲面间存在切点时，由于在切点附近两曲面的法矢非常接近。认为在此时应该停止追踪，并从另一个方向重新进行追踪，直到切点附近再停止。// 这是一个不错的思路，对于迭代到相切点，也可以停止迭代，从另一方向开始迭代。

运用层次包围盒方法进行碰撞检测时，如果包围盒不相交，则物体肯定不相交。只有包围盒相交时，才对其所包裹的基本几何元素做进一步相交测试。即:首先判断两包围盒树的根结点是否相交，如相交则进一步判断它们的子结点相交情况，如最后有相交的叶结点对，判断每对叶结点包围的基本几何对象是否相交。层次包围盒是一种基于包围盒层次的树状结构，有长方形包围盒、球形包围盒等。

从层次包围盒构造方法可以看出，像AABB球形包围盒虽然构造简单，但包围盒彼此之间存在大量的重叠情况，因而测试的次数相对较高。而OBB和凸多面体包围盒虽然构造过程复杂，但紧密性较AABB和球形为高，因而测试的次数相对较小。碰撞检测的时间效率与包围盒紧密性和应用对象有很大的关系，在应用上应根据应用对象和环境的不同，选用不同的方法。

当包围盒A, B在三条轴向上的投影均相交时，则A, B相交。因此AABB间的相交测试最多只需6次比较运算。

OBB的创建方法：协方差矩阵C计算，协方差矩阵的3个特征向量正交。求出这3个特征向量。将3个特征向量正规化作为基底，确定OBB的3个方向。// 也可以利用bezier的控制顶点，简单计算一个OBB包围盒。

OBB包围盒树分裂：确定分裂轴，使用最长轴剖分方法(如图3. 7所示)，即:选择包围盒的最长轴作分裂轴，选用垂直于该轴的平面来剖分OBB包围盒，若最长轴无法剖分，则选用次长轴，若次长轴仍无法剖分，则选用最短轴，若仍无法剖分，则包围盒中的形体定义为不可分，作为OBB树的叶子结点。确定分裂点，定位分裂平面(使用中值方法)。剖分的位置选为包围盒中所有顶点的均值位置，即选用OBB包围盒的中心(顶点分布的均值件)，应用基于分裂平面的划分方法将所有OBB的元素分为两个子集。

OBB间的重叠测试：分离轴原理： 定义:对于直线L，如果凸多面体A, B垂直投影到L上的区域不相交，那么直线L就称为凸多面体A,B的分离轴(Separating Axis )。//如果分离轴存在，则必定有一个分离轴符合下面三个条件之一:垂直于A的某个面;b，垂直于B的某个面;。，垂直于一个平面，该平面平行于A的一条边和B的一条边。因此，两个OBB间只要存在一条分离轴，就可以断定其不相交。对于一对OBB
来说，共有6个面方向，6个边方向，因此共有$C_6^2=15$个可能的分离轴。逐个进行判断，当可以确定某个轴为分离轴时，即可停止计算。因此最多共进行15次比较运算。

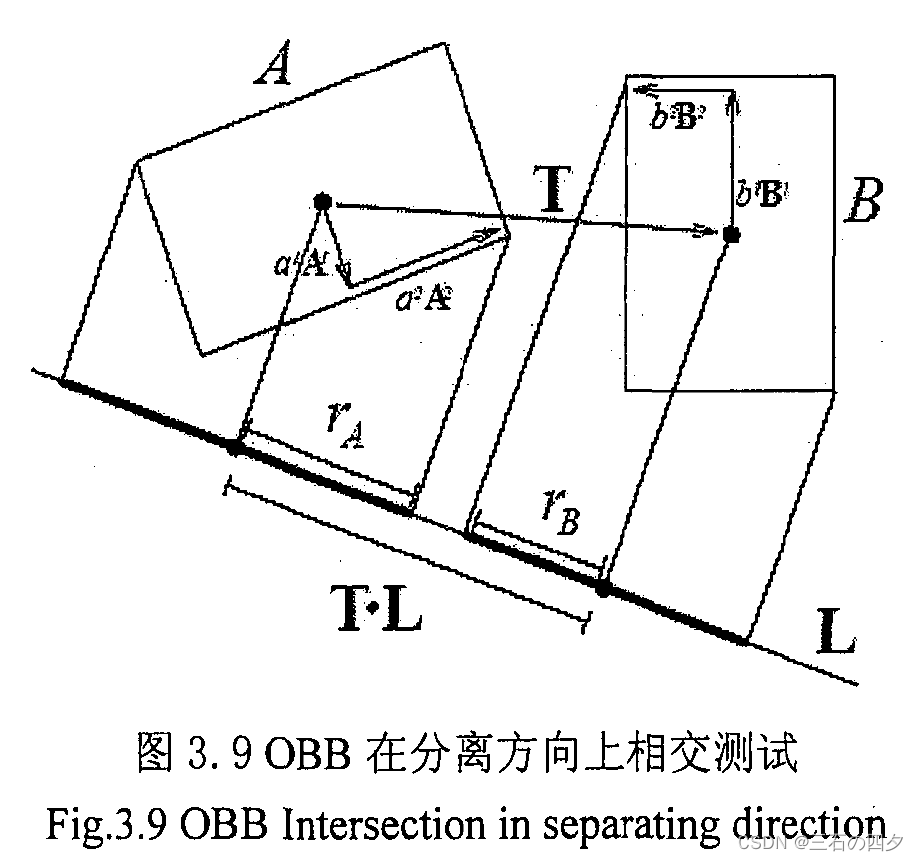
首先将两个oBB包围盒的中心投影到轴上，然后计算投影间隔的“半径”。如果两个OBB包围盒的中心间距的投影大于“半径”之和，那么两个OBB包围盒分离(如图3.9所示)。

三角形和三角形相交测试方法
Moller提出。每个三角形是其所在平面的子集，如果两个三角形相交(三维时的情况)，其必与两个平面的交线相交。由此可知，三角形对相交的必要条件是每个三角形必须与另一个三角形所在平面相交。因此，要判断两个三角形是否相交，可首先检测每个三角形是否与另一个三角形所在的平面相交，根据检测的结果再做进一步的测试。

基于层次包围盒的Bezier曲面求交算法
四叉树每个节点的孩子节点数量比二叉树增加一倍，树的高度约为二叉树的一半，需要更新的节点数更少和总的更新代价降低，所以在包围盒重叠测试中四叉树明显比二叉树快。

曲面片被分割到一定深度后，其子曲面片已经达到平坦度要求。有建议以子片面的四个角点构造双一次曲面，运用代数法求得两张双一次曲面片，运用代数法求得两张双一次曲面片的交线，近似代表原曲面的交线。(该方法的优点是精度比较高，可以在比较低的分割层次下获得比较精确的交点，但算法的稳定性差，比较复杂。)而常用的是使用两个三角形来代替分割到规定深度的子面片，用一对三角形中的一个与另一对中的两个分别求交线，用得出的交线近似代表曲面片间的交线。

OBBs和AABB测试结果对比分析
OBBs和AABBs在同一个结构中构造。AABB构造方法简单，但oBB的包裹紧密性更优，对于相同的一组控制点多边形网格，构造的两种包围盒的示意图，OBB紧密性的优势很明显。

曲面摆放在原始位置和将曲面对旋转后，AABB的参加测试的包围盒对数差异比较大，而OBB的变化差异较小，说明对于任意空间位置的曲面求交，用OBB包围盒比AABB包围盒百稳定。

由表5.4, 5.5数据可知，在分割层次相同时，oBB参加测试的包围盒对数明显少于AABB;随着分割层次的增加这种差异越来越大。例如在分割层次均为8时，OBB参加测试的包围盒对数为731979，而AABB参加测试的包围盒对数高达8302270。证明OBB的相交测试效率要优于AABB包围盒。

// 评论与备注：虽然说，这篇文章得出了结论，obb相交测试效率比aabb好。但是他测试的是相交包围盒的对数。而实际上，要考虑到obb和aabb包围盒的计算效率，obb比aabb包围盒可能慢一倍？？所以这个地方效率问题，建议还是需要读者测测实际求交所花的时间来对比论证一下。我看这些数据，感觉极有可能aabb的实际效率要高一些？？

文末也提到：由于OBB的碰撞检测比较复杂，所以检测的速度较慢，最好能减少需要OBB碰撞检测的对数。
并提出一个思路：将碰撞检测系统设计为两级碰撞检测系统一Sphere-OBB检测系统，第一级碰撞检测将通过基于Sphere包围算法快速发现曲面的可能相交部分，然后将第一级碰撞检测的结果送到第二级碰撞检测系统，进行基于OBB的详细的碰撞。

对于球体来说，有以下两个明显的优点: (1)球体在任何方向上来说都是一个完美的包围体，因为球的对称性，旋转对于球来说没什么变化，仅剩下平移运动的影响。(2)相交测试过程非常的简单而且速度很快。可以首先计算计算出两个球体球心之间的距离，如果这个距离大于两个球体的半径之和，那么不需要做第二层的精确的碰撞检测算法;否则，两者相交，进行第二层的精确的碰撞检测算法。

国外

（1993年1月）Surface-to-Surface Intersections（Nicholas M. Patrikalakis，T. Maekawa, K. H. Ko，H. Mukundan /麻省理工大学，横滨国立大学）

摘要：本文概述了曲面交点问题，重点讨论了有理多项式参数曲面和有理多项式参数曲面的交点情况，包括横向交点和切线交点。重点介绍了行进方法，并讨论了传统跟踪算法存在的问题。本文概述并举例说明了一种使用经过验证的区间常微分方程系统求解器的方法，该方法在鲁棒性方面优于传统的推进方案。
Keywords: rounded interval arithmetic, boundary representation, parametric surfaces, singularity, tangency.

在研究交点问题时，我们所考虑的曲线曲面类型主要可以分为两类:(1) Rational polynomial parametric (RPP)有理多项式参数and (2) Implicit algebraic (IA)隐式代数)。非均匀有理B-样条(NURBS)曲线和曲面可以细分为RPP曲线和曲面，并以类似的方式进行分析。

Depending on the surfaces involved in intersection, we have three distinct classes: IA/IA, RPP/IA and RPP/RPP.
IA/IA Surface Intersection
RPP/IA Surface Intersection
RPP/RPP Surface Intersection：three nonlinear polynomial equations in four unknowns. This is an underconstrained system.

There are three major techniques for solving RPP/RPP surface intersections: lattice methods, subdivision methods and marching methods. Detailed reviews can be found in [29,31,30].
we focus on marching methods which are efficient in most cases and hence attractive if combined with other methods such as adaptive subdivision methods to locate starting points.//结合追踪法和其他方法（自适应细分方法，用来找初始点）。

计算初始点
为了识别交点曲线的所有连通分量，可以定义交点曲线上的一组特征点。这样的集合可以包括交点的边界点、转弯点和奇点，并在任何连通的交点段上提供至少一个点，并标识所有奇点。
Collinear normal points provide points inside all intersection loops and all singular points [12].

To compute border points, a piecewise rational polynomial curve to piecewise rational polynomial surface intersection capability is required。
Now we split the patches in (at least) one parametric direction at these collinear normal points.//利用好共向法线点。

两个曲面相切的交点：由于交点上两个曲面的法向量相同，因此在交点曲线C’(s)方向上，两个曲面在该点处的法曲率相同。这意味着两个曲面的第二个基本形式是相等的。可以利用这个条件构造方程，求解计算出此时交线的切向。

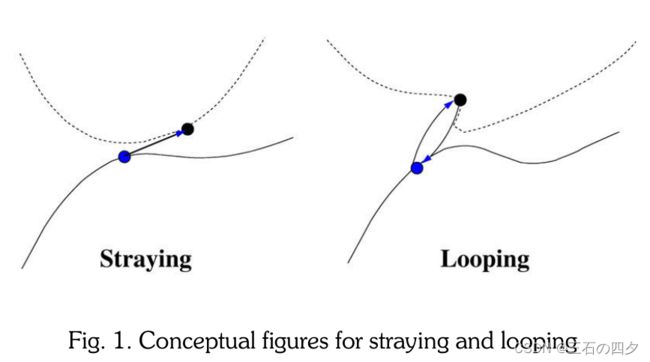
when two intersection curves are close to each other, then step size selection becomes complex and incorrect step size may lead to a critical problem, straying or looping [6], which is illustrated in Figure 1 [27].

the system of equations (6) is provided as input to a Matlab ODE solver, ode45, which is based on the Runge-Kutta method and adopts an adaptive step size control scheme. As Figure 2 shows, the Matlab ODE solver breaks down near the singular point.

追踪稳定性的处理
To ensure robustness in finding roots of the ODE system, researchers have focused on validated schemes using interval arithmetic [26]. The validated ODE solution scheme traces a solution after verifying the existence and uniqueness of the solution at every step.
After validation, a bound is computed which encloses errors in initial values, truncation errors and round off errors [4].

实际实现时：A validated ODE solving scheme consists of two phases [28]: Algorithm I and Algorithm II.：
Algorithm I finds an a priori enclosure and a step size (based on validation) such that the existence and uniqueness within the a priori enclosure for the step size is verified. This validation is achieved by applying Picard-Lindelöf operator and Banach’s fixed point theorem [28].
Algorithm II deals with the propagation of the solution, reduction of wrapping and further prediction of a new step size for the next step.

文献27详细介绍了一些验证处理方法：处理追踪过程中可能出现的错误情况。提升稳定性。// [27] H. Mukundan, K. H. Ko, T. Maekawa, T. Sakkalis, and N. M. Patrikalakis. Surface intersections with validated error bounds. Technical Report 2003-6, Design Laboratory, MIT, 2003.

// 评论：重读Patrikalakis这篇求交文献，感觉到大佬对于求交这方面所作研究的深刻。说多了都是废话，就是两个字，敬佩。这篇文章，对于初始点计算没有给出详细的方法（但是给出了很多方法的参考文献），但是对于追踪过程中，求交稳定性提供的思路、方案、以及文献参考，绝对是至关重要的。

（1976）Levin J∙A parametric algorithmfor drawing pictures of solid ob-jects composed of quadric surfaces ［J］∙Communications of the ACM‚1976‚19（10）

（1995）Miller J ‚Goldman R∙Geometric algorithms for detecting and calculating all conic sections in theintersection of any t wo natural quadric surfaces ［J］∙Graphical Models and I mage Processing ‚1995‚57（1） ：55～66

（1989）Peigl L∙Constructive method of intersecting natural quadrics representedin tri mmed surface for m ［J］∙Computer-Aided De-sign ‚1989‚21（4） ：201～212

（1983）Sarraga R∙Algebraic methods for intersections of quadric sur-faces in GMSOLI D［J］∙Computer Vision ‚Graphics and I mage Processing ‚1983‚22（2） ：222～238

（1998）Ki m K‚Ki m M S∙Torus/sphereintersection based on a configu-ration space approach ［J］∙Graphical Models and I mage Process-ing ‚1998‚60（1） ：77～92

（1998）Zuo Zheng∙Intersection ‚classification and application of geo-metric modeling ［ D］∙Beijing ：Tsinghua University ‚1998（in Chinese）（ 左　 征∙几何造型中的求交分类及其应用［ 博士学位论文］∙北京：清华大学‚1998）

等

//Todo
// 未完，更新中

注

注：1.若有写的不当之处还请谅解并指正。2.以上论文标题即为出处引用，后面就不再单独做详细的文献引用。