铁路轨道不平顺数据分析与预测
铁路轨道不平顺数据分析与预测
1.引言
铁路轨道作为铁行车的基础设施,是铁路线路的重要组成部分。随着经济和交通运输业的发展,我国的铁路运输正朝着高速和重载方向迅速发展,与此同时,轨道结构承受来自列车荷载、运行速度的冲击和列车的振动等各方面的作用力不断增大,不仅加速了铁路轨道设备的损坏,由此产生的轨道不平顺问题会严重影响车辆行,乘客的舒适度以及设备的使用寿命等,存在非常严重的安全隐患。
在铁路运营过程中,轨道在列车不稳定荷载的反复作用下容易发生一定的几何形变,这其中有些是垂直向和横向的动态弹性变形,有些则是永久变形,而这些现象都统称为轨道不平顺
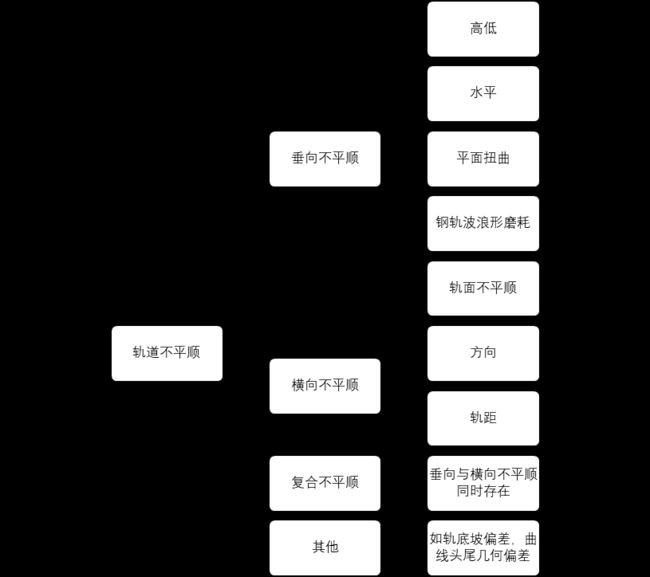
轨道的不平顺会引起列车的振动和轮轨作用力不断变化,不仅影响列车的舒适度,降低轨道与列车部件的使用寿命,甚至可能导致列车脱轨,严重威胁行车安全。其中,轨道的高低不平顺容易激起列车的垂向振动,导致轮轨间作用力大幅减小,甚至造成轮轨分离,使得列车存在悬浮和脱轨的危险。
本项目需要对高速铁路实际运营过程中测量的动检数据进行分析,得到滑动轨道质量指数TQI。进行高低不平顺劣化预测,根据预测结果对模型的预测效果进行评价。
项目目标:
1.分析所给轨道动检数据的滑动轨道质量指数,并结合相应规范给出轨道质量验收报告。
2.根据计算得到的高低不平顺标准差,构建时间序列预测分析模型,预测未来一年的高低不平顺劣化趋势,并采用均方误差和均方根误差对预测模型的结果进行评价。
2.数据预处理
使用python中的pandas库函数读入数据,并对数据进行初步的处理。
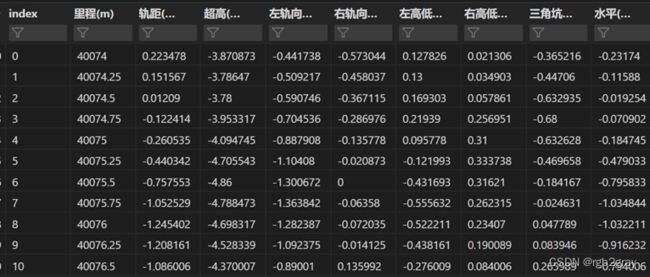
对于2016年1月至2021年12月共计12个月的月度数据读取至dataframe结构,如图2.1所示,一共有:里程(m),轨距(mm),超高(mm),左轨向(mm),右轨向(mm),左高低(mm),右高低(mm),三角坑(mm),水平(mm)共计9个属性。
画出数据分布的箱线图,使用箱线图判断是否存在在可信范围之外的异常数据。箱形图(Box-plot)又称箱线图,是一种表征一组数据分散情况的统计图,主要用于体现原始数据分布的特征,还可以进行多组数据分布特征的比较。箱形图包括最小值(min),下四分位数(Q1),中位数(Xm),上四分位数(Q3)和最大值(max);如图 3-2 所示,绿色矩形框的上下两端边的位置分别对应数据的上、下四分位数(Q3、Q1);矩形框内部的蓝色线段为中位线对应中位数(Xm)。上四分位数与下四分位数之间的距离是数据分布的一种简单度量,它给出被数据的中间一半所覆盖的范围。该距离称为四分位数极差(IQR)。
因此,最大值(max)定义为 Q3+1.5IQR;最小值(min)定义为 Q3-1.5IQR。基于此,视大于最大值(max)或小于最小值(min)的数据为离群点。
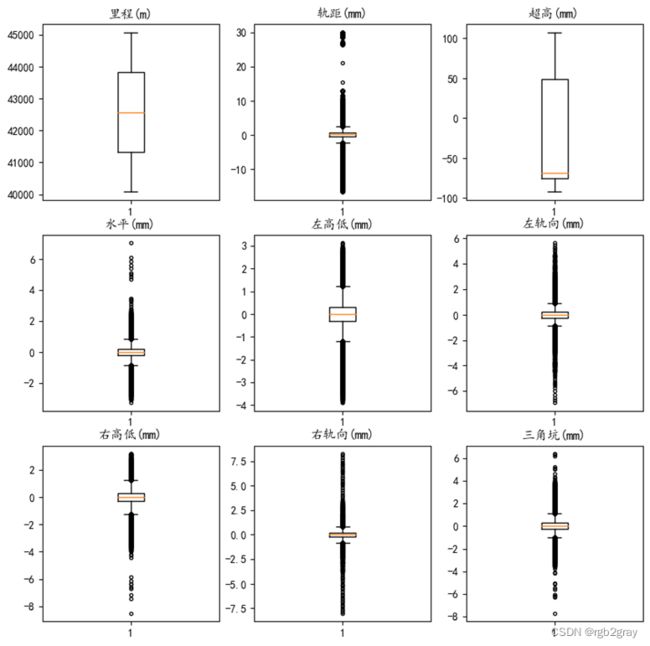
图2.2 数据箱线图
由图2.2可以观察到,数据的轨距,水平,左高低等属性存在较多的离群点即异常数据,这里采用最大最小值异常值替换的方式进行异常值处理。处理之后的箱线图如图2.3所示,所有数据都在可信范围之内。
3.滑动TQI的计算
轨道质量指数是评价单元区段整体不平顺的重要指标。目前,我国釆用的计算方法,主要是通过计算200米单元区段内轨距,左右高低,左右轨向,水平超高以及三角坑等共7个单项的不平顺幅值标准差之和来获得的,能综合反映该区段的整体不平顺状态以及轨道恶化程度。通过对所有轨道单元区段的TQI数值排序可以确定需要重点维修的区段,所以TQI是我国铁路工务部门指导线路维修最重要的指标。
根据工务部门多年的管理经验表明,对轨道区段TQI进行长期的监测和分析,有利于现场维修人员及时掌握轨道状态的改善或者恶化情况以及未来的发展趋势,从而更有效率的编制维修计划。
TQI 以 200 m 长度轨道区段作为计量单元,对单元区段内的轨道几何进行统计,用标准差来表示单 项轨道几何不平顺状态,而 TQI 则为一个单元区段内左高低、右高低、左轨向、右轨向、轨距、水平和 三角坑等七个单项几何不平顺标准差之和,计算方法如下列公式:

由上述TQI的定义,可以得到滑动TQI的计算方法。以1为滑动TQI的移动步长,以800为滑动TQI的移动窗长。以2016年1月的测量数据为例,可以得到滑动TQI结果图见图3.1:
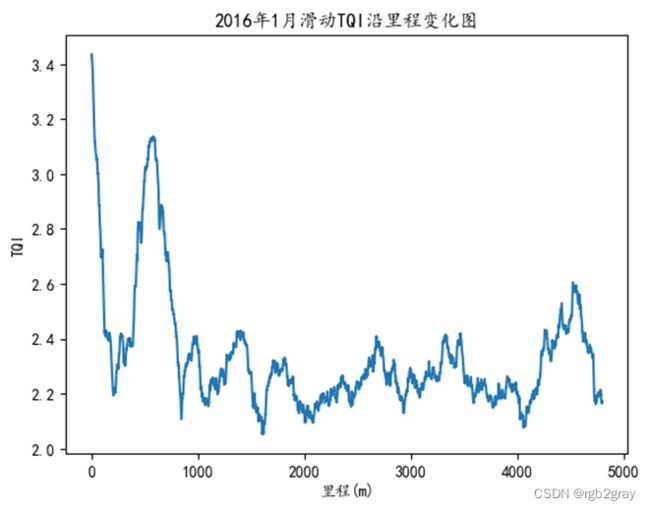
画出2020年1月的TQI沿里程变化图与2016年1月滑动TQI沿里程变化图作比较:
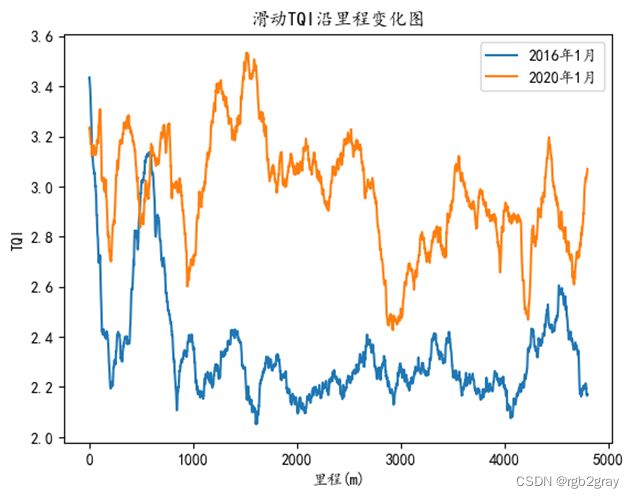
由图3.2可以得出,从2016年至2020年,轨道的区段的状态发生了明显恶化,且在部分区段恶化非常显著。
4.高低不平顺劣化预测
在列车运行的过程中,因轨道不平顺而产生的列车振动加速度对货车以及客车的运行均有影响,主要的影响货车的安全性,客车的舒适性等。由于近年来铁路大面积提高运行效率,朝着高速和重载方向的发展,对轨道结构提出了更高的要求,除了应该具备必要的强度外,还要保持良好的几何形位。为此国内外铁路部门及研究机构都加强了对轨道几何变形的检测。
轨道几何不平顺的变化特征是轨道上大量样本检测点的几何不平顺随时间及车俩载荷重复作用下,表现出共有或者相似的特征,反映了轨道几何不平顺的一般规律。本章采用SARIMA模型进行轨道高低不平顺劣化预测。
我们以K44+074段的左高低为例进行研究,首先画出K44+074段的左高低标准差在2016年1月至2020年12月的变化趋势如图所示:
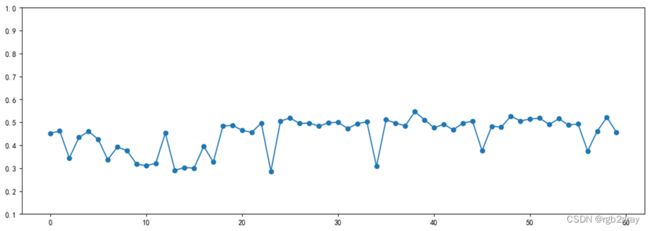
我们选取2016年1月至2019年12月的数据作为训练集,2020年全年的数据作为验证集,使用SARIMA模型进行建立预测模型。
得到ACF与PACF图像如图所示:

由图4.1可知,最佳的SARIMA模型为SARIMA (0, 1, 1)。
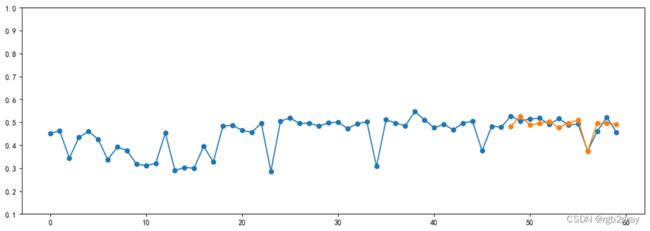
使用SARIMA(0, 1, 1)模型对2020年轨道高低不平顺标准差进行预测可以得到结果如所示:
参考代码:
135. TQI=[]
136. for i in range(0,len(data1)-800):
137. temp_data=data.loc[data.index[i:i+800]]
138. a1=np.array(temp_data['三角坑(mm)'])
139. a2=np.array(temp_data['右轨向(mm)'])
140. a3=np.array(temp_data['右高低(mm)'])
141. a4=np.array(temp_data['左轨向(mm)'])
142. a5=np.array(temp_data['左高低(mm)'])
143. a6=np.array(temp_data['轨距(mm)'])
144. a7=np.array(temp_data['水平(mm)'])
145. re=a1.std()+a2.std()+a3.std()+a4.std()+a5.std()+a6.std()+a7.std()
146. TQI.append(re)
147. import matplotlib.pyplot as plt
148. import numpy as np
149. import matplotlib
150. matplotlib.rc("font",family='KaiTi')
151.
152. x=np.arange(0,4800,0.25)
153.
154. plt.title("2016年1月滑动TQI沿里程变化图")
155. plt.xlabel("里程(m)")
156. plt.ylabel("TQI")
157.
158. plt.plot(x,TQI)
159.
160. # 2020年1月滑动TQI沿里程变化的序列数据
161. TQI_2=[]
162. for i in range(len(data1)*48,len(data1)*49-800):
163. temp_data=data.loc[data.index[i:i+800]]
164. # python中对于矩阵的计算尽量不要在DataFrame中,效率非常低。应该使用numpy
165. a1=np.array(temp_data['三角坑(mm)'])
166. a2=np.array(temp_data['右轨向(mm)'])
167. a3=np.array(temp_data['右高低(mm)'])
168. a4=np.array(temp_data['左轨向(mm)'])
169. a5=np.array(temp_data['左高低(mm)'])
170. a6=np.array(temp_data['轨距(mm)'])
171. a7=np.array(temp_data['水平(mm)'])
172. re=a1.std()+a2.std()+a3.std()+a4.std()+a5.std()+a6.std()+a7.std()
173. TQI_2.append(re)
174.
175. x=np.arange(0,4800,0.25)
176.
177.
178.
179. plt.plot(x,TQI,label='2016年1月')
180. plt.plot(x,TQI_2,label='2020年1月')
181.
182. plt.title("滑动TQI沿里程变化图")
183. plt.xlabel("里程(m)")
184. plt.ylabel("TQI")
185. plt.legend()
186.
187. input_data=[]
188. for i in range(72):
189. temp_data=data.loc[data.index[len(data1)*i+16000:len(data1)*i+20000]]
190. temp=np.array(temp_data['左高低(mm)'])
191. input_data.append(temp.std())
192.
193. from matplotlib.pyplot import MultipleLocator
194. #从pyplot导入MultipleLocator类,这个类用于设置刻度间隔
195.
196. fig = plt.figure(figsize=(15,5)) # 设置画布大小
197. plt.ylim(0.1,1) # y轴显示范围
198. plt.plot(input_data[0:60],'o-')
199.
200. from statsmodels.graphics.tsaplots import plot_acf, plot_pacf # 画图定阶
201.
202. def draw_acf(data):
203. # 利用ACF判断模型阶数
204. plot_acf(data)
205. plt.title("序列自相关图(ACF)")
206. plt.show()
207.
208. def draw_pacf(data):
209. # 利用PACF判断模型阶数
210. plot_pacf(data)
211. plt.title("序列偏自相关图(PACF)")
212. plt.show()
213.
214. def draw_acf_pacf(data):
215. f = plt.figure(facecolor='white')
216. # 构建第一个图
217. ax1 = f.add_subplot(211)
218. # 把x轴的刻度间隔设置为1,并存在变量里
219. x_major_locator = MultipleLocator(1)
220. plot_acf(data, ax=ax1)
221. # 构建第二个图
222. ax2 = f.add_subplot(212)
223. plot_pacf(data, ax=ax2)
224. plt.subplots_adjust(hspace=0.5)
225. # 把x轴的主刻度设置为1的倍数
226. ax1.xaxis.set_major_locator(x_major_locator)
227. ax2.xaxis.set_major_locator(x_major_locator)
228. plt.show()
229.
230. draw_acf_pacf(np.array(train_data))
全部代码见:https://download.csdn.net/download/weixin_44026026/87657283