Dijkstra算法+打印路径
原理
Dijkstra 算法(中文名:迪杰斯特拉算法)是由荷兰计算机科学家 Edsger Wybe Dijkstra 提出。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说,如果图中的顶点表示城市,而边上的权重表示城市间开车行经的距离,该算法可以用来找到两个城市之间的最短路径。
设G=(V,E)是一个带权有向图,把图中顶点集合V分为两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),
第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径的的递增次序依次把第二组中的顶点加入S中。在加入的过程中,总保持从源点v到S中各个顶点的最短路径长度不大于从源点v到U中任何路径的长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前路径的最短长度。
一般用于求单源无负权最短路径
算法步骤
1)初始时,只包括源点,即S = {v},v的距离为0。U包含除v以外的其他顶点,即:U ={其余顶点},若v与U中顶点u有边,则(u,v)为正常权值,若u不是v的出边邻接点,则(u,v)权值 ∞;
2)从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
4)重复步骤b和c直到所有顶点都包含在S中。
朴素Dijkstra(邻接矩阵)
测试常量
private static final int N = Integer.MAX_VALUE; // 最大值
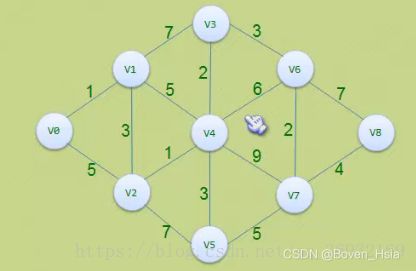
private static char[] vexs = {'0', '1', '2', '3', '4', '5', '6', '7', '8'}; // 顶点集合
private static int[][] matrix = {
{0, 1, 5, N, N, N, N, N, N},
{1, 0, 3, 7, 5, N, N, N, N},
{5, 3, 0, N, 1, 7, N, N, N},
{N, 7, N, 0, 2, N, 3, N, N},
{N, 5, 1, 2, 0, 3, 6, 9, N},
{N, N, 7, N, 3, 0, N, 5, N},
{N, N, N, 3, 6, N, 0, 2, 7},
{N, N, N, N, 9, 5, 2, 0, 4},
{N, N, N, N, N, N, 7, 4, 0}};
朴素Dijkstra算法代码(O(n2)).
参数定义:
prev[j:经过点j
dist[j]:到j点距离
public static void dijkstra(int vs) {
int[] prev = new int[vexs.length];
int[] dist = new int[vexs.length];
boolean[] visit = new boolean[vexs.length];
//初始化
for (int i = 0; i < vexs.length; i++) {
prev[i] = 0;
dist[i] = matrix[vs][i];
}
visit[vs] = true;
dist[vs] = 0;
for (int i = 1; i < vexs.length; i++) {
int min = N, k = 0;
for (int j = 0; j < vexs.length; j++) {
if (!visit[j] && min > dist[j]) {
k = j;
min = dist[j];
}
}
if (min == N) break;
visit[k] = true;
for (int j = 0; j < vexs.length; j++) {
if (matrix[k][j] == N) continue;
if (!visit[j] && dist[j] > min + matrix[k][j]) {
prev[j] = k;
dist[j] = min + matrix[k][j];
}
}
}
// 打印dijkstra最短路径的结果
System.out.printf("dijkstra(%c): \n", vexs[vs]);
for (int i = 0; i < vexs.length; i++)
System.out.printf(" shortest(%c, %c)=%d , p =%d\n", vexs[vs], vexs[i], dist[i], prev[i]);
}
堆优化 Dijkstra(邻接表)
堆优化的主要思想就是使用一个优先队列(就是每次弹出的元素一定是整个队列中最小的元素)来代替最近距离的查找,用邻接表代替邻接矩阵,这样可以大幅度节约时间开销。
这也是一种在图论中十分常见的存图方式,与数组存储单链表的实现一致(头插法)。
这种存图方式又叫「链式前向星存图」。
适用于边数较少的「稀疏图」使用,当边数量接近点的数量,即 时,可定义为「稀疏图」。
int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
int idx;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx;
w[idx] = c;
idx++;
}
首先 idx 是用来对边进行编号的,然后对存图用到的几个数组作简单解释:
he 数组:存储是某个节点所对应的边的集合(链表)的头结点;
e 数组:由于访问某一条边指向的节点;
ne 数组:由于是以链表的形式进行存边,该数组就是用于找到下一条边;
w 数组:用于记录某条边的权重为多少。
因此当我们想要遍历所有由 a 点发出的边时,可以使用如下方式:
for (int i = he[a]; i != -1; i = ne[i]) {
int b = e[i], c = w[i]; // 存在由 a 指向 b 的边,权重为 c
}
void dijkstra() {
// 起始先将所有的点标记为「未更新」和「距离为正无穷」
Arrays.fill(vis, false);
Arrays.fill(dist, INF);
// 只有起点最短距离为 0
dist[k] = 0;
// 使用「优先队列」存储所有可用于更新的点
// 以 (点编号, 到起点的距离) 进行存储,优先弹出「最短距离」较小的点
PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[1]-b[1]);
q.add(new int[]{k, 0});
while (!q.isEmpty()) {
// 每次从「优先队列」中弹出
int[] poll = q.poll();
int id = poll[0], step = poll[1];
// 如果弹出的点被标记「已更新」,则跳过
if (vis[id]) continue;
// 标记该点「已更新」,并使用该点更新其他点的「最短距离」
vis[id] = true;
for (int i = he[id]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[id] + w[i]) {
dist[j] = dist[id] + w[i];
q.add(new int[]{j, dist[j]});
}
}
}
}
}
打印路径
// 打印Dijkstra最短路径的结果
System.out.printf("bellman(%c): \n", vexs[vs]);
for (int i = 0; i < vexs.length; i++) {
System.out.printf(" shortest(%c, %c)=%d , p =%d \t", vexs[vs], vexs[i], dist[i], prev[i]);
StringBuilder sb = new StringBuilder();
sb.append(i);
for (int j = i; j != vs && prev[j] != -1; j = prev[j]) {
sb.append(">--");
sb.append(prev[j]);
}
System.out.println(sb.reverse());
}
缺陷
若u→v间存在一条负权回路(负权回路含义为:如果存在一个环(从某个点出发又回到自己的路径),而且这个环上所有权值之和是负数,那这就是一个负权环,也叫负权回路),那么只要无限次地走这条负权回路,便可以无限制地减少它的最短路径权值,这就变相地说明最短路径不存在。一个不存在最短路径的图,Dijkstra 算法无法检测出这个问题,其最后求解的dist[]也是错的。
对比
Dijkstra: 不含负权。运行时间依赖于优先队列的实现,如 O((∣V∣+∣E∣)log∣V∣)
SPFA: 无限制。运行时间O(k⋅∣E∣) (k≪∣V∣)
Bellman-Ford:无限制。运行时间O(∣V∣⋅∣E∣)
ASP: 无圈。运行时间O(∣V∣+∣E∣)
Floyd-Warshall: 无限制。运行时间O(∣V∣^3)
Dijkstra:适用于权值为非负的图的单源最短路径,用斐波那契堆的复杂度O(E+VlgV)
BellmanFord:适用于权值有负值的图的单源最短路径,并且能够检测负圈,复杂度O(VE)
SPFA:适用于权值有负值,且没有负圈的图的单源最短路径,论文中的复杂度O(kE),k为每个节点进入Queue的次数,且k一般<=2,但此处的复杂度证明是有问题的,其实SPFA的最坏情况应该是O(VE).
Floyd:每对节点之间的最短路径。
这里给出结论:
(1)当权值为非负时,用Dijkstra。
(2)当权值有负值,且没有负圈,则用SPFA,SPFA能检测负圈,但是不能输出负圈。
(3)当权值有负值,而且可能存在负圈,则用BellmanFord,能够检测并输出负圈。
(4)SPFA检测负环:当存在一个点入队大于等于V次,则有负环,后面有证明。