贪心算法思想详解+示例代码

CSDN话题挑战赛第2期
参赛话题：学习笔记

五大算法思想

1. 分治思想
2. 贪心算法/贪婪算法
3. 动态规划
4. 动态回溯
5. 分支定界

贪心算法

今天我们来学习贪心算法。
什么是贪心算法，顾名思义，就是你要贪，做题要学会贪。

实际上，贪心算法就是把大的问题归纳成小问题，然后得到解决的思想，贪心算法是一种思想，没有什么固定的公式与套路。

贪心算法是指在对问题求解时，总是做出在当前看来是最好的选择。
也就是说，不从整体最优上加以考虑，只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

贪心算法解题的一般步骤是：
1.建立数学模型来描述问题；
2.把求解的问题分成若干个子问题；
3.对每一子问题求解，得到子问题的局部最优解；
4.把子问题的局部最优解合成原来问题的一个解。

到目前位置，我们已经了解过贪心算法的思想了，比如A星寻路算法，他就是寻找每个路径的最小代价，进而找到对于当前情况来说的最优解，但他并不一定是全局最优的，但是它一定是局部最优。
对于A星寻路算法，可以看我这篇博客：A星寻路代码详解
还有一个我们了解的例子，就是选择排序法： 它也是使用了贪心算法的思想.

所以，对于贪心算法：

• 能且只能做当前看来最优的选择 如此反复 试图得到最终最优解。
• 每一步都是局部最优。
• 缺点：并非一定能得到整体最优解。

举例说明

因为贪心算法比较抽象，我们将通过几个例子来深入了解这个算法思想
希望通过这几个例子，可以帮助你更加深入的了解贪心算法，这几个例子只是贪心算法这方面的基础题型，以后我会带领大家往深入的方向了解贪心算法及其他四种算法思想。

选择排序

没错，我们常见的选择排序就是运用了贪心算法的思想，怎么个贪心法呢？
假如你想要让数字从递增排序，选择排序就是从数组的零下标开始，依次从后面找到最小的元素的下标与当前位置的元素互换，这个在后面寻找最小元素的过程就是贪心的思想。

贪心策略：寻找最小的元素，（贪心的）认定此最小元素就是当前位置的最小元素。（递增，递减则相反）

void choice_sort(int* arr,int len)
{
	for (int i = 0; i < len - 1; i++)
	{
		int minIdx = i;
		for (int j = i + 1; j < len; j++)
		{
		
			minIdx = (arr[minIdx] < arr[j]) ? minIdx : j;
		}
		auto temp = arr[minIdx];
		arr[minIdx] = arr[i];
		arr[i] = temp;
	}
}

删除数字

我们可以输入任意位数的数字num（不局限于整数类型），我们可以指定删除任意n位数。请问：当我们去除n位后，这个数字序列所能组成的最小数字是多少？注意：数字保持原有序列，不能更改顺序
示例：
输入： num：178453 n：4
结果：13
输入： num：156263 n：4
结果：12

解析：对于数字 178453 删除任意四位数，剩下的数字还有两个，也就是说我们要找到剩下的两个数字的最大的那一种情况，我们只能删除中间四位， 那么我们剩下 1和3 ，也就是13 ，13即是数字删除4位后最小的数字。没有别的情况。对于数字156263也是，只有删除5663后，剩下的数字12是最小的。我们也不能更改数字的顺序。

贪心思想：既然我们要找到删除后最小的数字组成的序列，那我们就找到原序列中最大的数字删掉不就好了？
贪心策略：寻找序列中最大的n位数字，删除（或者覆盖），那么剩下的就是最小的数字序列。

#include 
#include 
using namespace std;
int main()
{
	string num;
	cin >> num;
	int len = num.size();
	
	int n = 0;
	int k;
	cin >> k;	//删除的位数
	while (k--)
	{
		//每次都寻找此序列中最大的数字（寻找局部最优解）
		while (n < len && num[n] <= num[n + 1])
		{
			n++;
		}
		//找到局部最优解后，后面的数字覆盖过来，把他删除
		for (int i = n + 1; i < len; i++)
		{
			num[i - 1] = num[i];
		}
		//数字长度减1
		len--;
		//重置寻找局部最大值
		n = 0;
	}
	for (int i = 0; i < len; i++)
	{
	//我们只是覆盖那些数字了，并没有删除，根据剩下的长度找到最小序列
		cout << num[i];

	}
	return 0;
}

寻找数字最大和

我们有很多条路径，每个路径对应一个数字，我们的终点是 数字9，我们要到走到终点，第五行每个数字都可以当作最后的终点，你要选择一条合适的路径，使得路径上的数字之和相加最大，并且输出这条路径的数字之和。（不能往回走，但是可以用不同的路径走相同的数字，例如，3可以走2次，从4走过来，或者从7走过来）。
结果： 28

我们要找到路径最大的一种方式，这个题的题解有很多，你也可以使用暴力搜索的方式，依次遍历每一条路径，最后比较得到最大数字的路径，但是这样的方式会很慢，我们没有必要遍历每一条路径。
我们可以采取这种方式：从起点出发，当我们遇到分岔路的时候，先别着急走，先计算下一个数字与现在的数字之和，如果右边数字之和大于左边，则走右边，反之走左边。例如， 9 + 4 = 13； 9 + 7 =16 ，那么我们一定选择 7这条路径，我们就不用走左边4这条路径了。

我们不妨从下往上走，从终点直到起点，我们的每一步都按照贪心的思想走，走和最大的路，则我们到达起点时，一定是正确的路径（即和最大）。

贪心思想：依次计算当前数字和下面的数字之和，分别计算当前数字与下面多个数字的和，选择最大数字之和的那一条路径走。
贪心策略：选择当前数字与下面多条路径数字之和最大的那一条路走。

#define NUM 5
int getMaxPath(int i, int j)
{
	/*
	从下往上走
	*/
	int temp[NUM][NUM]{ 0 };
	//先给最后一行赋值
	for (int j = 0; j < NUM; j++)
	{
		temp[NUM - 1][j] = arr[NUM  - 1][j];		//注意，行数有五行，但是下标从0 - 4
	}

	//在从倒数第二行开始依次相加
	for (int i = NUM - 2; i >= 0; i--)
	{
		for (int j = 0; j <= i; j++)
		{
			//当前数字等于当前数字加上下一行的最大的那个数字
			temp[i][j] = arr[i][j] + Max(temp[i+1][j], temp[i+1][j + 1]);	//Max函数即求两数字最大值
		}
	}
	return temp[0][0];	//最顶部一定是最大的
}

买股票

解析：你今天买了股票，下次就要卖出，不能连续两天都买或者卖，只能买卖操作，让你求怎么买或者卖，得到的利润最大。

贪心思想：既然是买股票，那你就计算今天和明天，这两天的股票价之差是否大于零（是否是盈利）就行呗。你管他赚的多还是少，只要赚钱你就买卖呗，如果是负的（亏损），则不买不卖。
贪心策略：只要这两天的股票利润为正，就买入卖出。

int maxProfit(vector<int>& prices) {
   int total=0;
    for (int i=0;i<prices.size()-1;i++)
    {
        int temp=prices[i+1]-prices[i];
        if (temp>0)
        {
            //只要是正利润，那你就买呗
            total+=temp;
        }
    }
    returntotal;
} 

---

最大回文字符串

注意：题目没有说明这些数字的顺序不能改变，因此这题，字符的顺序都是可以改变的，任你随便怎么顺序，只要能构成一个回文字符串，就行，要求你输出能够组成的最大回文串的长度。

解析：我们观察到，回文串的左右两侧是对称的，并且假设有一个回文中心，奇数个数的回文串回文中心是一个单独出现的字母（或者是奇数个数的字母的单独的哪一个），偶数个数的回文串的回文中心是一条你看不见的线（因为偶数回文串左右完全对称）。
因此：回文串可以由两种情况：

1. 全部都是偶数，回文串左右完全对称。
2. 存在某个字母个数为奇数，例如3个a，则把两个a放在左右两端，单独的a放在回文中心。

贪心思想：只要某个单词出现了偶数次，就把回文串长度加2（白给的两个一样的字母，你不放左右两边，你还想放哪？？？）；如果有多余的奇数个字母，则回文串加2，再单独一次加1（当作回文中心），注意：此后如果再出现1个或者已经分离了的奇数个，则长度无法再次加1
贪心策略：单词出现偶数次，长度加2；出现奇数次，判断长度是否能够加2（有一个专门的公式），再单独加1

int longestPalindrome(string s) {
	  map<char,int> count_c;
	  for (auto& x:s)
	  {
	      count_c[x]++;
	  }
	
	  int len=0;
	  for (auto& x:count_c)
	  {
	      int temp=x.second/2*2;
	      len+=temp;
	      if (temp%2 && len%2==0)
	      {
	          len+=1;
	      }
	  }
	  return len;
}

我可能描述的不是很清晰，关于这道题的详细解释，请看leetcode官方解释：
最长回文串

背包问题

背包问题
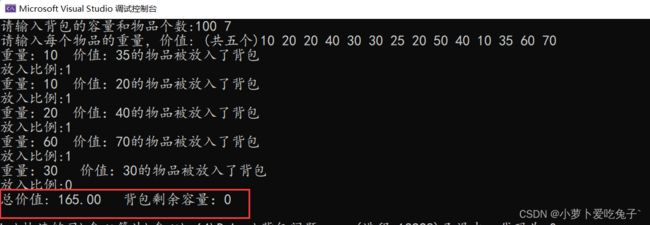
有一个背包，容量由你自己输入，有n个物品，每个物品都具有容量与价值，这些都是由你自己输入的，请问，要怎么放物品到背包里，才能使得总价值最大呢，放入背包的总容量要小于等于背包的总容量。（如果一个物品放不下，则可以拆分成多个小块）
背包：M：100
物品：N：7
重量 价值
10 20
20 40
30 30
25 20
50 40
10 35
60 70

结果：

解析：每个物品都具有其重量与价值，我们不妨计算出每个物品的单位价值。
单位价值指的是：每重量的价值。 然后我们将这些物品按照单位价值递减排序。
这样一来，我们就简单了，只需用贪心，依次把最大单位价值的物品价值和容量相加就行了。

贪心思想：单位价值最大的物品，我们假设他就是最好的，则直接把他放在背包里面。
贪心策略：单位价值最高，直接把它放包里。

#include 
#include 
using namespace std;

const int SIZE = 100;

struct box
{
	int w;	//物品重量
	int p;	//物品价格
	double w_p;	//单位价格（每重量的价值）
};

int cmp(const box& a,const box& b)
{
	return a.w_p > b.w_p;	//递减
}

int main()
{
	int M;	//背包总容量
	int n;
	printf("请输入背包的容量和物品个数:");
	//scanf("%d", &M);
	cin >> M >> n;
	box tools[SIZE];
	printf("请输入每个物品的重量，价值: (共五个)");
	for (int i = 0; i < n; i++)
	{
		//scanf("%d %d", &tools[i].w, &tools[i].p);
		cin >> tools[i].w >> tools[i].p;
		tools[i].w_p = (double) tools[i].p / tools[i].w;
	}
		
	/*
	对单位价值按照从大到小的顺序排序
	*/
	sort(tools, tools + n, cmp);

	/*
	贪心思想： 每次只把单位价值最高的相加，寻找局部最优解
	*/
	double total_p = 0;		//总利润
	for (int i = 0; i < n; i++)
	{
		//背包容量大于此物品的容量
		if (M >= tools[i].w)
		{
			//总价值相加
			total_p += tools[i].p;
			//背包容量减去这个物品
			M -= tools[i].w;
			cout << "重量：" << tools[i].w << "  价值：" << tools[i].p << "的物品被放入了背包" << endl << "放入比例:" << 1 << endl;
		}
		else
		{
			//背包容量已经不能放下一整个物品了，只能放一部分，只把这一块的价值相加
			total_p += (M * tools[i].w_p);
			cout << "重量：" << tools[i].w << "   价值：" << tools[i].p << "的物品被放入了背包" << endl << "放入比例:" << M / tools[i].w<< endl;

			break;	//结束了
		}
	}
	printf("总价值: %.2lf\t 背包剩余容量：%d\n", total_p, M);
	return 0;
}

小结

我们学习了贪心算法的基本思想，贪心算法比较抽象，它就是在局部找到最优的情况，还有一种思想，动态规划，他是在全局找到最优解的情况，我们下节再说。

另外，如果在文章中找到了错误，欢迎指正，我也是初学者，我们共同进步！