计算机组成原理（二）—— 数据的表示与运算
系列文章目录
第一章 计算机系统概述
第二章 数据的表示与运算
第三章 存储系统
第四章 指令系统
第五章 中央处理器
第六章 总线
第七章 输入/输出系统
第二章 数据的表示与运算
系列文章目录
引言
一、数制与编码
1.1 进位计数制
1.1.1 进制及转换
1.1.2 真值、机器数
1.2 BCD码
1.3 ASCII 码
1.4 校验码
1.4.1 奇偶校验码
1.4.2 海明码
1.4.3 CRC循环冗余码
二、定点数的表示和运算
2.1 定点数的表示
2.1.1 无符号
2.1.2 有符号（原码、反码、补码、移码）
2.2 定点数的运算
2.2.1 移位运算
2.2.2 加减运算（溢出判断）
2.2.3 乘法运算
2.2.4 除法运算
2.3 强制类型转换
2.4 数据的存储和排列
三、浮点数的表示和运算
3.1 浮点数的表示
3.1.1 浮点数的作用和基本原理
3.1.2 浮点数规格化
3.2 浮点数标准 IEEE 754
3.3 浮点数的运算
3.3.1 加减运算
3.3.2 强制类型转换
四、算术逻辑单元ALU
4.1 电路基本原理
4.2 加法器设计
引言
本篇文章我们要探讨的内容有如下两点：
- 数据如何在计算机中表示？
- CPU中的运算器如何实现数据的算数和逻辑运算？其中包括对定点数和浮点数的讨论
一、数制与编码
1.1 进位计数制
1.1.1 进制及转换
所谓进位计数法是一种计数方法，咱们最常用的莫过于十进制了，除此之外还有八进制、十六进制等。这里不得不提几个概念术语：
- 基数：比如说十进制、八进制和十六进制，它们的基数分别为10（0~9）、8（0~7）、16（0~15）
- 数位：比如二进制数1010，这里就有4个数位，从高位到低位依次的数码值为1、0、1、0
- 数码：比如八进制，那么数码，即数码值的范围为（0~7）
- 位权：每个数码所表示的数值等于该数码值乘以一个与它所在位有关的常数，这个常数称为位权。
- 基数和数码的关系：每个数位所用到的不同数码的个数称为基数
1.1.2 真值、机器数
- 真值：我们日常见到的，有
“+”、“-”号的数为真值，比如：+15，-8。真值是机器数所代表的实际值，一般为十进制数。 - 机器数：将
“符号->数字化”的数。一般为二进制数，比如带符号位的 4 位二进制数 0110，最高位0就是符号位，这个数的真值就是 +6。通常0代表“+”号，1代表-号。
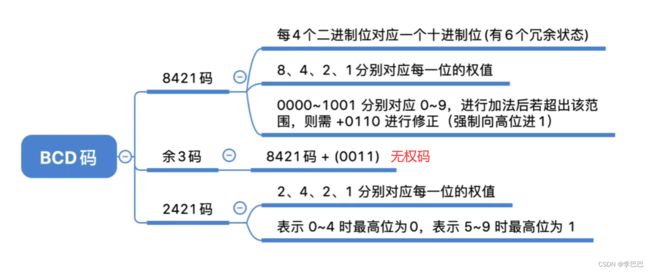
1.2 BCD码
BCD 码就是用 4 个 bit 位（二进制数）对应 1 个十进制位，是一种二进制的数字编码形式，用二进制编码来代替十进制代码。
- 8421 码的运算
- 余 3 码（无权码）
- 2421 码
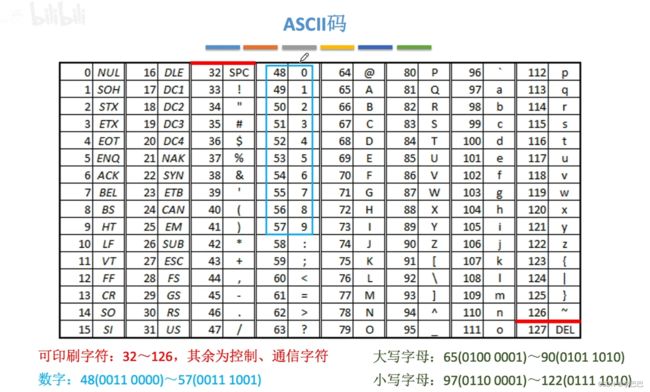
1.3 ASCII 码
我们知道我们日常见到的数字（0~9）、符号比如：#、%、+、@等、英语字母如：(A~z)、(a~z),它们在计算机中都是以二进制来表示存储的，咱们可以用不同的二进制数来表示，但是为了统一化、使大家的相互通信可以正常进行，那么就必须制定一套统一的标准来规范它，由此ASCII码随之诞生，大家都遵从这一统一的标准进行数据的通信和交流。至于ASCII码代表的意思，可参考百科。
小结（梳理一下本小节的知识点叭！！！）：
1.4 校验码
1.4.1 奇偶校验码
奇偶校验码的码距 d = 2 ，仅能检测出奇数位错误，无纠错能力。
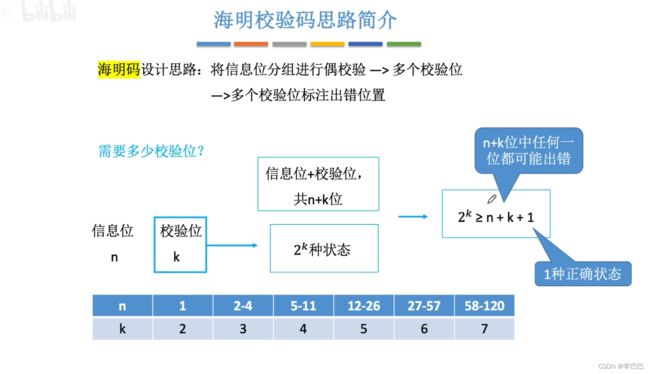
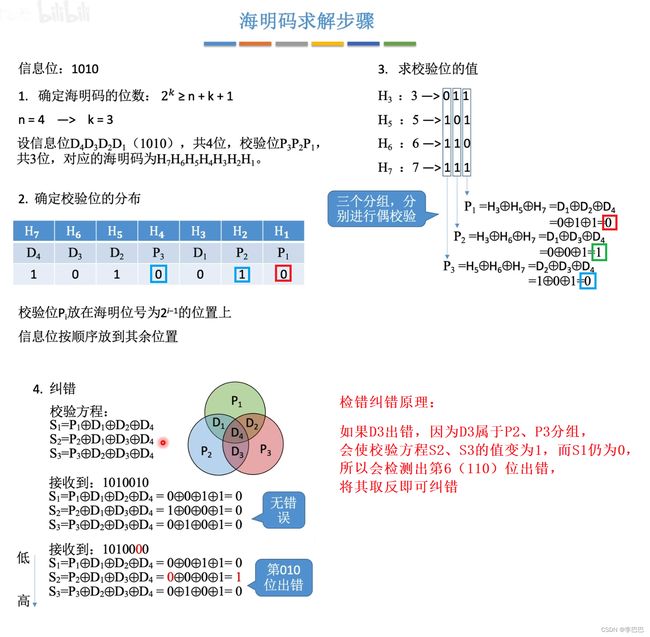
1.4.2 海明码
海明码有 2 位检错能力和 1 位纠错能力，即当有一个 bit 位发生错误时可以纠错，两个 bit 位发生错误只能检测出错误，无法进行纠错。
当有 bit 位发生错误时，为了区分错误位有 1 位还是 2 位，需要添加 “全校验位” 对整体进行偶校验。判断规则如下：
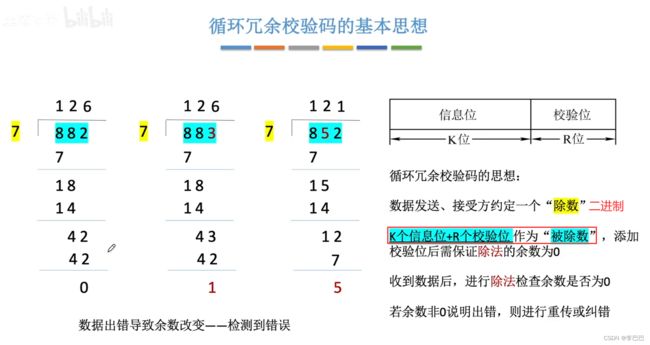
1.4.3 CRC循环冗余码
注意：通过检错得到的余数为 010 就证明是 C2 出错的说法是不严谨的，其并不是严格的二进制 -> 十进制的转换，下面通过还是通过上面的例子来说明：
下面再来看一种信息位较短的例子：
理论上，循环冗余校验码的检错能力有以下特点：
- 可检测出所有奇数个错误
- 可检测出所有双比特的错误
- 可检测所有小于等于检验位长度的连续错误
CRC 循环冗余码实际应用中一般只用来“检错”，不用来“纠错”。
二、定点数的表示和运算
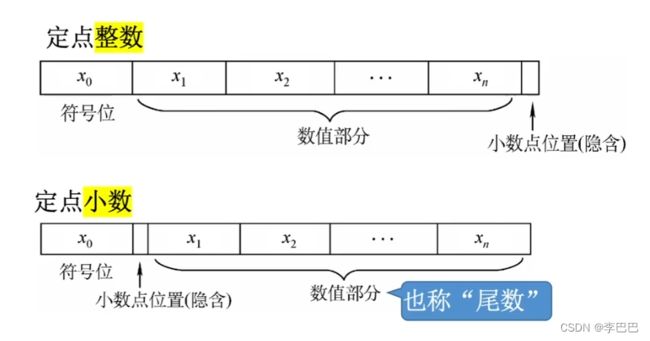
2.1 定点数的表示
2.1.1 无符号
整个机器字长的全部二进制位均为数值位，没有符号位，相当于数的绝对值。若机器字长为 8 位，则数的表示范围 0~255。（通常只有无符号整数，没有无符号小数）
2.1.2 有符号（原码、反码、补码、移码）
在机器中，数的正负我们无法识别，但是我们可以用二进制数来代替正负号。一般‘0’为正，‘1’为负，符号位一般在有效数的最前面。
有符号数的定点表示
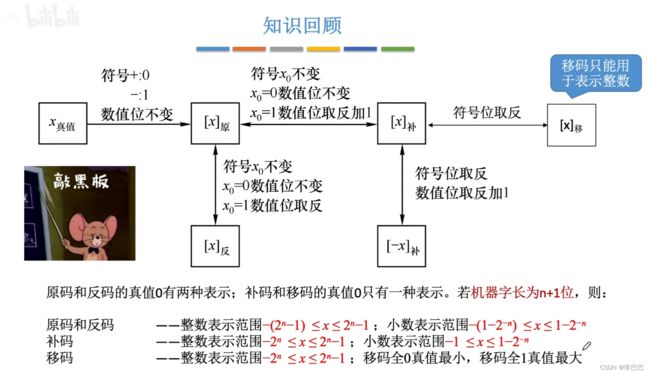
注：可用 原码、反码、补码 三种方式来表示定点整数和定点小数，还可用 移码 表示定点整数。
① 原码：用尾数表示真值的绝对值，符号位 “0/1” 对应 “正/负”。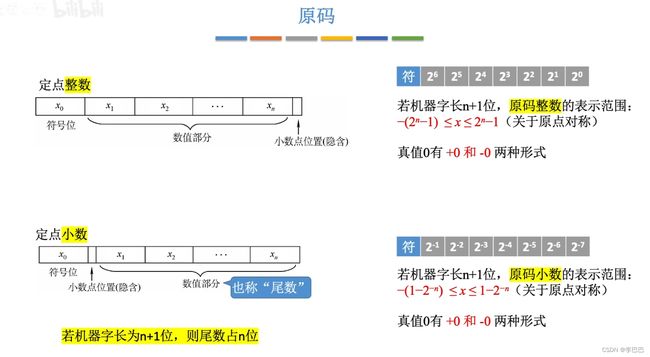
② 反码：若符号位为 0，则反码原码都相同。若符号位为 1，则数值位全部取反。（反码的取值范围与原码相同）
③ 补码：正数的补码 = 原码； 负数的补码 = 反码末位 + 1（要考虑进位）
补码的作用：让减法操作转变为与之等价的加法操作，节省硬件成本。
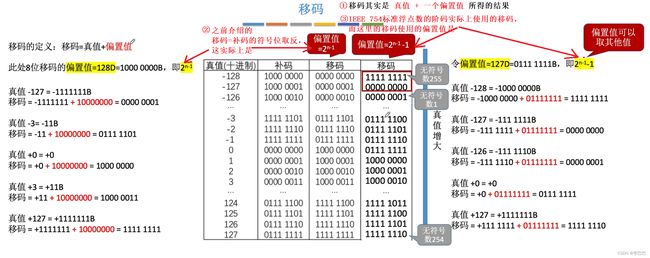
④ 移码：在补码的基础上，将符号位取反。移码只能用于表示整数。（移码的取值范围与补码相同）
移码有什么作用呢？在进行数值比较时，用移码表示的整数符合计算机比较的特性（从前往后先出现1的大），很容易对比大小
小结（梳理一下本小节的知识点叭！！！）： 
2.2 定点数的运算
2.2.1 移位运算
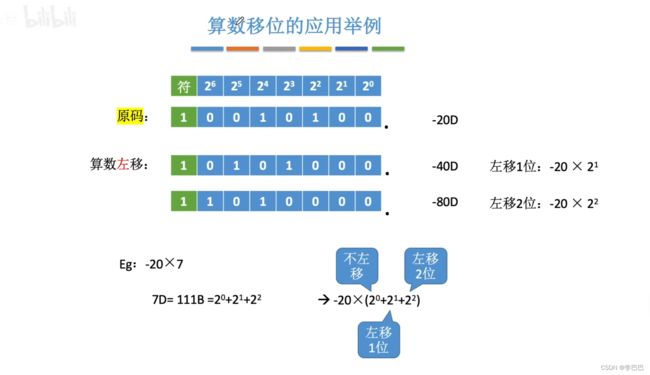
移位：通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。可用移位运算实现乘法、除法。
算数移位：
① 原码的算术移位：符号位保持不变，仅对数值位进行移位。
- 右移：高位补0，低位舍弃。若舍弃的位 = 0，则相当于 ÷ 2 ；若舍弃的位 ≠ 0，则会丢失精度
- 左移：低位补0，高位舍弃。若舍弃的位 = 0，则相当于 × 2 ；若舍弃的位 ≠ 0，则会出现严重错误
② 反码的算术移位：
③ 补码的算术移位：
注意：由于位数有限，因此有时候无法用算术移位精确地等效乘除法
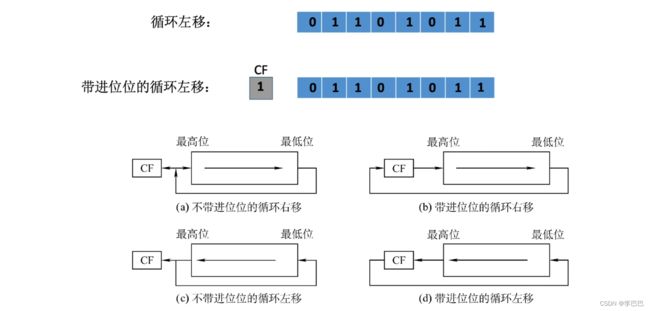
逻辑移位：
- 逻辑右移：高位补 0，低位舍弃
- 逻辑左移：低位补 0，高位舍弃
逻辑以为可以看作对 “无符号数” 的算术移位。
循环移位：
注意：以下的加、减、乘、除运算都是分别对 原码 和 补码 的讨论
2.2.2 加减运算（溢出判断）
① 原码的加减运算
② 补码的加减运算
对于补码来说，无论加法还是减法，最后都会转变成加法，由加法器实现运算，符号位也参与运算。
溢出判断
方法①：采用一位符号位
方法②：采用一位符号位，根据数据位进位情况判断溢出
方法③：采用双符号位
2.2.3 乘法运算
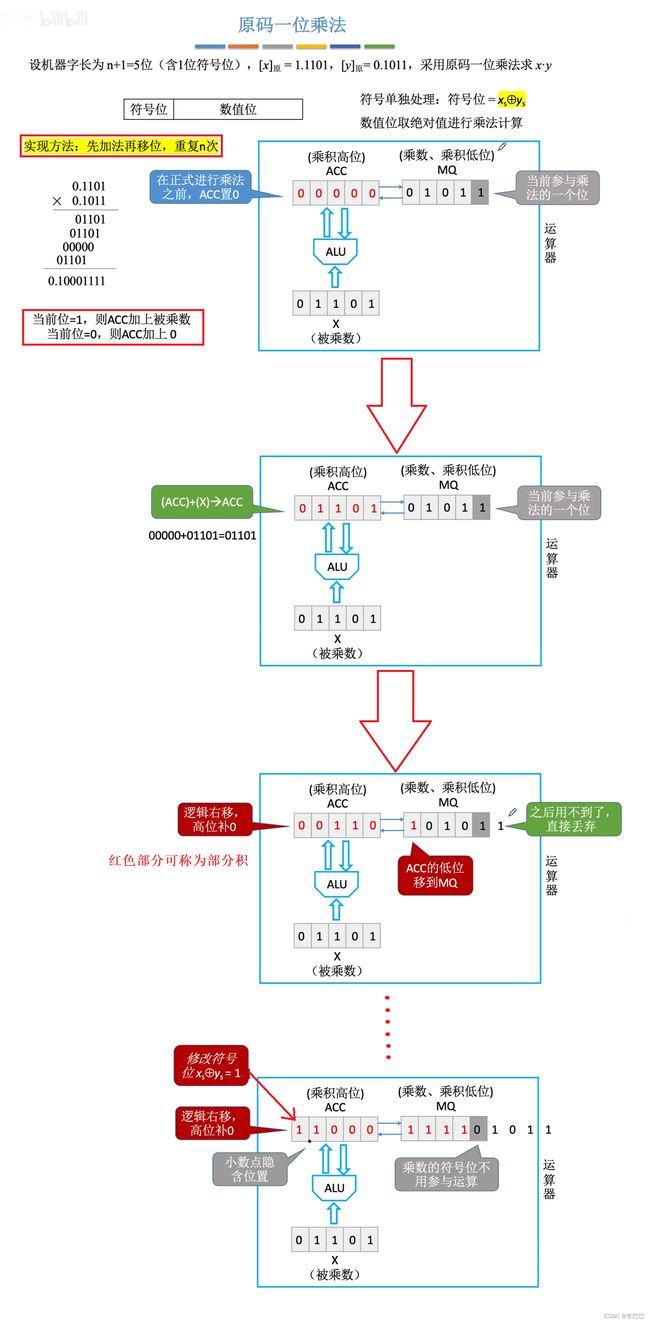
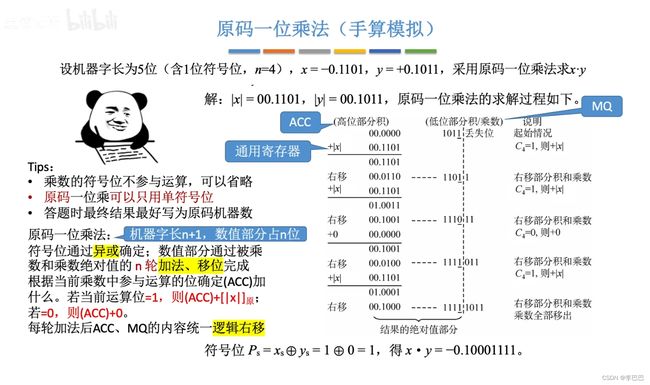
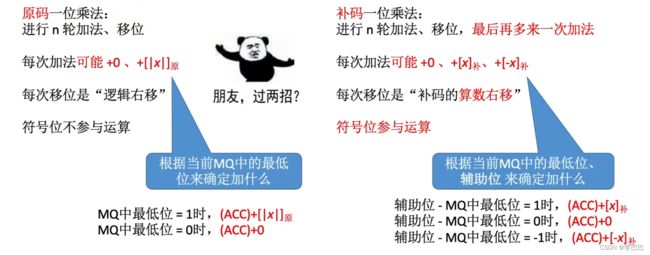
① 原码的乘法运算
② 补码的乘法运算
原码乘法 与 补码乘法 的对比：
2.2.4 除法运算
① 原码的除法运算（恢复余数法）
能否不用在商 1 得到负数后进行恢复余数的操作？答案当然是可以的！
我们成改进后的方法为：加减交替法
② 补码的除法运算
原码除法 与 补码除法 的对比：
2.3 强制类型转换
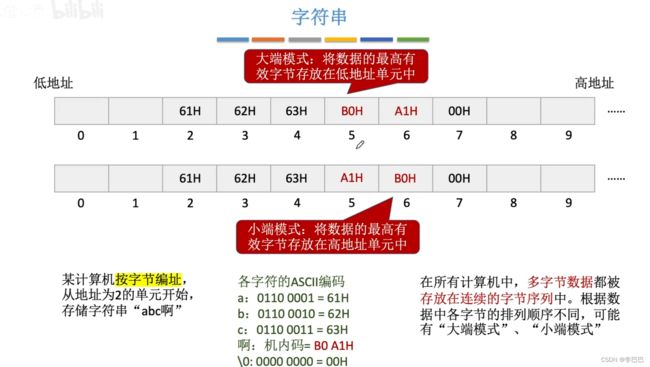
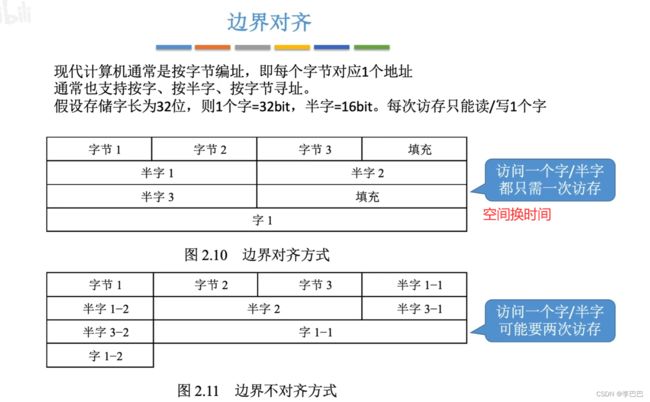
2.4 数据的存储和排列
三、浮点数的表示和运算
3.1 浮点数的表示
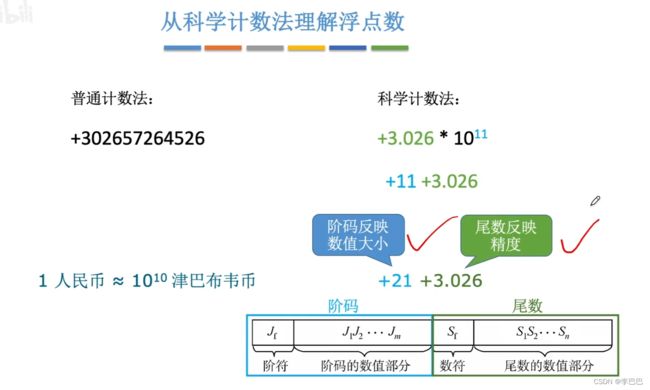
3.1.1 浮点数的作用和基本原理
定点数可表示的数字范围有限，从 short(2字节) 类型到 int(4字节) 类型再到 long(8字节) 类型，但我们不能无限制地增加数据的长度，那我们该如何在位数不变的情况下增加数据表示范围呢？解决办法就是接下来要介绍的浮点数
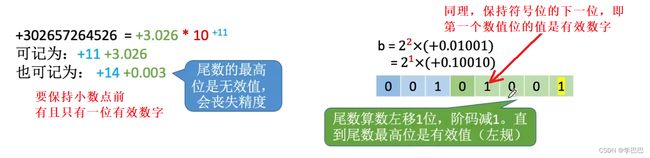
3.1.2 浮点数规格化
如何解决上图例题中的精度损失问题呢？这里就要用到浮点数尾数的规格化
小结（梳理一下本小节的知识点叭！！！）： 
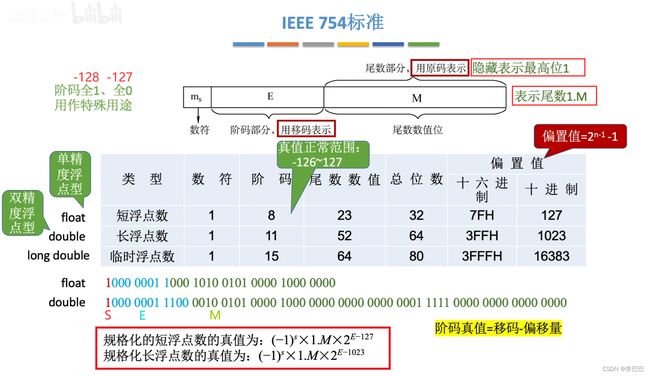
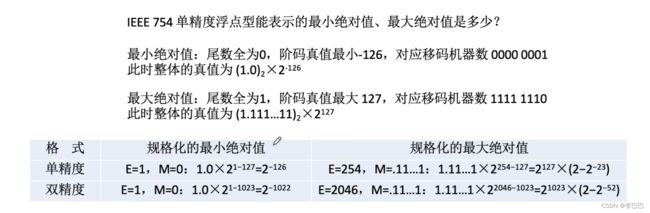
3.2 浮点数标准 IEEE 754
浮点数的阶码、尾数到底使用什么码？各取多少位比较合适？本小节我们就来讨论这个问题。
在介绍本小节内容前，我们先来回顾一下移码：
下面我们来看两个例题：
3.3 浮点数的运算
3.3.1 加减运算
3.3.2 强制类型转换
小结（梳理一下本小节的知识点叭！！！）： 
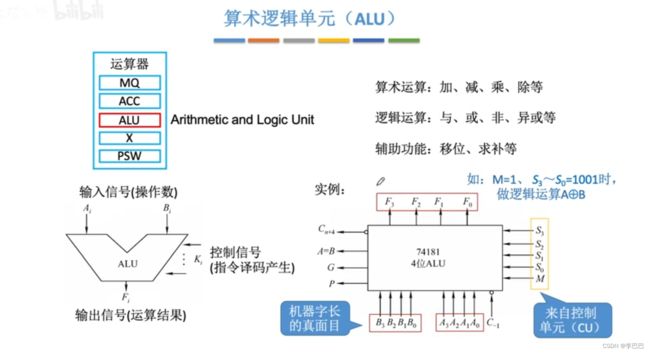
四、算术逻辑单元ALU
4.1 电路基本原理
4.2 加法器设计
加法器优化过程：
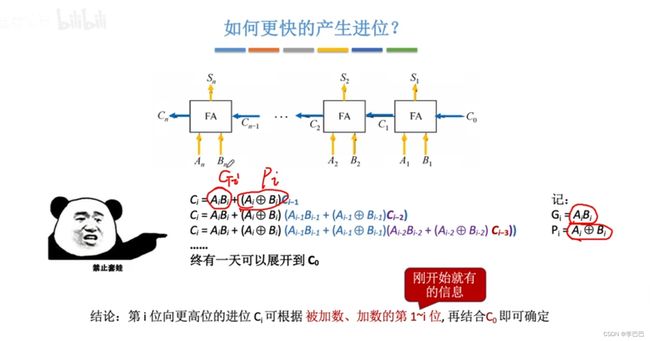
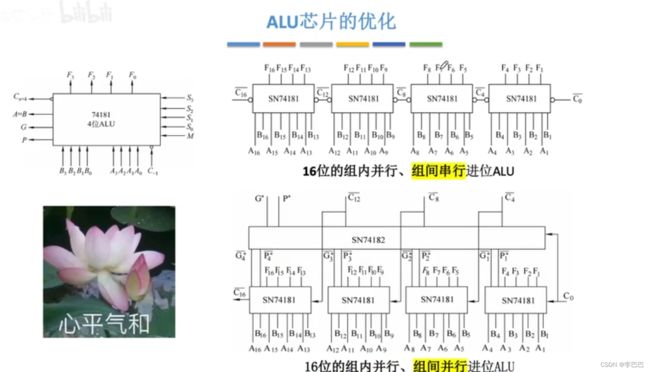
串行加法器 ----> 串行进位的并行加法器 ----> 组内并行、组间串行进位的加法器 ----> 组内并行、组间并行进位的加法器