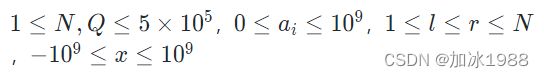差分与前缀和

差分与前缀和是一对互逆的操作，该算法常用于求解区间问题，差分主要用于多次对区间进行加减操作的问题，而前缀和主要用于多次对区间进行求和的问题。

差分

当对某些不确定的区间多次进行加减操作时，如果每次都是对这些区间遍历操作，那么时间复杂度是O(nm)。而如果我们采用差分法来求解，就是先构造一个差分数组，然后转化为对区间端点的操作，这样的话时间复杂度就转化为O(n)。

但是需要注意的是，差分法只能用于多次对区间进行加减的运算，不能用于乘除运算。

差分算法解题步骤：

1、构造差分数组：b[1]=a[1]，从第二项开始：b[i]=a[i]-a[i-1];

2、对区间端点进行加减：b[l]+=x；b[r+1]-=x;

3、差分还原（前缀和）；

4、差分数组一般都是从1开始，这样比较方便，b[1]=a[1]-a[0]=a[1]-0;

举例说明：

现有数组:a[]=[1 2 3 4 5 6 8];

差分后的数组为：b[]=[1 1 1 1 1 1 2];

现需要对该数组中的某些区间l,r进行加减操作：

1、对第2到第5个数进行+3操作；

2、对第3到第6个数进行-1操作；

……

对于第一个：

b[2]+=3;

b[5+1]-=3;

则：b[]=[1 4 1 1 1 -2 2]；

差分还原：

原数组：a[]=[1 2 3 4 5 6 8];

现在数组：a[]=[1 5 6 7 8 6 8]；

我们发现确实是对第2到第5个数进行了+3操作；

对于第二个(这一次的修改是在第一次修改的基础上)：

b[3]+=(-1);

b[6+1]-=(-1);

则：b[]=[1 4 0 1 1 -2 3 ];

差分还原：

原数组：a[]=[1 5 6 7 8 6 8]；(这一次的原数组应该是第一次操作后的数组）

现在数组：a[]=[1 5 5 6 7 5 8];

我们发现也确实是与预想一样；

当然我们实际解题的时候并不需要把每一次的步骤还原，而只需要在最后依次做完时再差分还原；

例题：小明的彩灯

题目描述

小明拥有 N 个彩灯，第 i 个彩灯的初始亮度为 a_i​。

小明将进行 Q 次操作，每次操作可选择一段区间，并使区间内彩灯的亮度 +x（x 可能为负数）。

求 Q 次操作后每个彩灯的亮度（若彩灯亮度为负数则输出 0）。

输入描述

第一行包含两个正整数 N，Q分别表示彩灯的数量和操作的次数。

第二行包含 N 个整数，表示彩灯的初始亮度。

接下来 Q行每行包含一个操作，格式如下：

l r x，表示将区间 l∼r 的彩灯的亮度 +x。

输出描述

输出共 1 行，包含 N 个整数，表示每个彩灯的亮度。

输入输出样例

示例 1

输入

5 3
2 2 2 1 5
1 3 3
4 5 5
1 1 -100

输出

0 5 5 6 10

运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

代码：

#include 
using namespace std;
int a[100010];
long long int b[100010];
int main()
{
  int n,q;
  cin>>n>>q;
  for(int i=1;i<=n;i++)
  {
    cin>>a[i];
    b[i]=a[i]-a[i-1];
  }
  for(int i=1;i<=q;i++)
  {
    int l,r,x;
    cin>>l>>r>>x;
    b[l]+=x;
    b[r+1]-=x;
  }
  for(int i=1;i<=n;i++)
  {
    b[i]=b[i]+b[i-1];
  }
  for(int i=1;i<=n;i++)
  {
  	if(b[i]<0)
  	b[i]=0;
  	cout<

前缀和 

前缀和就是我们所说的前n项数列求和，如果采用普通的方法，时间复杂度也将达到O(nm)；

但是我们采用前缀和时就是构造一个前缀和数组，然后转化为对端点的操作。

前缀和求解基本思路 

1、构造前缀和数组：sum[i]=sum[i-1]+a[i]（注意不管是差分还是前缀和，我们一般都是从1开始，第0项默认为0；

2、 对端点进行求和：sum[l,r]=sum[r]-sum[l-1];

3、前缀和数组会多一个，就是第0个，默认都是0； 

举例说明

这里我们就举一个例子，搞懂原理就行；

现有数组a[]=[1 2 3 4 5 6 8];

1、对第2到第5个数进行求和

……

 前缀和数组：sum[]=[0 1 3 6 10 15 21 29]

 sum[2,5]=sum[5]-sum[2-1]=15-1=14;

我们发现2+3+4+5=14，与所求相等；

例题：大学里的树木要维护

题目描述

教室外有 N棵树（树的编号从 1∼N），根据不同的位置和树种，学校已经对其进行了多年的维护。

因为树的排列成线性，且非常长，我们可以将它们看作一条直线给他们编号。

由于已经维护了多年，每一个树都由学校的园艺人员进行了维护费用的统计。

每棵树的前期维护费用各不相同，但是由于未来需要要打药，所以有些树木的维护费用太高的话，就要重新种植。

由于维护费用也称区间分布，所以常常需要统一个区间里的树木的维护开销。

现给定一个长度为 N的数组 A以及 M个查询，Ai​ 表示第 ii 棵树到维护费用。对于每个查询包含一个区间，园艺人员想知道该区间内的树木维护的开销是多少。

请你编写程序帮帮他！

输入描述

每组输入的第一行有两个整数 N和 M。N 代表马路的共计多少棵树，M代表区间的数目，N和 M 之间用一个空格隔开。

接下来的一行，包含 N 个数 A1​,A2​,⋯,AN​，分别表示每棵树的维护费用，每个数之间用空格隔开。

接下来的 M 行每行包含两个不同的整数，用一个空格隔开，表示一个区域的起始点 L和终止点 R 的坐标。

输出描述

输出包括 M行，每一行只包含一个整数，表示维护的开销。

输入输出样例

示例

输入

10 3
7 5 6 4 2 5 0 8 5 3
1 5
2 6
3 7

输出

24
22
17

运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

代码：

#include 
using namespace std;
int a[1010],sum[1010];
int main()
{
  int n,m;
  cin>>n>>m;
  for(int i=1;i<=n;i++)
  {
    cin>>a[i];
    sum[i]=sum[i-1]+a[i];
  }
  int ans=0;
  for(int i=1;i<=m;i++)
  {
    int l,r;
    cin>>l>>r;
    ans+=sum[r]-sum[l-1];
    cout<