基础算法：二维前缀和

二维前缀和C++模板：

S[i, j] = 第i行j列格子左上部分所有元素的和
S[i, j] = S[i-1,j] + s[i,j-1] - S[i-1,j-1] + a[i,j](表示当前的数)
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1-1,y2] - S[x2,y1-1] + S[x1-1,y1-1]

二维前缀和理解：
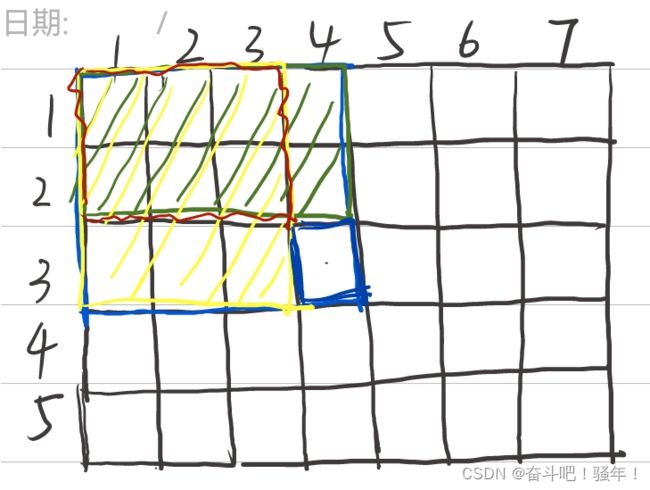
第一步：如何计算S[i, j]？
如下图可以知道，我们要求蓝色的S[3, 4]，那么可以知道可以等于绿色S[2, 4]、黄色S[3, 3]和蓝色a[3 ,4]相加，但是红色S[2 ,3]多加了所以需要减掉。
最后的出公式：S[i, j] = S[i-1,j] + s[i,j-1] - S[i-1,j-1] + a[i,j](表示当前的数)

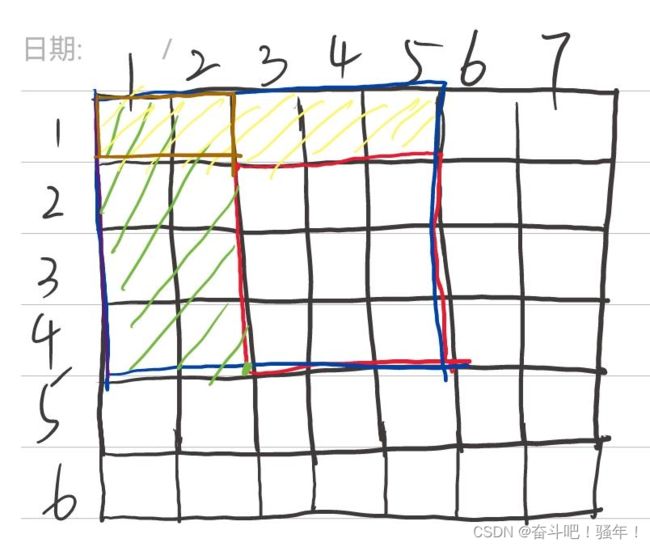
第二步：如何计算以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和？
如下图可以知道，我们要求红色的以(2, 3)左上角和(4, 5)右下角的子矩阵，那么可以知道，为蓝色S[4, 5] -绿色S[4 ,2] - 黄色S[1, 5] + 棕色S[1, 2]
最后得出公式：S[x2, y2] - S[x1-1,y2] - S[x2,y1-1] + S[x1-1,y1-1]

题目： 796. 子矩阵的和
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

#include 
using namespace std;

const int N=1005;
int s[N][N];
int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>s[i][j];
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
        }
    }
    while(q--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;
    }
    return 0;
}