LeetCode_101

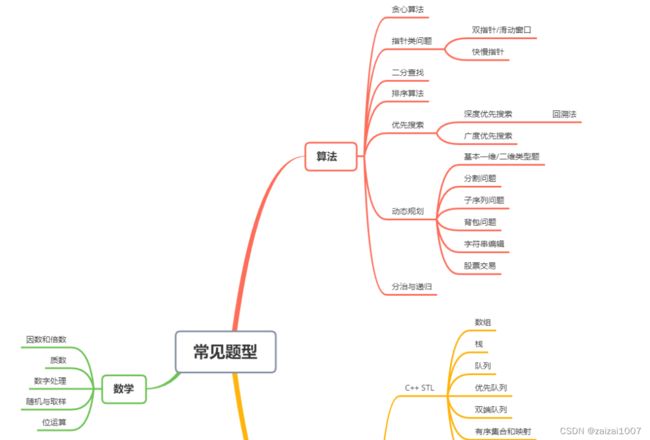
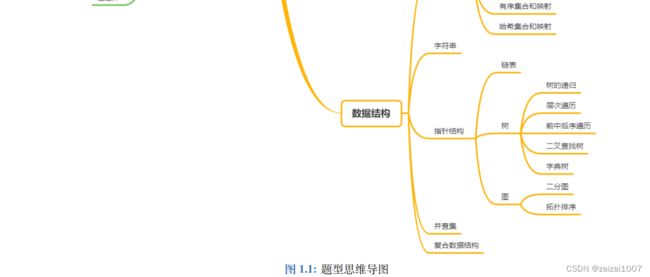
内容提要

 贪心算法

保证每次操作都属局部最优的，从而使得最后的结果是全局最优

全局结果是局部结果的简单求和，且局部结果互不相干

分配问题

分发饼干  455  简单

分发糖果  135  困难

先从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的 糖果数加 1；再从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数 不大于右边孩子的糖果数，则左边孩子的糖果数更新为右边孩子的糖果数加 1

 区间问题

Non-overlapping Intervals  435 中等

 求最少的移除区间个数，等价于尽量多保留不重叠的区间。在选择要保留区间时，区间的结 尾十分重要：选择的区间结尾越小，余留给其它区间的空间就越大，就越能保留更多的区间。因 此，我们采取的贪心策略为，优先保留结尾小且不相交的区间。

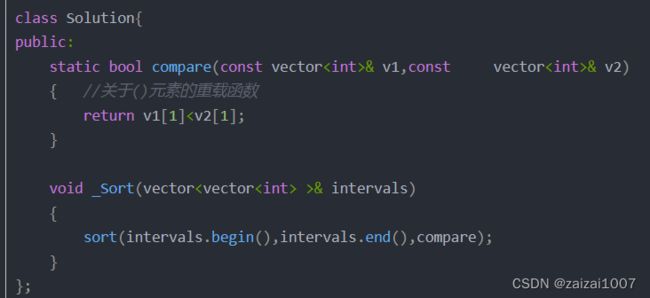
按区间的结尾排序 写法

 解释：

关于vector＜int＞和vector＜vector＜int＞＞的sort函数中的compare函数自定义写法_vector> sort_Shallow_Carl的博客-CSDN博客

更一般的写法：

记得加上前面的stastic 

can place flowers 605 简单

452  minimum number of arrows to burst balloon 中等

763 partition labels 中等

 进阶难度

406  queue reconstruction by height 中等

class Solution {
public:
    vector> reconstructQueue(vector>& people) {
      sort(people.begin(),people.end(),[](const vector& u,const vector& v){
        return u[0] > v[0] || (u[0] == v[0] && u[1] < v[1]);
      });
      vector> ans;
      for(const vector& person: people) {
        ans.insert(ans.begin()+person[1],person);
      }
      return ans;
    }
};

665  non-decreasing array 中等

class Solution {
public:
    bool checkPossibility(vector &nums) {
        int n = nums.size(), cnt = 0;
        for (int i = 0; i < n - 1; ++i) {
            int x = nums[i], y = nums[i + 1];
            if (x > y) {
                cnt++;
                if (cnt > 1) {
                    return false;
                }
                if (i > 0 && y < nums[i - 1]) {
                    nums[i + 1] = x;
                }
            }
        }
        return true;
    }
};

双指针

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务

若两个指针指向同一个数组，遍历方向相同且不会相交，则称为滑动窗口（两个指针包围的区域即为当前的窗口），经常用于区间搜索

若两个指针指向同一个数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是排序好的

指针与常量

int x;

int * p1 = &x; // 指针可以被修改，值也可以被修改

const int * p2 = &x; // 指针可以被修改，值不可以被修改

（const int） int * const p3 = &x; // 指针不可以被修改（* const），值可以被修改

const int * const p4 = &x; // 指针不可以被修改，值也不可以被修改

 指针函数与函数指针

 // addition是指针函数，一个返回类型是指针的函数

int* addition(int a, int b) {

int* sum = new int(a + b);

return sum;

}

int subtraction(int a, int b) {

return a - b;

}

int operation(int x, int y, int (*func)(int, int)) {

return (*func)(x,y);

}

// minus是函数指针，指向函数的指针

int (*minus)(int, int) = subtraction

int* m = addition(1, 2);

int n = operation(3, *m, minus);

 Two Sum

167 Two Sum II - Input array is sorted 中等

因为数组已经排好序，我们可以采用方向相反的双指针来寻找这两个数字，一个初始指向最 小的元素，即数组最左边，向右遍历；一个初始指向最大的元素，即数组最右边，向左遍历。 如果两个指针指向元素的和等于给定值，那么它们就是我们要的结果。如果两个指针指向元 素的和小于给定值，我们把左边的指针右移一位，使得当前的和增加一点。如果两个指针指向元 素的和大于给定值，我们把右边的指针左移一位，使得当前的和减少一点。 可以证明，对于排好序且有解的数组，双指针一定能遍历到最优解。证明方法如下：假设最 优解的两个数的位置分别是 l 和 r。我们假设在左指针在 l 左边的时候，右指针已经移动到了 r； 此时两个指针指向值的和小于给定值，因此左指针会一直右移直到到达 l。同理，如果我们假设 在右指针在 r 右边的时候，左指针已经移动到了 l；此时两个指针指向值的和大于给定值，因此 右指针会一直左移直到到达 r。所以双指针在任何时候都不可能处于 (l,r) 之间，又因为不满足条 件时指针必须移动一个，所以最终一定会收敛在 l 和 r。

归并两个有序数组

 注意 这里我们使用了 ++ 和--的小技巧：a++ 和 ++a 都是将 a 加 1，但是 a++ 返回值为 a，而 ++a 返回值为 a+1。如果只是希望增加 a 的值，而不需要返回值，则推荐使用 ++a，其运行速度 会略快一些。

 快慢指针

 对于链表找环路的问题，有一个通用的解法——快慢指针（Floyd 判圈法）。给定两个指针， 分别命名为 slow 和 fast，起始位置在链表的开头。每次 fast 前进两步，slow 前进一步。如果 fast 可以走到尽头，那么说明没有环路；如果 fast 可以无限走下去，那么说明一定有环路，且一定存 在一个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并 让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点

 滑动窗口

 

 substr()是C++语言函数，主要功能是复制子字符串，要求从指定位置开始，并具有指定的长度。如果没有指定长度_Count或_Count+_Off超出了源字符串的长度，则子字符串将延续到源字符串的结尾。

语法
substr(size_type _Off = 0,size_type _Count = npos)
一种构造string的方法
形式 ： s.substr(pos, len)
返回值： string，包含s中从pos开始的len个字符的拷贝（pos的默认值是0，len的默认值是s.size() - pos，即不加参数会默认拷贝整个s）
异常 ：若pos的值超过了string的大小，则substr函数会抛出一个out_of_range异常；若pos+n的值超过了string的大小，则substr会调整n的值，只拷贝到string的末尾
 

练习

 二分查找

二分查找也常被称为二分法或者折半查找，每次查找时通过将待查找区间分成两部分并只取 一部分继续查找，将查找的复杂度大大减少。对于一个长度为 O(n) 的数组，二分查找的时间复 杂度为 O(log n)。

注意 mid = (l + r)/2 可能会因为 l + r 溢出而错误，因而采用 mid = l + (r − l)/2 的写法。

 

 查找区间

 旋转数组查找数字

 练习