排序模型（learning to rank）发展史（偏推荐系统

前言

「排序」是一个非常业务化的任务，其实践场景也多为搜索、广告、推荐，被用于解决排序任务的模型也被人一统称作了「排序模型」，但其实「排序模型」也是「普通模型」，只不过或多或少在业务层面针对排序做了一些针对。

观察每一类算法模型的发展，最重要的不是事无巨细的记住所有迭代模型的细节，而是明白每一次发生迭代，每一次技术革新，都或多或少解决了上一代模型存在的某一些问题。记住他们迭代的契机，才是通晓了整个历史。

这次就来梳理一下排序模型的发展史。

前深度学习纪元——机器学习与想象力

典中典——协同过滤

提起推荐系统中的算法，最经典的莫过于协同过滤。协同顾虑最早可以追溯到 1992 年，Xerox 的研究中心开发了一种基于协同过滤的邮件筛选系统，用于过滤一些用户不感兴趣的邮件，但在当时并没有引起很大的凡响。

直至 2003 年，Amazon 发表论文《Amazon.com recommendations: item-to-item collaborative filtering》，协同过滤才较为广泛地被人们所知。协同过滤的原理非常简单，就是协同大家的反馈、评价和意见一起对海量信息进行过滤。简单来说，就是「臭味相投」、「一丘之貉」。

	钢铁侠	肖申克的救赎	奇异博士	遗愿清单
用户1	9	6	9	3
用户2	5	10	6	9
用户3	6	9	7	？？？

上表为「共现矩阵」，协同过滤的思路为根据相同爱好的用户，推荐相同的电影，这听上去非常 make sense。在不知道问好处的评分时候，通过已存在的评分，我们发现用户 3 与用户 2 更相似，用户 2 对《遗愿清单》给出了高分，所以用户 3 也应该受到推荐。

每个用户可以用自己的历史行为序列——评分来代表，所以每个用户就是一个向量，所有描述向量相似度的方法都可以用来计算「用户的相似度」，缺失的部分可以用默认值或者均值来代替。在实际场景中用户数量肯定不止例子中的三个，最终结果排序的方式为获取 topn 的相似用户之后，利用他们对目标电影的评分的均值来决定当前用户的评分，也可以利用相似度加权平均。

从另外一个角度，还有「推荐喜欢物品的相似物品」这个思路，其实原理是相似的，也需要共现矩阵，无非列向量代表物品/电影罢了。两类主要是在应用场景上有区别，基于用户的协同过滤使用在偏社交属性的场景，并能够通过相似兴趣的朋友拓展新的兴趣，比如新闻热点。基于物品的协同过滤则适用于兴趣变化比较稳定的场景，比如电商。

协同过滤是一个非常直观、可解释性强的模型，但他有一个很严重的问题——热门物品由于其头部效应，容易跟其他大量物品产生相似性，也就是不管喜欢啥的用户，可能都喜欢头部物品。尾部物品由于向量稀疏，很少与其他物品产生相似性，导致很少被推荐。推荐结果头部效应明显，处理稀疏向量的能力弱，是协同过滤的天然缺陷。

矩阵分解——协同过滤的进化

矩阵分解加入了隐变量的概念，认为「共现矩阵」是有两个更小的矩阵乘得，一个是用户 embedding，一个是物品 embedding。

依据共现矩阵中已经存在的打分去训练得到两个小矩阵，反向推导得到未知分数。假设共现矩阵为 m * n，那么两个小矩阵的形状为 m * k 和 k * n，k 一般远小于 m 和 n，具体由尝试得到。矩阵分解的求解方法也是梯度下降，两个小矩阵为变量，目标是乘积后的结果去接近共现矩阵中已经存在的打分。

矩阵分解的优势在于一定程度解决了稀疏问题，泛化能力强，而且将共现矩阵退化为两个小矩阵后，极大的节约了存储开支。**不足在于矩阵分解只能用于共现矩阵，**还有很多用户侧的画像信息、物品侧的信息都无法使用，单纯的矩阵分解无法使用其他特征。（但是分解后的结果可与其他特征组合

逻辑回归——能融合多种特征的简单模型

逻辑回归应该都比较熟了，假设数据分布符合伯努利分布，线性回归拟合对数几率，结果在0-1之间，可表示概率。

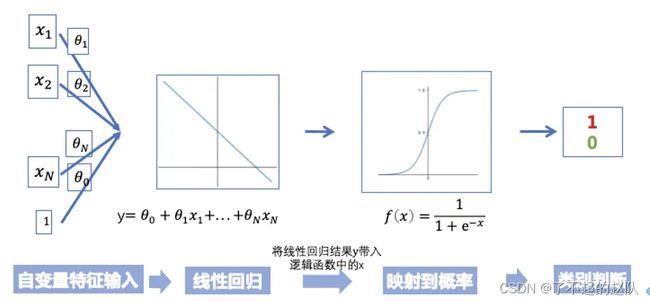
线性回归的优势在于不管啥特征，前期数据处理后一箩筐都能扔进去，而且可解释性强，每个特征一个权值，能直观的看出哪些特征起了主导作用。

逻辑回归的优势在于简单直观易用，不足在于表达能力有限，无法进行特征交叉，无法充分挖掘数据中的信息。

POLY2 —— 无脑特征交叉解决方案

poly2 在逻辑回归的基础上加入了特征交叉方案。

人工特征交叉一般会选择特定的一些特征进行手动交叉组合，这些交叉的特征一般也具有业务含义。poly2 选择无脑暴力全部交叉，组合所有可能，然后赋予不同的权值，权值是由训练得到。公式如下：
$$\varnothing \mathrm{P}\mathrm{O}\mathrm{L}\mathrm{Y}2(w,x)=\sum _{i_1=1}^n\sum _{j_2=i_1+1}^n{w}_{h\left(j_1,j_2\right)}{x}_{j_1}{x}_{j_2}$$最暴力的方法往往不是最好的，就如同把一张图片所有像素拍平用全连接神经网络其实不如卷机神经网络一样，这样组合所有的可能性，在特征稀疏时候（例如 one-hot）带来了训练上的困难，由于稀疏性提督也传不过来，很多权值缺乏有效的训练，造成收敛困难。

再一个是，这种组合方式实在是，太暴力了，参数数量对比逻辑回归直接平方增长，复杂度太高。

FM——借鉴了矩阵分解的特征交叉方案

FM 算法全称因子分解机，顾名思义，名字中带有分解，那肯定得分解啊。FM 算法借鉴了矩阵分解的思路，不想 poly2 那样儿，每个组合按一个权值，而是认为每个特征有自己权值，组合的权值是组员权值乘积。公式如下：
$$\varnothing \mathrm{F}\mathrm{M}(w,x)=\sum _{j_1=1}^n\sum _{j_2=j_1+1}^n\left(w_{j_1}\cdot w_{j_2}\right)x_{j_1}{x}_{j_2}$$同样，FM 也是在逻辑回归的基础上加入了特征交叉方案，只不过交叉方式没有那么暴力，如果将 poly2 的交叉权值比作上文中提到的「共现矩阵」，那么 FM 的交叉权值就是矩阵分解后的两个小矩阵，这样做的优点在于极大地减少了参数量，复杂度由 poly2 的 $n^2$ 变为$nk$（k为小矩阵的维度

看上去 FM 已经进化完全了，解决了之前的痛点，而且自身没有什么特别明显的硬伤。实际上也是这样，在深度学习到来之前，FM 基本上就是主流模型，即使后面有优化，也都是锦上添花的小操作。在 2012 - 2014 年前后，FM 就是主流的推荐模型之一。

FFM 模型——锦上添花，引入特征域

特征域这个东西，简单来说就是针对不同的特征有不同的权值。例如有 A、B、C 三个特征，按照 FM 的做法，在特征组合的地方，对应也有三个权值$W_A$、$W_B$、$W_C$，哪两个组合就哪两个权值相乘。

FFM 的变化在于针对不同的组合，有不同的权值。也就是说特征 A 不只有一个权值，而是针对特征 B 有一个，针对特征 C 也有一个，不同的组合选择对应的权值。

其实还是利用复杂度和参数量换取更多的特征组合后的表达能力，到底算不算进步这个见仁见智吧。

从 poly2 到 FFM，一路过来都是在追求特征组合的性价比，在性能和代价之间做一个平衡。如果非说 FM 系列算法有什么硬伤的话，那就是没办法进行三阶特征组合，因为组合的数量就爆炸了。

GBDT + LR —— 高阶组合与自动筛选

树模型由于其优越的机制天生拥有特征筛选和高阶组合能力，将树模型的结果作为逻辑回归的输入，最终目标转化为预估 CTR，这是直观上 make sense 的想法。

首先来说 GBDT 的部分，GBDT 使用的是回归树，如果要转变成分类问题，可以借鉴逻辑回归的 loss，如下：
$$L=\arg \min \left[\sum _i^n-\left(y_i\log \left(p_i\right)+\left(1-y_i\right)\log \left(1-p_i\right)\right)\right]$$ GBDT 的训练目标仍然是 CTR 预估，最终生成 N 棵树后，将数据落入的叶子节点的位置置1，其余位置置0，拼接成0/1向量进入下一阶段的逻辑回归。

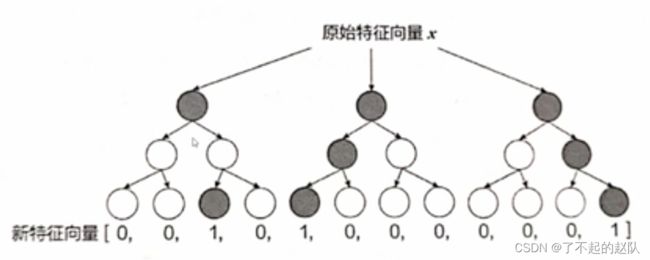
如上图所示，0/1特征进入逻辑回归后正常训练二分类即可。上图中的例子其实已经是三阶特征组合之后的结果，更深的树则拥有更高的组合阶数。当然，逻辑回归中仍然有原始特征作为输入，组合特征是额外输入。这种两阶段的方式不必担心逻辑回归的提督如何向上传导至 GBDT 的问题，极为方便，GBDT 部分可以看作原始流程中的「特征工程」。

GBDT 这种特征交叉方式无疑是高阶的，但最后转换为 0/1 也损失了大量的信息，效果相比 FM/FMM 而言，也是见仁见智吧。它的重要贡献在于，实现了特征工程的自动化，实现了真正的端到端的训练。

LS-PLM —— 接近深度学习的推荐模型

LS-PLM 其实在 2012 年就被阿里巴巴作为主流推荐模型了，只不过在 2017 年才公布出来。

LS_PLM 的思路是将数据从业务层面分类后然后分别进行逻辑回归，分而治之。例如女性专用商品的场景就会排出男性用户的数据，以获得更干净准确的训练数据，其实就是多个 LR 作用在不用的业务域，这是一个纯业务上的 idea。而且在逻辑回归的后面，还加了 L1 和 L2 正则，不过这都是小的锦上添花。

在预测阶段，首先过一个分类模型，这里为softmax，然后根据不同类别的概率对不同域内的逻辑回归结预测的 ctr 结果进行融合，公式如下：
$$f(x)=\sum _{i=1}^m{\pi }_i(x){\eta }_i(x)=\sum _{i=1}^m\frac{e^{{\mu }_i\cdot x}}{{\sum }_{j=1}^m{e}^{{\mu }_j\cdot x}}\cdot \frac{1}{1+e^{-w_i\cdot x}}$$

逻辑回归本来就非常像一个最简单的神经网络，加上这种分而治之的策略，就更像神经网络 + attention 机制了，这也是深度学习来临之前最接近深度学习的一次。

深度学习纪元——大杀器来临

AutoRec —— 矩阵分解的NN版本

AutoRec 是一个自编码器，自编码器的含义就是，输入是自己，输出还是自己，模型的训练目标就是使得输入和输出尽可能相同，那么这样有什么意义呢？

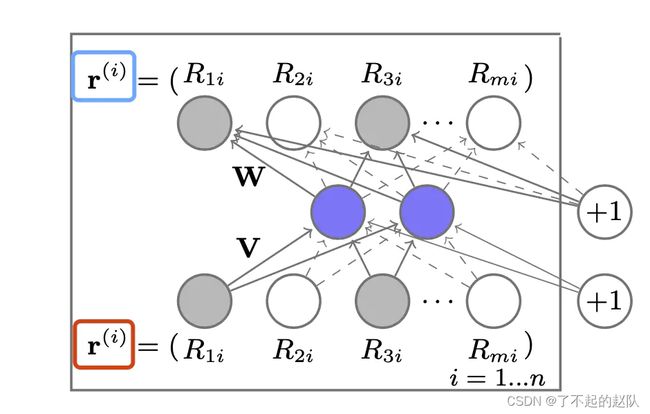
自编码器的结构其实就是简单的 MLP，当然，理论上别的结构也可以当编码器。应用在「共现矩阵」上，可以用来补足共现矩阵中缺失的分数。

利用无缺损的共现矩阵对网络进行训练，训练方式为一般的梯度下降。训练完成后输入带缺损的共现矩阵，缺失部分可以用默认值或者均值代替，然后输出中缺损位置的分数即为预测分数。

自编码器的输入与协同过滤相似，也可以分为基于物品和基于用户，本质上来说AutoRec 和 Word2Vec 差不多。AutoRec 是深度学习在推荐系统上的一次尝试，它的缺点仍然是只利用了共现矩阵的信息，但是终归是拉开了深度学习解决排序问题的序幕。

Deep Crossing —— 深度学习的经典应用

Deep Crossing 是微软用在 Bing 中的模型，应用场景涵盖搜推广。从现在的角度来看，Deep Crossing 就是一个经典的 MLP，但在当时也是一个很大的进步。

这个模型可能研发的比较早，但是在 2016 年才公之于众。首先是应用神经网络为特征的融合提供了便利，无论是离散特征、数值型特征，还是需要特殊编码的特征，只要能将其数字化，就可以作为网络的输入。

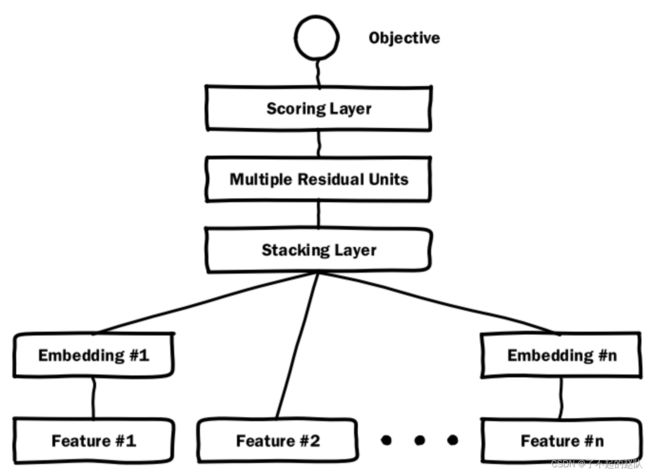
Deep Crossing 的结构非常简单，首先将特征进行 embedding 化，目的是把所有特征都变成稠密的embedding，以便后续处理；然后将各 embedding 拼接，这层叫做 stacking layer，名字很花哨，其实就是 concat；之后就是过几层 MLP，然后过一层 LR 将结果变为二值分类，如果有多分类需求则换为 softmax 即可，都是常规操作。

Deep Crossing 的优势在于利用了深度学习的特征交叉能力，相比 FM/FFM 等模型，特征交叉的阶数更深，而且非常便利的就可以完成端对端训练，这是深度学习第一次中规中矩的在排序模型中发光发热。（之所以说中规中矩是因为网络结构还是太太太太太常规了

Neural CF 模型 —— 矩阵分解思路与 NN 的结合

NCF 是 2017 年提出来的一个模型，尝试将深度学习与协同过滤结合起来。说到这里大家应该猜到了，与协同过滤结合，那还是只用了共现矩阵了，其他特征无法使用。但它仍然有自己的意义，探索了隐变量的交互方式，隐隐地有现在那些双塔模型的味道了。

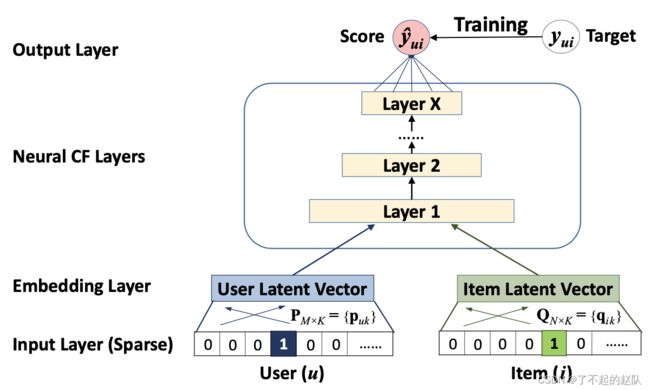
结构如上图所示，NCF 的思路是尝试用神经网络来描述矩阵分解，它提出了一个通用的框架，并提出了三种具体的实现方式。

第一种是 GMF（广义矩阵分解），其实就是矩阵分解。论文中证明了广义上的矩阵分解其实就是该种结构的一种特例，一种具体的实现方式。

假设$P_u$和$Q_i$分别代表 usr 和 item 的隐向量的话，那么第一层全联接层（即图中的 Neural CF layer）可以定义为：
$${\varphi }_1\left({\mathbf{p}}_u,{\mathbf{q}}_i\right)={\mathbf{p}}_u\odot {\mathbf{q}}_i$$其中$\odot$表示按元素位置乘积，之后再过一层输出层，整理得到公式为：
$${\hat{y}}_{ui}=a_{out}\left({\mathbf{h}}^T\left({\mathbf{p}}_u\odot {\mathbf{q}}_i\right)\right)$$ 这里也是常规操作啊，线性变化然后过一个激活函数。

第二种是多层全连接层，这个其实和上面刚刚说过的 Deep Crossing 有点像了，只不过 Deep Crossing 的输入为多种类特征，这里由于还是基于共现矩阵，所以输入为 usr 和 item 的隐向量。

输入之后，concat 起来经过多层 MLP，最终经过逻辑回归或者 softmax 得到分数，这里就不再赘述了。

第三种是上面两种的混合，两种方式有自己独立的 embedding 编码层，经过各自的机制之后，将结果拼接起来，最终通过逻辑回归或 softmax 得到分数。
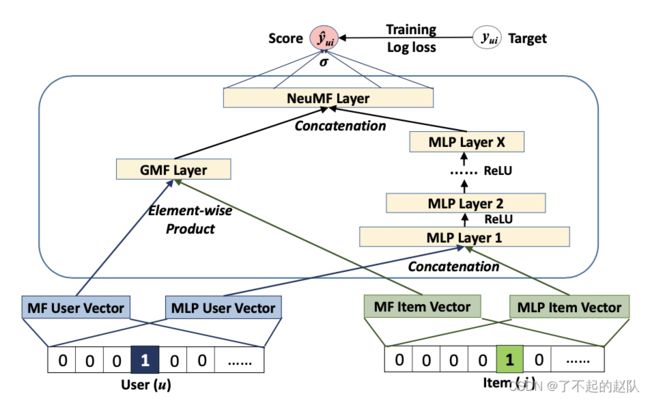这篇文章也是 2017 年提出的，显然作者是个比较怀旧的人，那个时候还揪着协同过滤那一套不放，没有意识到引入更多额外特征的作用，不过他也探索不同的特征交互方式。在身处在历史中的时候，能意识到变革的总是少数人。

PNN 模型 —— 进一步探索特征交叉

随着深度学习的到来，模型发展的契机也逐渐找到了路数——拥有更好的特征交叉能力，这样才能挖掘数据中更多的信息。

PNN（Product-based Neural Networks） 模型借鉴了 FM 的思路，将不同域内的 embedding 进行乘积，乘积后再经过 MLP，如下图所示。

PNN 由两个部分组成，线性部分，也就是直接对输入 embedding 进行拼接，对应图中的 z。乘积部分，对应图中的 p。关键就在乘积这一步，这里有两种乘积方式，内积和外积。

内积就不多说了，就是常规的矩阵的内积。矩阵内积之后显然会得到一个数字，所以embedding互相内积之后就变成了一个值，两两交叉之后就是多个值，这多个值组成向量，经历后面的网络。

外积可能一般不常用，用一个例子来说明。
外积就是穷尽所有组合的可能，矩阵中的每个值都相乘。这个外积看起来复杂度显然比较高，对后面网络层的参数也是暴增。PNN 的一个操作是将结果通过一个平均池化层来减小参数量，这个方法见仁见智吧。。。

PNN 模型在经过内积或者外积之后，并没有把结果直接送入全连接层，而是 z 部分的向量和 p 部分的向量各自自己先通过一个全连接层改变一下维度，改变一下参数量，然后再拼接输入之后的网络。不过这种操作也算常规操作，就不赘述了。

PNN 的优点显然在于探索了更多特征交互的可能性，局限性就是过于暴力了，无差别特征交叉。

Wide&Deep —— 浪潮之巅

Wide&Deep 是推荐系统中影响力非常非常大的模型，谷歌于 2016 年提出。顾名思义，这个模型就是又宽又深。当然「宽」和「深」是分为两个部分的，Wide 部分主要负责让模型具有较强的「记忆能力」，也就是机器学习中所说的，消除偏差，也就是说训练数据中出现过的你要预测对；Deep 部分的主要作用是让模型具有「泛化能力」，也就是机器学习中所说的消除方差，也就是说模型要具有一定的推理能力。没错，这是一个「既要又要」的模型。

Wide&Deep 是一个通用框架，论文中也给出了一种具体实现，模型的实现与验证基于谷歌 app 商城。

Wide 侧一般是一个线性模型，线性模型可以用非常少的参数量去记住训练数据中的信息。论文中 Wide 侧的实现是纯粹的线性模型，但是对输入有了些改变。Wide 侧的输入特征仅仅包含了「已安装 App」和「曝光 App」两类特征，并提出了一种交叉积变换的方式将其编码。交叉积变换的公式如下：
$${\varphi }_k(\mathbf{x})=\prod _{i=1}^d{x}_i^{c_{ki}}{c}_{ki}\in \{0,1\}$$
$k$表示第$k$个组合特征。$i$表示输入$X$的第$i$维特征。$C_{ki}$表示这个第$i$维度特征是否参与第$k$个组合特征的构造。这里是论文中最拗口的一段，但是其实非常简单。举个例子：

假设有两类特征，性别：男/女，衣服大小：大/中/小。

如果要表示「男、中」这个组合特征，顺序编码是啥？$[1,0,0,1,0]$，这个很好理解，我们规定向量排列含义为$[男，女，大，中，小]$，在命中的位置置1，就得到了如上结果。

如果要用 one-hot 的形式表示交叉特征呢？性别有 2 类，尺码有 3 类，交叉特征一定是 $2\ast 3=6$类，如下：
男 小 [1, 0, 0, 0, 0, 0]
男 中 [0, 1, 0, 0, 0, 0]
男 大 [0, 0, 1, 0, 0, 0]
女 小 [0, 0, 0, 1, 0, 0]
女 中 [0, 0, 0, 0, 1, 0]
女 大 [0, 0, 0, 0, 0, 1]
这个很好理解，one-hot 的常规操作，还是用「男 中」来举例，公式中的$k$表示的是组合后的特征种类数，这个例子中为 6，$x_i$则为原始特征的取值，原始特征指的是上面的 5 位数的特征，即$[1,0,0,1,0]$表「男 中」。$c_{ki}$表示原始特征中的当前属性有没有参与第 k 个组合特征。

我们一个一个来计算，当 k == 0 时，我们计算的是转换后的第 0 位，
原始特征$x=[1,0,0,1,0]$，i 为下缀
那么对应的$c=[1,0,1,0,0]$，因为，k == 0 对应组合特征「男 小」，只有「男」和「小」的位置可以置 1，其他为 0，那么套用公式：
$$1^1\ast 0^0\ast 0^1\ast 1^0\ast 0^0=0$$
所以计算得到第一个位置的数字为 0
如果我们按这个道理推广开来，会发现，组合特征的六个位置，只有第二个位置计算得到 1，其余都为 0，最终的结果即为 one-hot 之后的结果。所以说论文一般喜欢把简单的东西复杂化，这样看起来更加「学术」，其实就是一个组合 one-hot。

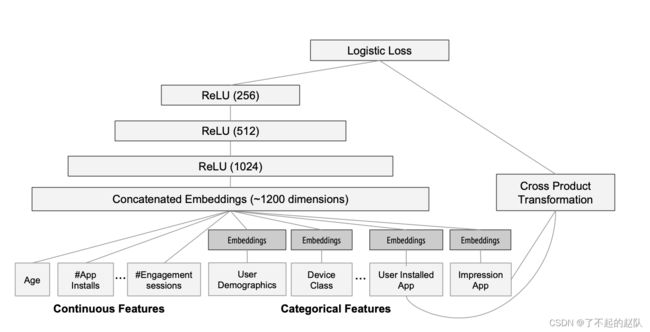
Deep 部分输入的是全量的特征，比如用户年龄、设备类型等等。这些特征按类别经过 embedding 后，concat 成一个 1200 维的大向量，然后依次经过三层 relu 全连接层，最终输入 LogLoss 输出层。

最终 Wide 侧的输出和 Deep 侧的输出一同决断整个模型的输出，公式如下：
$$P(Y=1\mid \mathbf{x})=\sigma \left({\mathbf{w}}_{wide}^T[\mathbf{x},\varphi (\mathbf{x})]+{\mathbf{w}}_{\text{deep }}^T{a}^{\left(l_f\right)}+b\right)$$这个公式比较简单，就不赘述了。

Wide&Deep 模型的 Wide 和 Deep 用的其实都是已经存在的东西，它胜在思路和机制，不仅综合了「记忆能力」和「泛化性能」，还没有对特征进行纯粹的暴力交叉，对比之前的模型属实是进步良多。最关键的是它提出了一种可以不断升级的框架，并不是一种特定的算法，后续模型也有很多是在不断改进模型的 Wide 侧或 Deep 侧。

Deep&Cross —— Wide 侧的优化

DCN 模型就是将 Wide 侧加入了更复杂的特征交叉机制，整体结构如下图：

左边的部分就是 Wide 侧改变后的样子，公式也如图中所示，将公式更详细的拆开来：

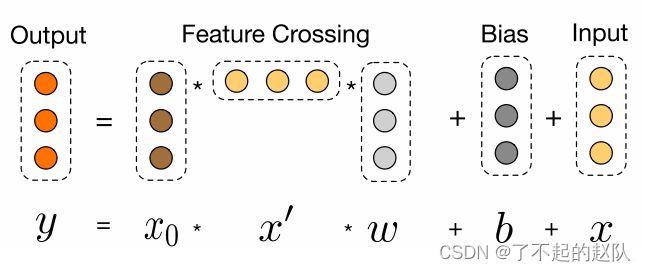
DCN 模型在增加参数方面是比较「克制」的，每一层仅仅增加一个 n 维向量，也就是图中的$\omega$，而且还类似残差网络一样在输出保留了输入，但是如果在高维向量的情况下，向量乘法计算时候的缓存还是比较高的。DCN 的局限之处有两点，一个是如果我们把特征交叉的公式稍加推导，就会发现，并不是每一组交叉特征的系数都是独立，这个可能会影响表达能力。第二点是如果输入的是 embedding，那么按照 bit 粒度去交叉，妥不妥？这个得实际试试才知道。

FNN —— 用 FM 隐向量初始化 embedding

FNN 也是 2016 年提出的，可能没赶上 Wide&Deep 的趟儿。FNN 是 FM 与深度学习的首次结合，为了引出后面的 Deep FM，所以放在这里来说。FNN 模型就是 FM 的隐藏层对 NN 的 embedding 层初始化，对应关系如下图
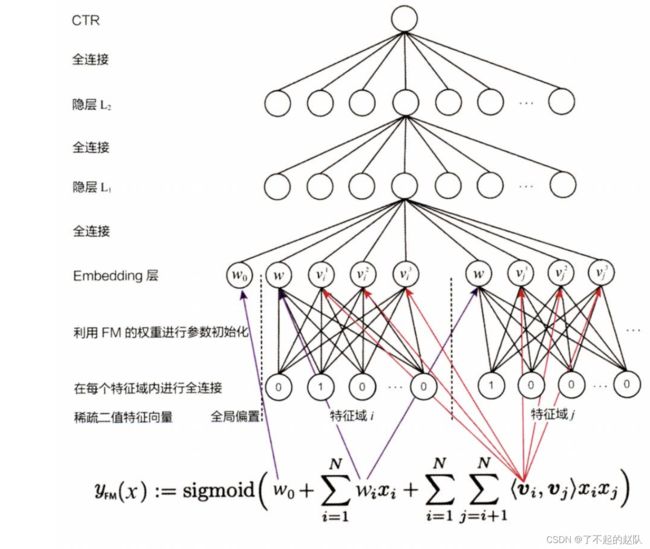只能说这是一次 FM 与 NN 的尝试结合吧，有点预训练的味道，但是最大的意义还是在于引出了一条思路，FM 与 NN 的结合。

DeepFM —— 用 FM 替代 Wide

DeepFM 就是用 FM 替代了 Wide 侧，结构如下图：

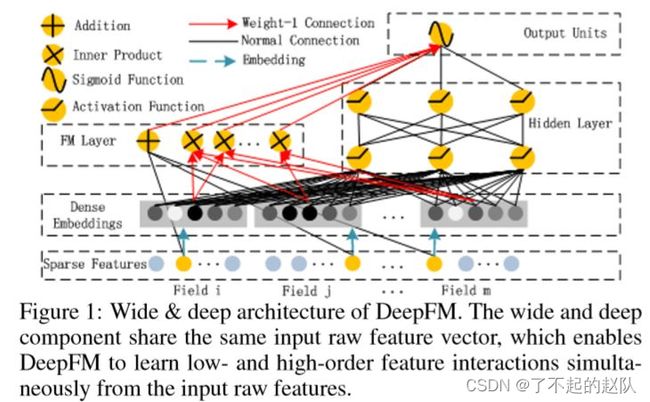
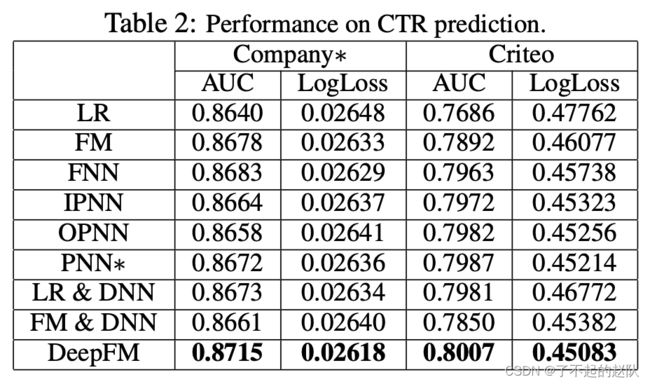
这里的改动思路与 Deep&Cross 是完全一致的，也是改善 wide 侧特征交叉的问题，两者的效果对比，其实没有明显的优劣，不同场景下都实验才能得到结论。对比其他算法，作者通过实验得出了结论，如下图：

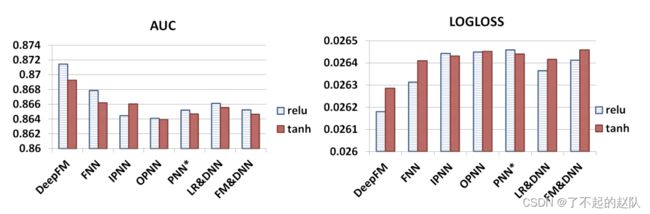
作者也通过实验证明了 relu 激活函数比 tanh 更适合 DeepFM (但在其他模型上效果不一)。

NFM —— FM 二阶部分改成 NN

NFM 也是 FM 与深度学习的一次结合，于 2017 年提出，将 FM 特征二阶组合的部分改成了神经网络，这样做的冬季动机仍然是提高特征交叉能力。也就是说，如果 FM 的公式是：
$${\hat{y}}_{FM}(\mathbf{x})=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n\sum _{j=i+1}^n{\mathbf{v}}_i^T{\mathbf{v}}_j\cdot x_i{x}_j$$那么 NFM 的公式为：
$${\hat{y}}_{NFM}(\mathbf{x})=w_0+\sum _{i=1}^n{w}_i{x}_i+f(\mathbf{x})$$其中那个$f(x)$就是神经网络，结构如下图：

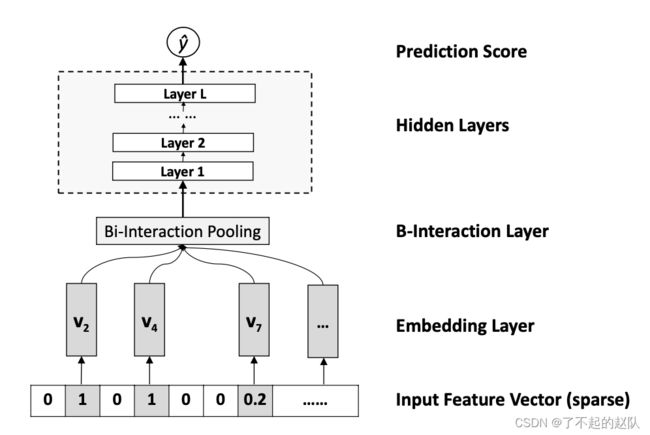
其主要创新就是在 embedding 层和 MLP 层之间加入了一层 b-interaction pooling layer，即特征交叉池化层，它的公式如下：
$$f_{BI}(V_x)=\sum _{i=1}^n\sum _{j=i+1}^n(x_i{v}_i)\odot (x_j{v}_j)$$其中$\odot$表示按元素位置乘，在进行两两 embedding 元素积之后，经过加和池化层（就是按位置多个向量加成一个），再进入之后的全连接层。

NFM 模型虽然表面上说是将 FM 与 NN 进行了结合，其实仔细一想其结合的结果也非常像 Wide&Deep 那个结构了，遗留下来的线性部分就是 Wide，改进后的 NN 部分就是 Deep。NFM 论文中自称效果要好于上述说过的那些模型。

AFM —— Attention 机制 + FM

Attention 机制在 CV 和 NLP 里大放异彩，因为它直观理解上就非常适合这两个领域，不过在排序上也可以应用。

AFM 可以看作上面 NFM 的一个改进，改进了加和池化层。加和池化层是众生平等地加和，显然有权重的加和更好，权重是多少自然是训练出来的，从这个思路想过来，自然是加一个 attention 机制更好了。这里的Attention 机制没有什么特别的地方，就不赘述了。

DIN —— 阿里的业务侧优化，深挖用户兴趣

DIN 是一个完全业务侧的想法，基于广告的场景提出了优化。base 模型如下：

简化一下来说，输入的特征分为两部分，「用户特征」和「候选广告特征」，常规操作的话就是如上图所示，embedding 之后利用池化层搞成固定长度的向量，拼起来过后面的 MLP。其中「用户特征」中一般会输入历史点击过的「商品id」和「商铺id」，也就是用户点击过的商品合集，base 模型的问题就在于这部分特征没有经过权重的加成，直接一视同仁的进入池化层了。DIN 的主要优化点就是在这里加入了 Attention 机制，结构如下图：
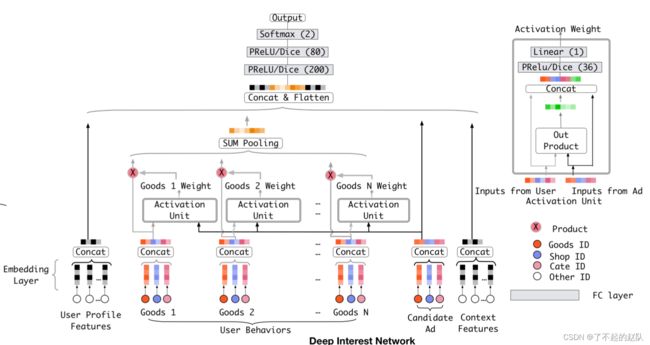那么这个注意力应该怎么计算？论文中给出的答案是计算「候选广告」和「已点击商品序列」的相关性，其相关性的大小就是 Attention 的大小，这是非常 make sense 的。直观上，人们愿不愿意点这个广告，是根据人的兴趣，而兴趣其实就体现在历史点击的商品序列中。注意力机制的设计结构如图中右上角所示，将两个原始向量和二者的外积拼接后输入，经过 MLP 得到分数。一般应用时可以更加细化，比如历史的商品 id 只跟候选的广告商品 id 发生 attention，商铺只跟商铺 id 发生 attention。

DIN 相比以前的模型来说，是典型的业务驱动的一次改进。

多目标侧的模型

排序模型侧还有一个角度的发展，与之前的「特征交叉」、「深度学习」之类的发展动机都不一样，那就是多目标训练。一般业务下模型训练是需要满足多个目标的，比如推荐场景下同时兼顾 ctr 和 cvr，或者搜索场景下同时兼顾点击、点赞、收藏等等。多目标的模型就介绍以下两个比较常用的吧。

ESMM

ESMM 又是阿里的一次业务驱动创新了，动机是为了解决推荐场景下训练数据与推理数据分布不一致和数据稀疏的问题。

先说第一个问题，在推荐系统、在线广告等应用中，CVR预估比CTR预估更加重要，CTR预估聚焦于点击率预估，即预测用户会不会点击，但是用户点击后进行消费才是最终目标。
转化是在点击之后发生，传统CVR预估模型在clicked数据上训练，但是在推理时使用了整个样本空间见图。训练样本和实际数据不服从同一分布，不符合机器学习中训练数据和测试数据独立同分布的假设。直观的说，会产生转化的用户不一定都是进行了点击操作的用户，如果只使用点击后的样本来训练，会导致CVR学习产生偏置。

第二个问题数据稀疏就很好理解了，常见问题。

ESMM 结构如下图：
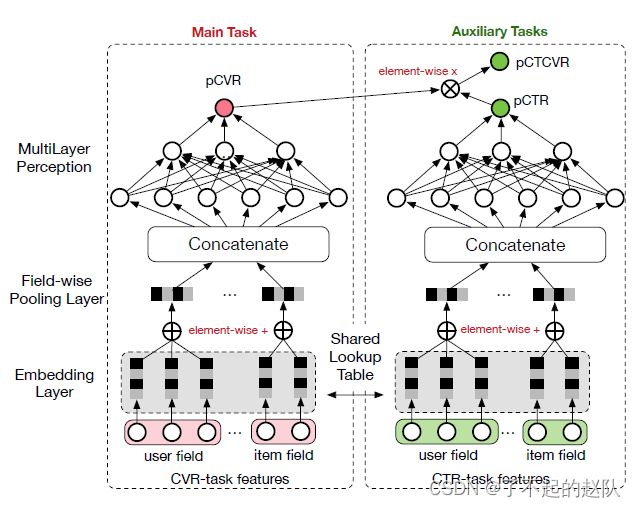首先明确CTR、CVR、CTCVR。CTR表示点击率、CVR表示假设用户点击后的转化率、CTCVR表示用户点击并且成功转化。绿色部分是常规的监督学习，红色部分是中间变量，与其他两个是能通过乘法互相转化，所以通过监督学习另外两个目标，就可以得到中间变量。

可以看出在 ESMM 中，CVR 与 CTR 任务共享Embedding 参数。这种参数共享机制使 ESMM 中的 CVR 网络可以从未点击的样本中学习，在一定程度缓解了数据稀疏性问题。

MMoE

MMoE 可以简单认为 shared bottom model 与 one gate moe 的结合。先来介绍第一种，shared bottom model，结构如下图：

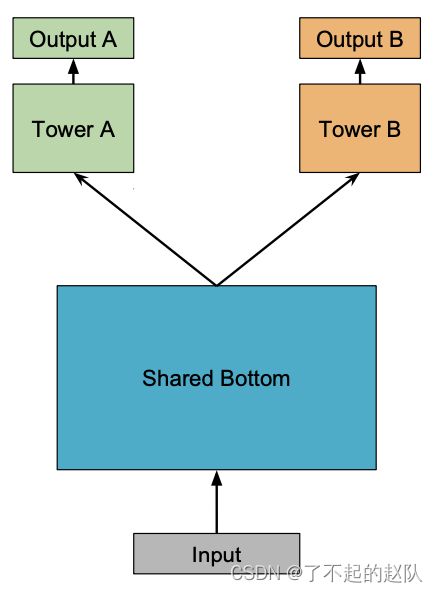
其实顾名思义，这个多任务结构底层是共享的，上层根据不同任务有自己的塔（参数）。这种结构要求多个任务之间相似，而且一旦出现任务间目标的互斥，有可能会出一些问题。

one gate Moe 的结构如下：

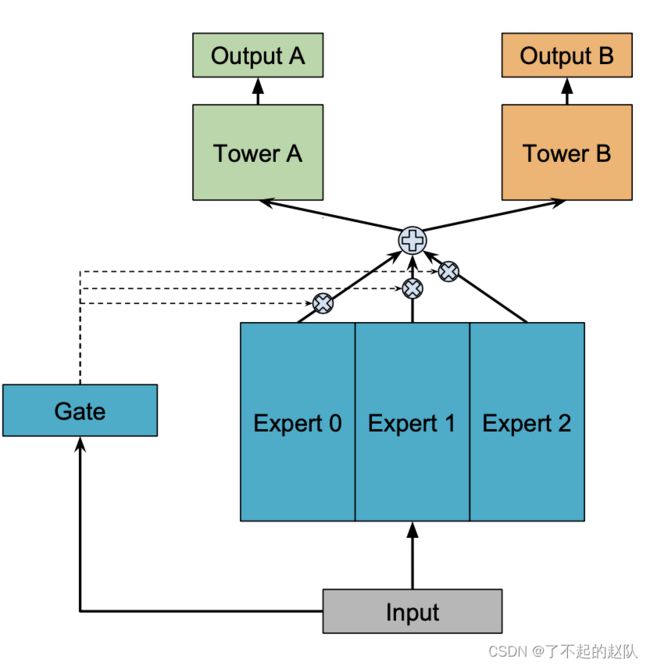
这个结构同样是有共享层的，只不过在共享层中，有多个专家，每个专家层相当于一个多层神经网络，多个专家层就是多个多层网络，这些网络都属于共享层，由下游的不同task共同享用；

然后该模型中还添加了门控层：Gate层。Gate层是一个浅层的神经网路，最后经过softmax层，输出的是k个标量，给每个expert专家层分配一个权重参数，所有权重参数之和等于1；

gate层可以理解为一个简单的 attention model，即给每个专家层分配不同的注意力权重。

将两者结合的话，MMoE 结构如下：

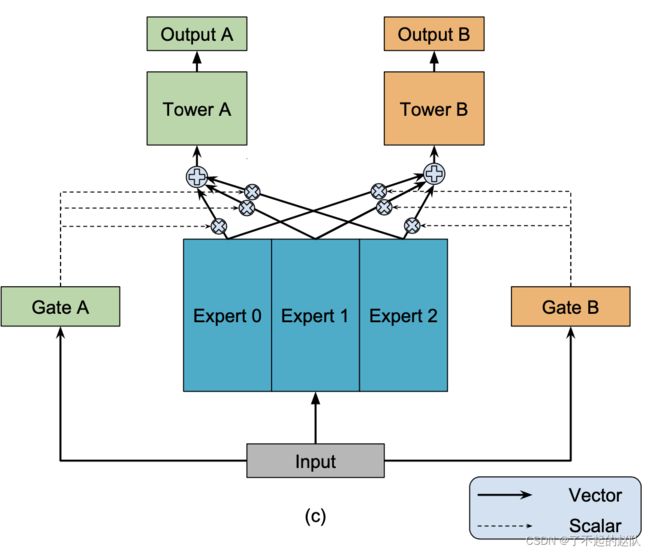
最大的不同是多个 gate，多个 gate 的优势就是不同的任务直接可以利用不同权重的专家网络输出的信息。

凡是过往，皆为序章

算法的每一个细分领域拆开来都是一本历史书，CV如此，NLP也是如此，每一次的进步或是体现了业务上的灵感，或是体现了人类的想象力，又或者是因为站在巨人的肩膀人。

站在前人的肩膀上，未来一定会有更强的机制出现，可能现在已经出现或者说在逐步应用推广的强化学习，是时代的弄潮儿吧。