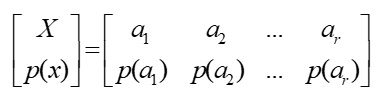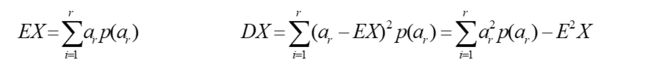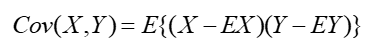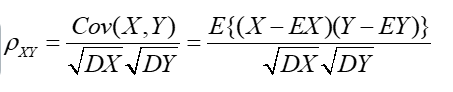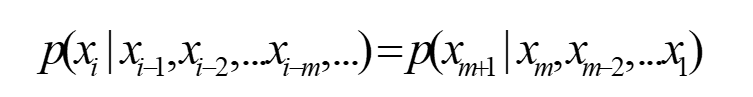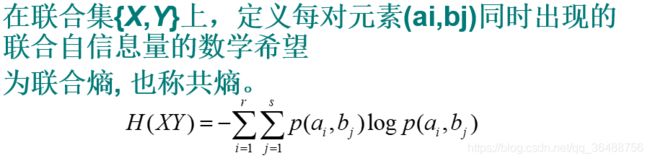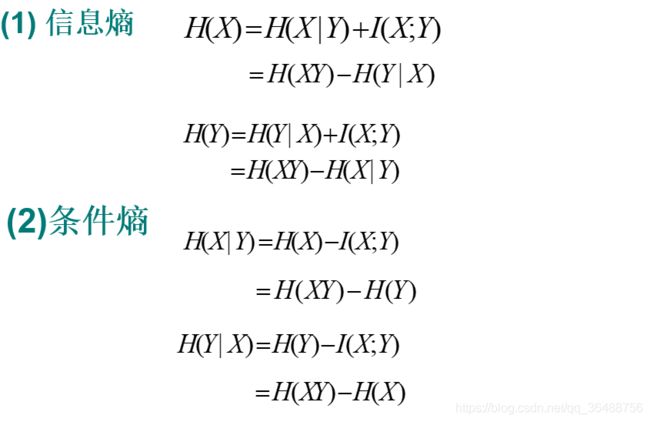信息论——信源信息量和信息熵
目录
一、概率基础知识
二、信源信息量和信息熵
离散有记忆信源
信源的随机性
信息量大小
自信息量;该符号出现后,提供给接收者的信息量,表示信源符号的先验不确定性
事件之间的互信息量:事件与事件之间的互信息量之所以存在,是因为两者之间存在相关,
条件自信息量:
联合自信息量
自信息量、互信息量、事件自信息量的计算举例
信息熵
信源熵:
条件熵:观测到集合Y后,集合X保留或者剩余的不确定性。
联合熵:事件X,Y同时发生的不确定性
互信息量(交互熵):接收到Y后,所得到的关于X的信息量,或者X的不确定性减少量
各类熵之间的关系
一、概率基础知识
概率空间:
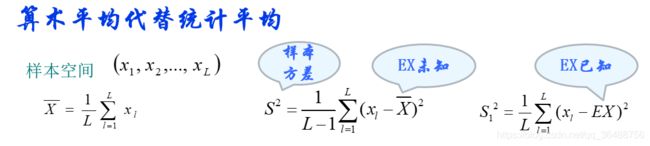
均值 , 方差(是随机变量围绕均值分布离散程度的测度,或者说是随机变量混乱程度的一种测度。)
协方差
相关系数(反应变量相关程度的指标)
二、信源信息量和信息熵
信源分为离散信源(幅度和时间上都是离散的)和连续信源(时间上或者在幅度上是连续的)
根据消息符号之间是否关联还可分为有记忆信源(符号序列或者矢量)和无记忆信源(单个符号,也可以使用符号序列)
离散无记忆信源
可以用一个概率空间完全描述出来,即各个符号出现的概率一定,那么信源就确定了,信源一定,那么各个符号出现的概率就确定了,所以信源的消息符号及其概率分布完整地描述了信源的特性。
离散有记忆信源
当记忆长度为m+1时,即信源每次发出符号只与前m个符号相关,与更前面的符号无关,称这种信源为m阶马尔可夫信源。
如果条件概率与时间起点无关,这样的信源称为齐次马尔可夫信源 。
信源的随机性
1.某时刻输出符号是随机的,接收者事先不能确定
2.收到信息后可以消除或者减小这种不确定性(噪声,干扰存在,不能完全消除)
信息量
信息量定义应该遵循日常生活准则
(1)确定性事件,即P =1时,信息量应当为0;
(2)事件出现的概率越小,信息量应当越大;反之亦然;(Ø一个出现概率很小的符号,接收者事先很难猜测它是否会发生,而概率很大的符号,出现的可能性大,很容易猜测它的出现。)
(3)自信息量为非负的
(4)两个相互独立事件联合自信息量应等于它们各自两个信息量之和
按照上述准则,在函数空间寻找满足要求的函数来定义信息量
自信息量
该符号出现后,提供给接收者的信息量,表示信源符号的先验不确定性
注:
先验不确定性: 信源符号固有的
自信息量: 信源发出后该符号为接收者提供的信息量,是为了消除该符号不确定性,接收信息者需要获得的信息量
事件之间的互信息量:
事件与事件之间的互信息量之所以存在,是因为两者之间存在相关,
如果两者相互独立,则I(ai;bj)=0.
如果事件ai出现有利于事件bj的出现,那么I(ai;bj)>0
如果事件ai的出现不利于事件bj的出现,那么I(ai;bj)<0
条件自信息量:
在事件bj给定条件下 ,关于事件ai的不确定性 ;也是给定bj条件情况下,为了唯一确定ai的出现所必须提供的信息量。
I(ai|bj)较大时,则给出的关于事件ai出现保留较大的不确定性,反之就小。
![]()
联合自信息量
自信息量、互信息量、事件自信息量的计算
信息熵
自信息量反映了信源单个符号的先验不确定性,或者信源输出某一消息所包含的信息量,即信源单个消息符号信息量的大小;
信源输出的消息不同,各个消息符号对应的概率不同,所包含的信息量也就不同,所以它反映的只是具体输出消息符号的特性,不能够反映信源的总体特性,不能够作为信源的信息度量,只是单个符号的信息度量。
下面讨论信源的总体不确定性,或者每输出一个消息符号所能够提供的信息量平均值,即平均信息量,也称为熵。
熵
定义自信息量的数学期望为信源的平均自信息量,也称为熵
当p=0.5时,即两个符号出现概率相等时,对应的熵最大,H(x)=1比特/符号;由于p=0.5时,两个符号输出的概率相等,信源没有输出之前,很难猜测哪个消息会出现;
当p<0.5时,出现的概率较大,比较容易猜中a2,所以提供的信息量少。尽管a2信息量较大,但由于出现概率小,出现的次数较少, 综合起来,信源的不确定性小
信源熵:
对于信道传输而言,信源熵只是反映了信源平均先验不确定性,一般情况下,并不等于信宿获得的平均信息量,只有在理想信道,即无噪声干扰情况下,信宿才能准确接收信源发出的消息,从而完全消除平均不确定性,获得的信息量的均值为H(X)。
条件熵:观测到集合Y后,集合X保留或者剩余的不确定性。
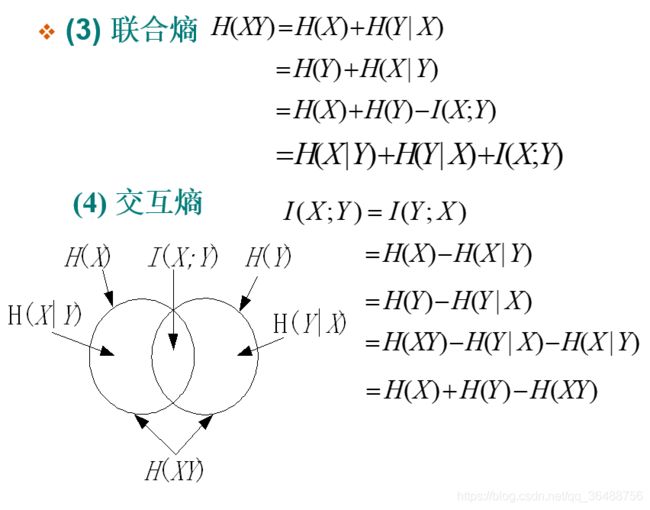
联合熵:事件X,Y同时发生的不确定性
互信息量(交互熵):接收到Y后,所得到的关于X的信息量,或者X的不确定性减少量
各类熵之间的关系