HDU 4365 Palindrome graph

题意：给你n*n的方格纸，在格子里填颜色,要满足任意水平、垂直翻转后看到的图形都一样；

对于n*n的方格纸，则可填 (n/2+1)*(n/2)/2 种颜色，如图。

 

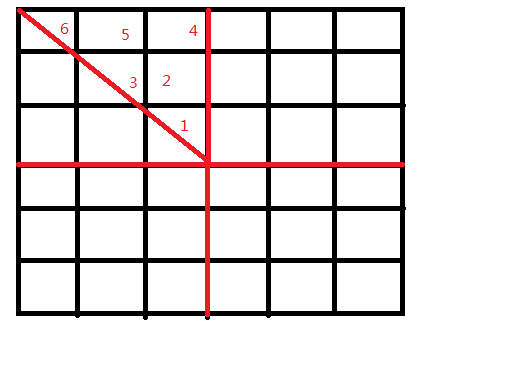
我们就只要涂图中的那个三角形即可，由于是对称的那么其余的方格也就确定了颜色;

 

有些方格已经填了颜色,对于已填色的方格，会固定对应格子的颜色，使得可填颜色数减1.注意多个已填色格本来就是同色格，不要多减因n范围比较大，不能直接开数组,我们就把所有的涂了颜色的方格的就过旋转之后来对应上面的三角形的方格，再去重就可以了，那么剩下了的方格，每个方格我们可以K种颜色；

 

 

View Code

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<algorithm>

#include<cmath>

#include<queue>

#include<set>

#include<map>

#include<cstring>

#include<vector>

#include<string>

#define LL long long

#define MOD 100000007

using namespace std;

class Point

{

public:

     int x,y;

     bool operator == (const Point &tmp) const{

        return  (x==tmp.x && y==tmp.y);        

     }    

}p[2024];

int midx,midy;

bool cmp(const Point &a,const Point &b){

    if(a.x != b.x)

    return a.x < b.x;

    return a.y < b.y;

}

void Solve1( int x, int y , int cnt )

{

    if( x > midx) 

    {

        x = (midx<<1) - x;

    } 

    if( y > midy ) y = (midy<<1) - y;

    if( x > y ) swap( x ,y );

    p[cnt].x = x; p[cnt].y = y;

}

void Solve2( int x, int y , int  cnt )

{

    if( x > midx )

    {

        int d = x - midx - 1;

        x = midx - d;

    }

    if( y > midy )

    {

        int d = y - midy - 1;

        y = midy - d;

    }

    if( x > y ) swap( x , y );

    p[cnt].x = x ; p[cnt].y = y;    

}

LL Pow( LL k , LL a )

{

    LL ans = 1;

    while( k )    

    {

         if( k &1 ) ans = (ans*a)%MOD;

         a = (a*a)%MOD;

         k >>= 1;    

    }

    return ans;

}

int main(  )

{

    int n,m,k,x,y;

    while( scanf( "%d %d %d",&n,&m,&k )==3 )

    {

           midx =  (n+1) /2;midy = midx;

           for( int i = 0; i < m ; i ++ )

           {

                scanf( "%d %d",&x,&y );

                x += 1 ; y += 1;

                if( n & 1 ) Solve1( x ,y , i );

                else Solve2( x , y , i );

//                printf( "%d %d\n",p[i].x,p[i].y );

           }

           LL L = ( n + 1 )/2;

           LL ans = L*L/2  + (L + 1) /2;

           sort(p,p+m,cmp);           

           ans -= unique(p,p+m)-p;

//           printf( "%I64d\n",ans );

           if( ans > 0 )

           {

           ans = Pow( ans , (LL)k );

           printf( "%I64d\n",ans ); 

           }

           else printf( "0\n" );    

    }

    //system( "pause" );

    return 0;

}