组合计数——车的放置(逆元)+数三角形+序列统计(lucas定理)

通用传送门：https://www.acwing.com/activity/content/16/

思路：设C(a,b)为从a中取出b个的组合数，设A(a,b)从a中选出b个进行排列的排列数。

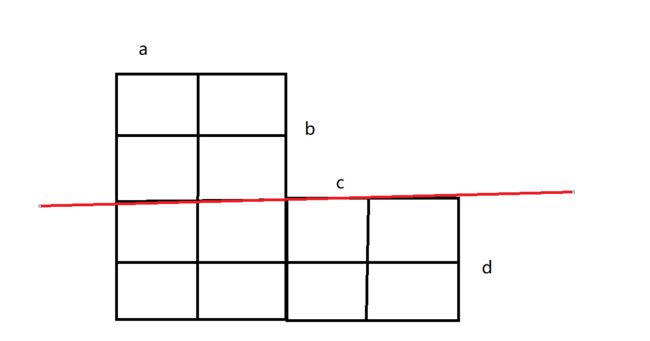
对于题目给的一个不规则的图形先用一个规则的矩形来分析，假设现在有一个a行b列的图形要按照题目要求放置k个车，并且是一定能够按要求放下。

首先从行中选择就是C(a,k)种方案，再来就是选择列，不能用组合的方法求，比如说现在是选择两列。已经选择了1,2,行，再选择了1,2列，一共放2个车，可以放两个对线，也就是有两种不同的方案，因此在选择列的时候要按照求排列数的方法也就是A(b,k)。

最终总结：在一个a*b的矩形里面放置k个车的方案数为C(a,k)*A(b,k)

回到原题中：

将原题的图形按照如下的方法切割，先放上面的矩形，再放下面的矩形，最后将上下方案数相乘，假设在上面放了i个车，那么下面的矩形就会有i列不能使用。

公式就是

至于i的大小枚举以一下就好了，最后将方案数相加。

代码：

#include
#include
#include
using namespace std;
typedef long long ll;
const int N=2e3+10,mod=1e5+3;
int fact[N],infact[N];//一个记录阶乘，一个记录逆元
int qmi(int a,int k)
{
    int res=1;
    while(k)
    {
        if(k&1) res=(ll)res*a%mod;
        a=(ll)a*a%mod;
        k>>=1;
    }
    return res;
}
int C(int a,int b)
{
    if(a>a>>b>>c>>d>>k;
    for(int i=0;i<=k;i++)
    {
        res=(res+(ll)C(b,i)*A(a,i)%mod*C(d,k-i)*A(a+c-i,k-i))%mod;;
    }
    cout<

传送门:数三角形

思路：对于这道题目，不能直接去找三个点可以摆放的位置，因为第三个点的可选数量会因为前两个点的选择位置不同而发生变化。所以这里就根据补集的定义，从所有的方案中减去不和法的方案数量即可。
先把n和m都自增1，因为下面要用的是能放点的数量而不是边的数量。
定义一个状态是不合法的状态当且仅当三个点处在同一条直线上。
从斜率的角度看
第一种情况：斜率为0的情况的，就是在每一行中找三个点一共有C(m,3),一共有n行，所以是n*C(m,3)。
第二种情况：斜率为正无穷的情况，与斜率为0的情况类似，一共有m*C(n,3)。

剩下的都是斜率绝对值大于0且非正无穷的情况，其中大于0和小于0的是对称的，所以只要是求出其中一种即可。这里采用的是枚举左下角和右上角的点的方法，中间的点就看两点之间整数点的数量。

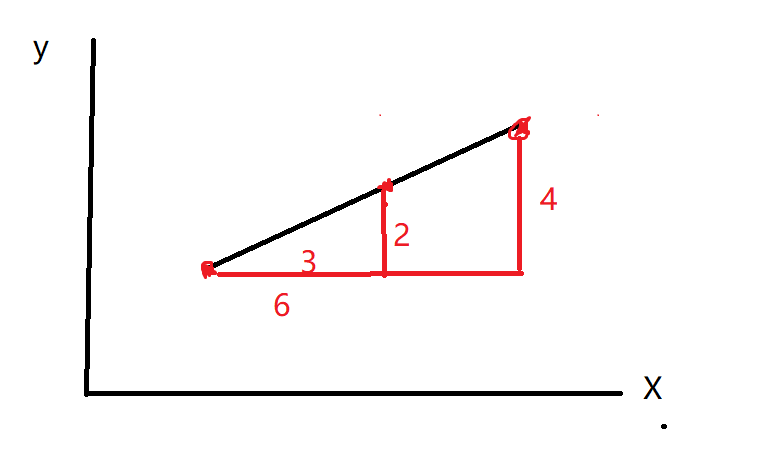
这里两点之间整数点的数量的公式是gcd(a,b)，其中a,b分别是两个端点的x坐标的差和y坐标差的绝对值。如下图所示：

只有两个直角边都是整数的相似三角形才会有一个点落在两个端点之间。此时有gcd(6,4)-1个点，就一个点。再比如边长为6,9,gcd(6,9)=3，故有两个点，也可以找到两个相似三角形的直角边分别是(2,3),(4,6).

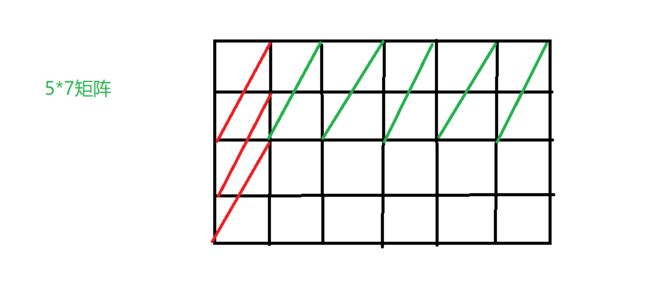
再来就是找到所有类型的边，比如(1,2)表示所有x方向上的投影为1，y方向上投影为2的一条线段，这条线段在这个n*m的矩形里面共有(n-1)*(m-2)条

 如下图的点数5*7矩阵所示，(1,2)的边能在y方向上找到3条，在x方向上找到5条，两者相乘就是15条，也就是说在这个5*7的矩阵里面可以找到15条斜率和长度相同但是位置不同的(1,2)的边。

代码:

#include
#include
#include
using namespace std;
typedef long long ll;
const int N=2e3+10,mod=1e5+3;

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}
ll C(int n)
{
    return (ll)n*(n-1)*(n-2)/6;  //这里是求C(n,3)
}
int main()
{
    int n,m;
    cin>>n>>m;
    n++,m++; //自增1变成点的数量。
    ll res=C(n*m)-(ll)n*C(m)-(ll)m*C(n);//总的数目减去斜率为0和斜率为正无穷的情况。
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        res-=2ll*(gcd(i,j)-1)*(n-i)*(m-j); //

        cout<

传送门：序列统计

思路：对于原问题就是枚举1~n个数，确定为k个数，

在l~r之间找到k个数使得这k个数满足

l<=a1<=a2<=a3<=..<=ak<=r，对于这个序列可以映射成一个单调递增的序列

l<=b1

映射完之后的序列b就是从r-l+k里面取k个数字，也就是C(r-l+k,k)。

对于长度为k的序列已经找到了一个取法算出长度为k的序列的数量，剩下的就是枚举k的大小。

至此完成第一步。

对于这条，经过杨辉三角公式进行变换之后就是C(r-l+n+1,r-l+1)-1

至于过程：.....

由于范围特别大，需要用到卢卡斯定理求组合数。

代码：

#include
#include
#include
using namespace std;
typedef long long ll;
const int N=2e3+10,p=1e6+3;
int qmi(int a,int k)
{
    int res=1;
    while(k)
    {
        if(k&1) res=(ll)res*a%p;
        a=(ll)a*a%p;
        k>>=1;
    }
    return res;
}
int C(int a,int b)
{
    if(a>n>>l>>r;
        cout<<(lucas(r-l+n+1,r-l+1)+p-1)%p<