深入理解warp shuffle

warp shuffle

相关函数学习：

__shfl_up_sync(0xffffffff, lane_val, i)是CUDA函数之一，用于在线程束内的线程之间交换数据。其中：

• 0xffffffff是掩码参数，指示线程束内所有线程都参与数据交换。一个32位无符号整数，用于确定哪些线程会参与数据交换。具体来说，若第 $i$ 位为1，则第 $i$ 个线程会参与交换，否则不参与。例如，若 mask 为 0x0f，则当前warp中的后四个线程会参与数据交换，前28个线程不参与。
• lane_val是要交换的数据，即当前线程的值。
• i是要向上移动的距离，即要将数据从当前线程的下一个线程移动到当前线程的位置。

__shfl_up_sync 函数会将当前线程 var 的值传递给与其向上 delta 个线程相隔的线程，而当前线程则接收到与其向上 delta 个线程相隔的线程的值，所以可以理解为该函数完成了两件事，一个是传递给下一个，另一个是该函数的值为被传递的值。
如果某个线程在 mask 中对应的位为0，则它不参与数据交换，即接收到的值为自身的 var 值。此外，如果向上移动 delta 个线程后，超出了当前warp的边界，则接收到的值为该线程的默认值（即0或者NaN）。

原理：
用下面这段代码做实验你会知道__shfl_down__syn函数的返回准则。

1、如果threadA，threadB，存在一个offset的距离，则一定是存到down的A中。
2、对于一个laneID，如果$A:laneID-offset>=0$则该线程的值将存到前offset那个线程的位置上。
3、对于一个laneID，如果$B:laneID+offset<WarpSize$ 意味着当前线程可以接受后offset那个线程的值。
4、如果A式<0则意味着，当前线程前面没有offset个单位，则不需要给任何线程赋值。
5、如果B式>=，则意味着，当前线程没有可以接受的值，那么函数返回的结果就是当前线程的值。
一张图理解：映射关系

#include 
__global__ void scan4() {
 
    int laneId = threadIdx.x & 0x1f;
    int val = 8 - laneId;

    for (int offset = 8 >> 1; offset > 0; offset >>= 1)
    {
       int n = __shfl_down_sync(0xff, val, offset, 8); 
       printf("Block id: %d Thread id :%d n value = %d\n", blockIdx.x, threadIdx.x, n);
    }
}
int main() {
    scan4<<< 2, 8 >>>();
    cudaDeviceSynchronize();
    return 0;
}

举个例子，假设当前线程束包含4个线程，它们的lane_id分别为0、1、2和3。
当调用__shfl_up_sync(0xffffffff, lane_val, 2)时，线程束内的线程会进行以下数据交换：

• 线程0和线程2之间交换数据。
• 线程1和线程3之间交换数据。

---

在早期的硬件上，只能通过使用共享内存，这就涉及将数据写入共享内存、同步，然后从共享内存中读取数据
Kepler 的 shuffle 指令 (SHFL) 使线程能够直接从同一个warp中（32 个线程）的另一个线程读取寄存器
用于在一个 warp（一个在单个处理器核上同步执行的线程组）内高效地重新排列数据。
Warp shuffle 允许 warp 内的线程互相交换数据，而不需要与 warp 外的线程通信，这可以显著降低通信的延迟和带宽需求。
同步发生在一个 warp 中并且隐含在指令中，因此不需要通过调用__syncthreads() 同步整个线程块。

1、warp shuffle 是对每个线程都有作用的。
2、但我们只需要关心我们关心的那部分
如图

// Sums `val` accross all threads in a warp.
//
// Assumptions:
//   - The size of each block should be a multiple of `warpSize`
template <typename T>
__inline__ __device__ T WarpReduceSum(T val) {
#pragma unroll
  for (int offset = (warpSize >> 1); offset > 0; offset >>= 1) {
    val += __shfl_down_sync(0xffffffff, val, offset, warpSize);
  }
  return val;
}

在 warp shuffle 算法中，使用二进制归约算法来实现在 warp 内快速计算数据的某些函数，例如前缀和、求最大值或最小值等。二进制归约算法的基本思想是，将相邻的两个元素两两配对，然后在每一轮迭代中将相邻元素的值累加，并重复这个过程，直到只剩下一个元素为止，这个元素即为最终的结果。因此，循环迭代的次数应该是以 2 为底数的对数，这也是为什么在循环中 i 是乘以 2 的原因。
在二进制归约中，我们希望每个线程将其值与距离其 2 的幂次方的线程的值相加。例如，在第一轮循环中，每个线程将其值与距离其 1 个位置的线程的值相加，第二轮循环中，每个线程将其值与距离其 2 个位置的线程的值相加，以此类推。
通过将 i 每次乘以 2，我们可以将循环次数减少到 $lo{g}_2(warpSize)$，其中 warpSize 是 warp 的大小。

在这段代码中，每个 warp 中的线程为输入数组的一个元素计算其自己的前缀和值，然后使用 warp shuffle 与相邻的线程交换值，以执行二进制归约以计算整个 warp 的最终前缀和值。__shfl_up_sync() 函数用于与左侧相距 i 个位置的线程交换数据，if 语句确保只有 ID 大于等于 i 的线程会参与归约z（因为小于i的线程没有线程给他传数，他函数返回值为自己，最后实现的是自己加自己的操作，没有意义）最后，warp 中的最后一个线程将最终的前缀和值存储在 prefix_sum 变量中。

用

线程 0 将得到最终归约的结果 v。下面这段代码就是完整的基于 shfl_down 的 warp reduction 函数。
__shfl_up_sync
The __shfl_sync() intrinsics permit exchanging of a variable between threads within a warp without use of shared memory.

Copy from a lane with lower ID relative to caller 把低的复制给高的

__device__ void warp_prefix_sum(int val, int& prefix_sum) {
    int lane_id = threadIdx.x % warpSize;
    int lane_val = val;

    for (int i = 1; i < warpSize; i *= 2) { //外层枚举从1开始
        int neighbor_val = __shfl_up_sync(0xffffffff, lane_val, i);
        if (lane_id >= i) { // 因为前面的没必要更新，因为更新的数据都是没用的，而且是不对的，没人跟他换他函数返回值是自己，相当于自己加自己，没什么意义！
            lane_val += neighbor_val;
        }
    }

    if (lane_id == warpSize - 1) {
        prefix_sum = lane_val;
    }
}

__shfl_down()
注意，如果 warp 中的所有线程都想要最终的规约结果，您可以在 warp 中使用 __shfl_xor() 指令替换 __shfl_down()，如下所示。任何一个版本都可以在下一节的 block reduce 中使用。

__inline__ __device__
int warpAllReduceSum(int val) {
  for (int mask = warpSize/2; mask > 0; mask /= 2) 
    val += __shfl_xor(val, mask);
  return val;
}

实验

实验1：

#include 

__global__ void scan4() {
    int laneId = threadIdx.x & 0x1f;
    // Seed sample starting value (inverse of lane ID)
    int value = 31 - laneId;

    // Loop to accumulate scan within my partition.
    // Scan requires log2(n) == 3 steps for 8 threads
    // It works by an accumulated sum up the warp
    // by 1, 2, 4, 8 etc. steps.
    for (int i=1; i<=4; i*=2) {
        // We do the __shfl_sync unconditionally so that we
        // can read even from threads which won't do a
        // sum, and then conditionally assign the result.
        int n = __shfl_up_sync(0xffffffff, value, i, 8); // 8 圈定了每8个thread一组
        if ((laneId & 7) >= i)
            value += n;
    }

    printf("Thread %d final value = %d\n", threadIdx.x, value);
}

int main() {
    scan4<<< 1, 32 >>>();
    cudaDeviceSynchronize();

    return 0;
}

这个算法的原理是这么个情况，如果是up就规约到最高，down就规约到最低。
一组：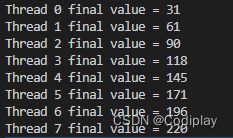
二组：

实验2：

#include 
__global__ void scan4() {
    int laneId = threadIdx.x & 0x1f;
    // Seed sample starting value (inverse of lane ID)
    int val = 8 - laneId;

    for (int i = 1; i <= 8 / 2; i ++ )
    {
       int n = __shfl_up_sync(0xff, val, i, 8); 
       if(laneId >= i) //加上 or 去除，体会不同
       {
        val += n;
        printf("Thread id :%d n value = %d\n val value: %d\n", threadIdx.x, n, val);
       }
    }
}
int main() {
    scan4<<< 1, 8 >>>();
    cudaDeviceSynchronize();
    return 0;
}

去除$if(laneId>=i)$后的实验

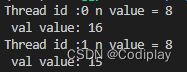
为什么1号是8？是因为1作为0号节点的接收对象，0节点给他传了0的值，为8。
这个地方就体现了，为什么0号thread的n也是8？是因为，第一个for循环中，0号节点没有作为up来接受的对象，所以函数返回为他自己。

实验太重要了！！！