MATLAB函数——fir1

fir1：基于窗函数法的 FIR 滤波器设计

---

语法

b = fir1(n,Wn)
b = fir1(n,Wn,ftype)

b = fir1(___,window)
b = fir1(___,scaleopt)

---

说明

b = fir1(n,Wn) 使用 Hamming 窗设计具有线性相位的 n 阶低通，带通或多频带 FIR 滤波器。滤波器的类型取决于 Wn 的元素数。举例

b = fir1(n,Wn,ftype) 根据 ftype 的值和 Wn 的元素数，设计一个低通，高通，带通，带阻或多频带滤波器。举例

b = fir1(___,window) 使用 window 中指定的向量和上述语法中的任何参数来设计滤波器。举例

b = fir1(___,scaleopt) 额外指定滤波器的幅度响应是否已归一化。

注意：

使用 fir2 设计具有任意频率响应的加窗滤波器。

---

示例

---

FIR 带通滤波器

设计一个通带为 0.35 $\pi ⩽\omega ⩽$ 0.65$\pi$ rad / sample 的 48 阶 FIR 带通滤波器。将其幅度和相位响应可视化。

b = fir1(48,[0.35 0.65]);
freqz(b,1,512)

---

FIR 高通滤波器

加载 chirp.mat。 该文件包含一个信号 y，其大部分功率都高于 Fs/4 或奈奎斯特频率的一半。 采样率为 8192 Hz。

设计一个 34 阶 FIR 高通滤波器，以衰减低于 Fs/4 的信号分量。使用 0.48 的截止频率和 30 dB 纹波的切比雪夫窗。

load chirp

t = (0:length(y)-1)/Fs;

bhi = fir1(34,0.48,'high',chebwin(35,30));
freqz(bhi,1)

对信号进行滤波。显示原始和高通滤波后的信号。两图都使用相同的 y 轴比例。

outhi = filter(bhi,1,y);

subplot(2,1,1)
plot(t,y)
title('Original Signal')
ys = ylim;

subplot(2,1,2)
plot(t,outhi)
title('Highpass Filtered Signal')
xlabel('Time (s)')
ylim(ys)

设计具有相同规格的低通滤波器。对信号进行滤波，并将结果与原始信号进行比较。两图都使用相同的 y 轴比例。

blo = fir1(34,0.48,chebwin(35,30));

outlo = filter(blo,1,y);

subplot(2,1,1)
plot(t,y)
title('Original Signal')
ys = ylim;

subplot(2,1,2)
plot(t,outlo)
title('Lowpass Filtered Signal')
xlabel('Time (s)')
ylim(ys)

---

多频带 FIR 滤波器

设计一个46阶FIR滤波器，该滤波器可以衰减低于 0.4$\pi$ rad / sample 和介于 0.6$\pi$ 和 0.9$\pi$rad / sample之间的归一化频率。将滤波器称为 bM。

ord = 46;

low = 0.4;
bnd = [0.6 0.9];

bM = fir1(ord,[low bnd]);

重新设计 bM，交换其通带和阻带。将新的滤波器称为 bW。 使用 fvtool 显示滤波器的频率响应。

bW = fir1(ord,[low bnd],'DC-1');

hfvt = fvtool(bM,1,bW,1);
legend(hfvt,'bM','bW')

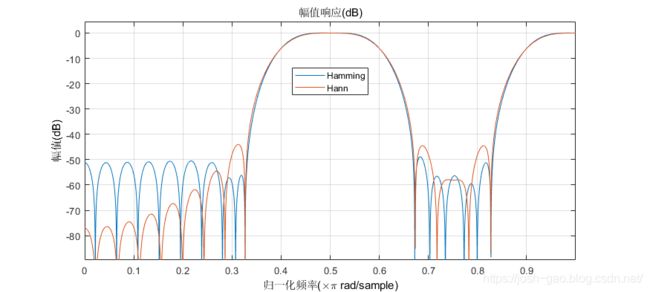
使用 Hann 窗重新设计 bM。 （DC-0 是可选的。）比较 Hamming 窗和 Hann 窗设计的幅度响应。

hM = fir1(ord,[low bnd],'DC-0',hann(ord+1));

hfvt = fvtool(bM,1,hM,1);
legend(hfvt,'Hamming','Hann')

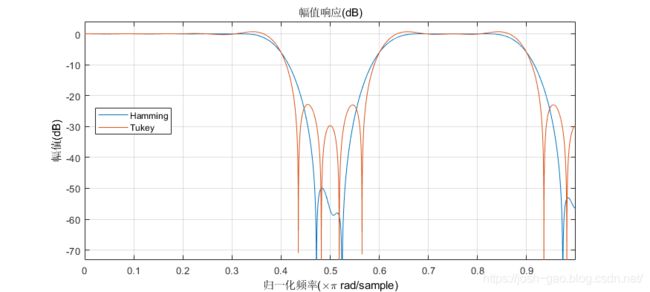
使用 Tukey 窗重新设计 bw。 比较 Hamming 窗和 Tukey 窗设计的幅度响应。

tW = fir1(ord,[low bnd],'DC-1',tukeywin(ord+1));

hfvt = fvtool(bW,1,tW,1);
legend(hfvt,'Hamming','Tukey')

---

输入参数

---

n - 滤波器阶数

滤波器阶数，指定为整数标量。

对于高通和带阻滤波器，fir1 始终使用偶数阶滤波器。此时阶数必须是偶数，因为奇数阶对称 FIR 滤波器在奈奎斯特频率下必须具有零增益。如果为高通或带阻滤波器指定奇数 n，则 fir1 将 n 增加 1。

数据类型：double

---

Wn - 频率约束

频率约束，指定为标量，二元向量或多元向量。

Wn 的所有元素必须严格大于 0 且严格小于 1，其中 1 对应于奈奎斯特频率：0 < Wn <1。奈奎斯特频率是采样率的一半或 $\pi$ rad / sample。

• 如果 Wn 是标量，则 fir1 设计一个截止频率为 Wn 的低通或高通滤波器。截止频率是滤波器的归一化增益为 –6 dB 的频率。

• 如果 Wn 是二素向量 [w1 w2]，其中 w1 < w2，则 fir1 设计一个具有较低截止频率 w1 和较高截止频率 w2 的带通或带阻滤波器。

• 如果 Wn 是多元素向量 [w1 w2 ... wn]，其中 w1 < w2 < …< wn，则 fir1 返回频带为 0 < $\omega$ < w1，w1 < $\omega$ < w2，…，wn < $\omega$ < 1 的 n 阶多频带滤波器。

数据类型：double

---

ftype - 滤波器类型

滤波器类型，指定为以下之一：

• 'low' 指定一个截止频率为 Wn 的低通滤波器。'low' 是标量 Wn 的默认值。

• ‘high’ 指定一个截止频率 为 Wn 的高通滤波器。

• 'bandpass' 指定一个带通滤波器，如果 Wn 为二元向量。 当 Wn 具有两个元素时，默认设置为 'bandpass'。

• 'stop' 指定一个带阻滤波器，如果 Wn 为二元向量。

• 'DC-0' 指定第一频带为阻带的多频带滤波器。 当 Wn 具有两个以上元素时，默认设置为 'DC-0'。

• 'DC-1' 指定第一通带为阻带的多频带滤波器。

---

window - 窗

窗，指定为向量。 窗向量必须具有 n + 1 个元素。 如果未指定窗，则 fir1 将使用 Hamming 窗口。 有关可用窗的列表，请参见加窗法。

如果尝试设计奇数阶的高通或带阻滤波器，则 fir1 不会自动增加窗的长度。

举例：kaiser(n+1,0.5) 指定一个用于 n 阶滤波器的成型因子为 0.5 的 Kaiser 窗。

举例：hamming(n+1) 等价于未指定窗。

数据类型：double

---

scaleopt - 归一化选项

归一化选项，指定为 'scale' 或 'noscale'，默认为 'scale'。

• 'scale' 对系数进行归一化，以使通带中心处的滤波器幅度响应为 1（0 dB）。
• 'noscale' 不对系数进行归一化。

---

输出参数

---

b - 滤波器系数

滤波器系数，以长度为 n + 1 的行向量返回。这些系数以 Z 变换变量 $z$ 的降幂排序：
$\mathbf{B}(z)=$ b(1) + b(2)$z$ + … + b(n+1)$z^{-n}$

---

算法

fir1 使用最小二乘估计来计算滤波器系数，然后加窗来平滑脉冲响应。

---

参考

[1] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979, Algorithm 5.2.

---

扩展功能

---

C/C++ 代码生成

使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

---

另请参阅

cfirpm | designfilt | filter | fir2 | fircls | fircls1 | firls | firpm | freqz | hamming | kaiserord

---

在 R2006a 之前推出

---

原文参考：https://ww2.mathworks.cn/help/signal/ref/fir1.html