xmu 离散数学 卢杨班作业详解【4-7章】

第四章 二元关系和函数

4.

A={1,2,3}

恒等关系

$I_A=\{<1,1>,<2,2>,<3,3>\}$

全域关系$E_A=\{<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>\}$

小于等于关系

$L_A=\{<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,<3,3>\}$

整除关系

$D_A=\{<1,1>,<1,2>,<1,3>,<2,2>,<3,3>\}$

6.2

A={1,2,4,6}，列出R

R={(x,y)|x,y$\in$A$\wedge$ |x-y|=1}

$R=\{<1,2>,<2,1>\}$

9

$R=\{<0,1>,<0,2>,<0,3>,<1,2>,<1,3>,<2,3>\}$

求R$\circ$R，$R^{-1}$

$R\circ R=\{<0,2>,<0,3>,<0,3>,<1,3>\}$

$R^{-1}=\{<1,0>,<2,0>,<3,0>,<2,1>,<3,1>,<3,2>\}$

11

设$A=\{1,\mathrm{2...10}\}$

$R=\{<x,y>|x,y\in A\wedge x+y=10\}$

对称性，非自反性(含$<5,5>$)

12

关系图：

关系矩阵：
[ 0 1 2 3 0 1 0 0 1 1 0 0 0 0 2 1 1 0 1 3 0 0 1 0 ] \left[ \begin{matrix} & 0 & 1&2&3 \\ 0 &1&0&0&1 \\ 1&0&0&0&0 \\ 2&1&1&0&1\\ 3&0&0&1&0\\ \end{matrix} \right] ​0123​01010​10010​20001​31010​ ​

16

$ 自反闭包：r®=R\cup R^0$

$对称闭包:s(R)=R\cup R^{-1}$

$传递闭包:t(R)=R\cup R^2\cup ...$

18.1

是$Z^{+}$ 的划分

1. $\varnothing$ $\notin$ $\pi$

2. S1，S2不交

3. S2=$Z^{+}$-S1=$Z^{+}$$\cap$ ~S1

   S1$\cup$S2=($Z^{+}$$\cap$~S1)$\cup$S1=($Z^{+}$$\cup$ S1)$\cap$(~S1$\cup$S1)=$Z^{+}$

20.2

22.1

极大元：e

极小元：a

最大元：e

最小元：a

23

蓝色圈住的地方为B

上界：12

下届：1

最小上届：12

最大下届：1

28

回答是否为满射、单射、双射。若为双射，求反函数。求A在f下的像f(A)

为满射，单射，双射。

反函数为$f(x{)}^{-1}=<x,x-1>$

f(A)=6

非满射，非单射。

f(A)={1,2}

非满射，为单射

f(A)={1,$\frac{2}{3}$}

34

(1)

g$\circ$f=f(g(x))=f(x+4)=$(x+4{)}^2-2$

f$\circ$g=g(f(x))=g($x^2$-2)=$x^2$+2

(2)

g$\circ$f非单射，非满射，非双射

g$\circ$f非单射，非满射，非双射

(3)

g,h有反函数

$g(x{)}^{-1}$=x-4

$h(x{)}^{-1}$=$(x+1{)}^{\frac{1}{3}}$

第五章 代数系统的一般概念

2判断二元运算是否封闭

(2) 封闭

(4) 封闭

(8) 封闭

3

(2)不符合交换律、适合结合律。不符合分配律，分配律是两个二元运算之间的

(4) 不符合交换律，符合结合律。不符合分配律，分配律是两个二元运算之间的

(8) 适合交换律、结合律。符合分配律，乘法对加法适合分配律

4

(2) 无单位元（仅右单位元1），无零元，显然可得，无逆元

(4) 单位元为nxn的单位矩阵，零元为nxn的零矩阵。有逆矩阵的矩阵A的逆元为$A^{-1}$

(8) 加法：无单位元，无零元，显然可得，无逆元 //乘法：单位元为1,无零元，无逆元

8

(1)

1. 满足交换律：*、 $\circ$、$\bullet$
2. 满足结合律：*、$\circ$、$\bullet$ 、$\square$
3. 幂等：$\square$

(2)

*：没有单位元，零元为a，无逆元

$\circ$： 单位元为a，无零元，a的逆元为a，b的逆元为b

$\bullet$ ：无单位元，无零元，无逆元

$\square$： 无单位元(左单位元为a)，无零元(右零元为b)，无逆元

11

(2) S2构成V的子代数，S2对+,$\bullet$ 都是封闭的

12

设V1=({1,2,3},°，1)，其中x°y表示取x和y之中较大的数，V2=({5,6},*,6),其中x*y表示取x和y之中较小的数.

(1) 求出V1的所有子代数，其中哪些是平凡的子代数？哪些是真子代数？

(2)求积代数y,×y,给出积代数(V,×V,·,)的运算表和代数常数k,并说明k是什么特异元素

(1)

子代数系统的B的条件：

1. B$\subseteq$S
2. B$\notin$ $\varnothing$
3. B和S含有相同的子代数常数
4. B对V中所有运算封闭

1为单位元

B1={1},B2={1,2},B3={1,3},B4={1,2,3}

其中平凡子代数为：B1,B4

真子代数为：B2,B3

(2)

设$V_1\times V_2=<S1\times S2,\bullet ,k>$

$S_1\times S_2=\{<1,5>,<1,6>,<2,5>,<2,6>,<3,5>,<3.6>\}$

$<x_1,y_1>,<x_2,y_2>\in S_1\times S_2$

$<x_1,y_1>\bullet <x_2,y_2>=<x1\circ x_2,y_1\ast y_2>$

运算表：
[ < 1 , 5 > < 1 , 6 > < 2 , 5 > < 2 , 6 > < 3 , 5 > < 3.6 > < 1 , 5 > < 1 , 5 > < 1 , 5 > < 2 , 5 > < 2 , 5 > < 3 , 5 > < 3 , 5 > < 1 , 6 > < 1 , 5 > < 1 , 6 > < 2 , 5 > < 2 , 6 > < 3 , 5 > < 3 , 6 > < 2 , 5 > < 2 , 5 > < 2 , 5 > < 2 , 5 > < 2 , 5 > < 3 , 5 > < 3 , 5 > < 2 , 6 > < 2 , 5 > < 2 , 6 > < 2 , 5 > < 2 , 6 > < 3 , 5 > < 3 , 6 > < 3 , 5 > < 3 , 5 > < 3 , 5 > < 3 , 5 > < 3 , 5 > < 3 , 5 > < 3 , 5 > < 3 , 6 > < 3 , 5 > < 3 , 6 > < 3 , 5 > < 3 , 6 > < 3 , 5 > < 3 , 6 > ] \left[ \begin{matrix} &<1,5>&<1,6>&<2,5>&<2,6>&<3,5>&<3.6>\\ <1,5>&<1,5>&<1,5>&<2,5>&<2,5>&<3,5>&<3,5>\\ <1,6>&<1,5>&<1,6>&<2,5>&<2,6>&<3,5>&<3,6>\\ <2,5>&<2,5>&<2,5>&<2,5>&<2,5>&<3,5>&<3,5>\\ <2,6>&<2,5>&<2,6>&<2,5>&<2,6>&<3,5>&<3,6>\\ <3,5>&<3,5>&<3,5>&<3,5>&<3,5>&<3,5>&<3,5>\\ <3,6>&<3,5>&<3,6>&<3,5>&<3,6>&<3,5>&<3,6>\\ \end{matrix} \right] ​<1,5><1,6><2,5><2,6><3,5><3,6>​<1,5><1,5><1,5><2,5><2,5><3,5><3,5>​<1,6><1,5><1,6><2,5><2,6><3,5><3,6>​<2,5><2,5><2,5><2,5><2,5><3,5><3,5>​<2,6><2,5><2,6><2,5><2,6><3,5><3,6>​<3,5><3,5><3,5><3,5><3,5><3,5><3,5>​<3.6><3,5><3,6><3,5><3,6><3,5><3,6>​ ​
$k=<1,6>$

k是单位元

14

$$\begin{gathered} 若\psi 为V_1到V_2的同态 \\ V1=<S_1,\circ >(V{)}_2=<S_2,\ast > \\ 则\psi (x\circ y)=\psi (x)\ast \psi (y) \\ 普通加法和矩阵加法 \\ \psi (a)=\left[\begin{array}{cc}a& 0\\ 0& a\end{array}\right]\psi (bi)=\left[\begin{array}{cc}0& b\\ -b& 0\end{array}\right] \\ \psi (a)+\psi (b)=\left[\begin{array}{cc}a& b\\ -b& a\end{array}\right](+为矩阵加法) \\ 故可知\psi (a+bi)=\psi (a)+\psi (bi)(第一个+为普通加法，第二个为矩阵加) \end{gathered}$$

$$\begin{gathered} 普通乘法和矩阵乘法 \\ \psi (a\ast bi)=\left[\begin{array}{cc}0& a\ast b\\ -a\ast b& 0\end{array}\right] \\ \psi (a)=\left[\begin{array}{cc}a& 0\\ 0& a\end{array}\right] \\ \psi (bi)=\left[\begin{array}{cc}0& b\\ -b& 0\end{array}\right] \\ \psi (a)\ast \psi (b)=\left[\begin{array}{cc}0& a\ast b\\ -a\ast b& 0\end{array}\right] \\ 可知\psi (a\ast bi)=\psi (a)\ast \psi (bi)(第一个\ast 为普通乘法，第二个\ast 为矩阵乘法) \end{gathered}$$

故可知$\psi$为$V_1到V_2$的同态

不为单同态，因为对于*来说，$<a,b>和<b,a>的结果相同\psi (a\ast bi)=\psi (a)\ast \psi (bi)=\psi (b\ast ai)$

为满同态

不为同构

第六章 几个典型的代数系统

1.

(1)可结合、1为单位元、其中任何元素都有逆元。故为群

(4)lcm:最小公倍数 gcd:最大公约数。

可结合。对于lcm有单位元1，对gcd有零元1。在S不仅只有一个元素时，零元无逆元。故为半群

(5)可结合。单位元为0。0的逆元为0，1的逆元为1；故其中任何元素都有逆元。为群

5.

可结合。2为单位元。其中任何元素都有逆元，为4-x。故可构成群

6.

(1)给出$\circ$运算表

$\circ$	f1=x	f2=$x^{-1}$	f3=1-x	f4=$(1-x{)}^{-1}$	f5=$(x-1)x^{-1}$	f6=$x(x-1{)}^{-1}$
f1=x	x	$x^{-1}$	1-x	$(1-x{)}^{-1}$	$(x-1)x^{-1}$	$x(x-1{)}^{-1}$
f2=$x^{-1}$	$x^{-1}$	x	1-$x^{-1}$	$(1-x^{-1}{)}^{-1}$	$(x^{-1}-1)x$	$x^{-1}(x^{-1}-1{)}^{-1}$
f3=1-x	1-x	$(1-x{)}^{-1}$	x	$x^{-1}$	$-1$	-1
f4=$(1-x{)}^{-1}$	$(1-x{)}^{-1}$	1-x	$1-(1-x{)}^{-1}$	$(1-(1-x{)}^{-1}{)}^{-1}$	x	$(1-x{)}^{-1}((1-x{)}^{-1}-1{)}^{-1}$
f5=$(x-1)x^{-1}$	$(x-1)x^{-1}$	$(x-1{)}^{-1}x$	$1-(x-1)x^{-1}$	x	$((x-1)x^{-1}-1)(x-1{)}^{-1}x$	$(x-1)x^{-1}((x-1)x^{-1}-1{)}^{-1}$
f6=$x(x-1{)}^{-1}$	$x(x-1{)}^{-1}$	$x^{-1}(x-1)$	$1-x(x-1{)}^{-1}$	$(1-x(x-1{)}^{-1}{)}^{-1}$	$(x(x-1{)}^{-1}-1)x^{-1}(x-1)$	x

可结合。f1为其单位元，所以元素都有逆元。故$<F,\circ >$ 是一个群

7.

(1)可结合，a为单位元，所有元素均有逆元。故$<G,\circ >$ 为群

(2)生成元有b,c。因为$b^k,c^k$涵盖了G里的所有元素

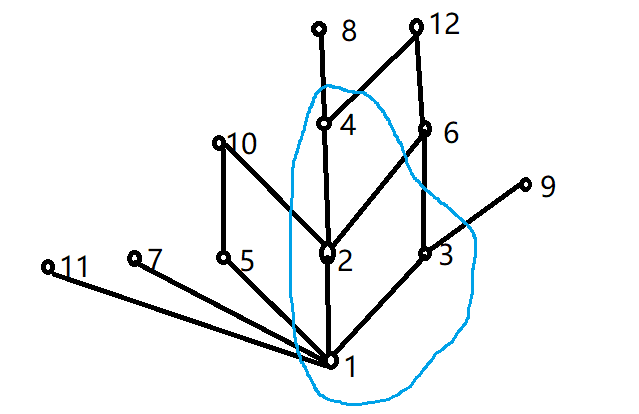
11.

$G=\{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19\}$

(1)所有生成元为：

n=20，生成元为小于等于20且与20互质的数

1 3 7 9 11 13 17 19

(2)G的所有子群

$G=<1>=<3>=<7>=<9>=<11>=<13>=<17>=<19>$（生成元的生成子群=G)

20的正因子为 1 2 4 5 10 20,故有6个子群

$H1=<0>=\{0\}$

$H2=<1>=G$

$H3=<2>=\{0,2,4,6,8,10,12,14,16,18\}=<20-2>=<18>$

$H4=<4>=\{0,4,8,12,16\}=<20-4>=<16>$

$H5=<5>=\{0,5,10,15\}=<15>$

$H6=<10>=\{0,10\}$

(3)[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FJb3ITaF-1678012348161)(课外学习资料/所需图片/QQ截图20221205145804.png)]

12

(1)

$\sigma =$(1 4 6 2 5 3 ),$\tau$=(1 3 2)(4 5 6)

(2)

$\sigma {\tau }^{-1}\sigma =(1,2,6)(3,5,4)$

${\sigma }^2=(1,6,5)(2,3,4)$

(3)

$\sigma$是6阶轮换，$\tau$是3阶轮换

15

(1)

由于已知为布尔代数，$\vee$对$\wedge$有可分配，$\wedge$对$\vee$也可分配

(a$\wedge$b)$\vee$(a$\wedge$b$\wedge$c)$\vee$(b$\wedge$c)$\vee$(a$\wedge$b$\wedge$c)

=((a$\wedge$b)$\wedge$(1$\vee$c))$\vee$((b$\wedge$c)$\wedge$(1$\vee$a))

=(a$\wedge$b)$\vee$(b$\wedge$c)

=b$\wedge$(a$\vee$c)

(2)

$f^{\ast }$=b$\vee$(a$\wedge$c)

16

18

根据 $\vee$对$\wedge$的分配律可得

a$\vee$(b$\wedge$c)=(a$\vee$b)$\wedge$(a$\vee$c)

又因为a《=c，故a$\vee$c=c

带入可得

a$\vee$(b$\wedge$c)=(a$\vee$b)$\wedge$(a$\vee$c)=(a$\vee$b)$\wedge$c

第七章 图的基本概念

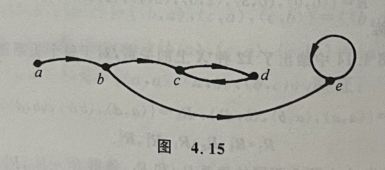
1

(1)

(2)

d(v1)=2

d(v2)=4

d(v3)=2

d(v4)=3

d(v5)=1

d(v6)=0

$\stackrel{6}{\sum _{i=1}}d(v_i)=2+4+2+3+1+0=12=2\ast 6=2\ast m$

(3)

奇度顶点的个数为2个。验证了：在任何图中，度数为奇数的顶点个数是偶数

(4)

无平行边。环为$e_2$ 。孤立点为$v_6$ 。悬挂顶点为$v_5$ 。悬挂边为$e_4$

(5)

多重图：含平行边

简单图：不含平行边也不含环

G无平行边，G不是多重图。G含环，G不是简单图

2

由握手定理。$\stackrel{6}{\sum _{i=1}}d(v_i)=2\ast m=24$。减去3*6度，还剩下6度，若剩下n-3个顶点均为2度时,n最小。计算可得G中至少有6个顶点

4

设：n阶无向图中，度数为k+1的顶点个数为x,度数为k的顶点个数为y。

由题可得

x+y=n

根据握手定理得

(k+1)*x+k*y=2*m

(k+1)*(x+y)-y=2*m

(k+1)*n-y=2*m

y=(k+1)*n-2*m

7

(1)

4阶自补图有一种非同构

5阶自补图有两种非同构

(2)

不存在3阶自补图：

3阶完全图一共有3条边。其生成子图，与其生成子图的补图，边数不同，不可能同构。

不存在6阶自补图：

6阶完全图一共有6*5/2=15条边。其生成子图，与其生成子图的补图，边数不同，不可能同构。

9

n为奇数，则n阶完全图每个顶点的度数为偶数。

若G中$v_i$ 的度数为奇数。根据补图的定义可得$d_G(vi)+d_{\bar{G}}(v_i)=d_{k_n}(v_i)$ ，n阶完全图每个顶点的度数为偶数。则若$\bar{G}$中$v_i$ 的度数为奇数。同理可推广至其他的点

可证，G与G的补图的奇度顶点的个数相等

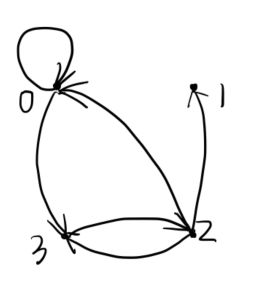
11

(1)

4条不同的初级回路:$c{e}_{3}c,e{e}_{2}d{e}_{1}e,bd{e}_{1}eb,baeb$

5条不同的简单回路:$c{e}_{3}c,ede,bdeb,beab,baedeb$

(2)

a到d的短程线为:$ae{e}_{2}d$，距离为$d<a,d>=2$

(3)

d到a的短程线为:$d{e}_{1}eba$，距离为$d<d,a>=3$

(4)

D是单向连通图

经过每个顶点至少一次的通路:$bae{e}_{2}dc$

12

D的邻接矩阵为
A 1 = [ 0 1 0 0 0 0 1 1 1 1 0 1 1 0 0 0 ] A^1=\left[ \begin{matrix} 0&1&0&0\\ 0&0&1&1\\ 1&1&0&1\\ 1&0&0&0\\ \end{matrix} \right] A1= ​0011​1010​0100​0110​ ​

A 2 = [ 0 0 1 1 2 1 0 1 1 1 1 1 0 1 0 0 ] A^2=\left[ \begin{matrix} 0&0&1&1\\ 2&1&0&1\\ 1&1&1&1\\ 0&1&0&0\\ \end{matrix} \right] A2= ​0210​0111​1010​1110​ ​

A 3 = [ 2 1 0 1 1 2 1 1 2 2 1 2 0 0 1 1 ] A^3=\left[ \begin{matrix} 2&1&0&1\\ 1&2&1&1\\ 2&2&1&2\\ 0&0&1&1\\ \end{matrix} \right] A3= ​2120​1220​0111​1121​ ​

A 4 = [ 1 2 1 1 2 2 2 3 3 3 2 3 2 1 0 1 ] A^4=\left[ \begin{matrix} 1&2&1&1\\ 2&2&2&3\\ 3&3&2&3\\ 2&1&0&1\\ \end{matrix} \right] A4= ​1232​2231​1220​1331​ ​

(1)

D中$v_1$到$v_4$长度为4的通路有多少条？

$a_{14}^{(4)}=2$,有两条

(2)

D中$v_1$到$v_1$长度为4的通路有多少条？

$a_{11}^{(3)}=2$，有两条

(3)

D中长度为4通路总数为多少？其中有多少条是回路？

总数为$\stackrel{4}{\sum _{i,j}}{a}_{ij}^{(4)}=29$条通路

其中$\stackrel{4}{\sum _{i,j}}{a}_{ii}^{(4)}=6$条为回路

15

正则图为无向简单图，不可有平行边和环

有2种非同构情况

6和3,3