CNN/RNN python代码和详细解释（学习笔记）

CNN/RNN学习笔记

祎小祎

1. 人工神经网络
神经网络的每个神经元如下

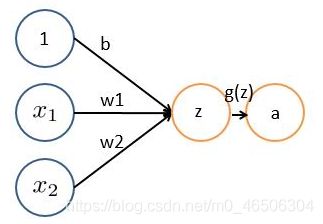
基本wx + b的形式，其中

x1 x2表示输入向量
w为权重，几个输入则意味着有几个权重，即每个输入都被赋予一个权重
b为偏置bias
g(z) 为激活函数
a 为输出

1.1 CNN网络的层级结构
输入层，卷积层，激活层，池化层，全连接FC层。

输入层：对数据做预处理，常见处理方：（1）去均值 （2）归一化 （3）降维

卷积层：人的大脑识别图片的过程中，并不是一下子整张图同时识别，而是对于图片中的每一个特征首先局部感知，然后更高层次对局部进行综合操作，从而得到全局信息。
卷积层使用“卷积核”进行局部感知。举个例子来讲，一个32×32×3的RGB图经过一层5×5×3的卷积后变成了一个28×28×1的特征图，那么输入层共有32×32×3=3072个神经元，第一层隐层会有28×28=784个神经元，这784个神经元对原输入层的神经元只是局部连接。

激励层：对卷积层结果做一次非线性映射。
如果不用激励函数（其实就相当于激励函数是f(x)=x），这种情况下，每一层的输出都是上一层输入的线性函数。容易得出，无论有多少神经网络层，输出都是输入的线性组合，与没有隐层的效果是一样的，这就是最原始的感知机了。

• 使用ReLu时，应调小learning rate,防止出现很多梯度为零的神经元
• 如果不能解决learning rate的问题，就使用Leaky ReLu、PReLu来替代
• 不建议使用sigmoid函数，用tanh替代

池化层：主要用于特征降维，压缩数据和参数的数量，减小过拟合，同时提高模型的容错性。主要有以下两种方式

• Max Pooling：最大池化
• Average Pooling：平均池化

下图展示了一个含有多个卷积层+激励层+池化层的过程：

2.代码

• python 基于keras实现CNN代码 （已经实操可以直接用）
• Keras是一个高层神经网络API，Keras由纯Python编写而成并基Tensorflow、Theano以及CNTK后端。

import numpy as np
#seed( ) 用于指定随机数生成时所用算法开始的整数值。 
np.random.seed(1337)
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution2D, MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
#选取样本数
batch_size = 128
nb_classes = 10
epochs = 5
# input image dimensions
img_rows, img_cols = 28, 28
# 卷积滤波器的数量
nb_filters = 32
# size of pooling area for max pooling
pool_size = (2, 2)
# convolution kernel size 设置卷积核大小
kernel_size = (3, 3)
(X_train, y_train), (X_test, y_test) = mnist.load_data()
from sklearn.model_selection import train_test_split
#x为数据集的feature熟悉，y为label.
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size = 0.2)
 
# 根据不同的backend定下不同的格式
if K.image_dim_ordering() == 'th':
    X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
    X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
    X_valid = X_valid.reshape(X_valid.shape[0], 1, img_rows, img_cols)
    input_shape = (1, img_rows, img_cols)
else:
    X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
    X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
    X_valid = X_valid.reshape(X_valid.shape[0], img_rows, img_cols,1)
    input_shape = (img_rows, img_cols, 1)
 
# 类型转换
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_valid = X_valid.astype('float32')
#数据归一化
X_train /= 255
X_test /= 255
X_valid /= 255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
print(X_valid.shape[0], 'valid samples')
 
# 转换为one_hot类型
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
Y_valid = np_utils.to_categorical(y_valid, nb_classes)
 
#构建模型
model = Sequential()
 
model.add(Convolution2D(nb_filters, (kernel_size[0], kernel_size[1]),
                        padding='same',
                        input_shape=input_shape)) # 卷积层1
model.add(Activation('relu')) #激活层
model.add(Convolution2D(nb_filters, (kernel_size[0], kernel_size[1]))) #卷积层2
model.add(Activation('relu')) #激活层
model.add(MaxPooling2D(pool_size=pool_size)) #池化层
model.add(Dropout(0.25)) #神经元随机失活
model.add(Flatten()) #拉成一维数据
model.add(Dense(128)) #全连接层1
model.add(Activation('relu')) #激活层
model.add(Dropout(0.5)) #随机失活
model.add(Dense(nb_classes)) #全连接层2
model.add(Activation('softmax')) #Softmax评分
 
#编译模型
#设置损失函数为多分类方法，评价指标为：accruracy
#优化器设置为Adagrad，让不同梯度变化的维度有与之适应的学习率
model.compile(loss='categorical_crossentropy',
              optimizer='adadelta',
              metrics=['accuracy'])
#训练模型
model.fit(X_train, Y_train, batch_size=batch_size, epochs=epochs,
          verbose=1, validation_data=(X_valid, Y_valid))
#评估模型
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])

解释：

2.1numpy库：NumPy 是 Python 语言的一个第三方库，其支持大量高维度数组与矩阵运算。此外，NumPy 也针对数组运算提供大量的数学函数。查看numpy库版本的方法：np.version

2.2mnist数据集介绍：minist数据集为手写数据库。分为两部分，分别含有60000张训练图片和10000张测试图片。
2.2.1每一张图片包含28*28个像素：
# input image dimensions img_rows, img_cols = 28, 28
2.2.2使用tensorflow可以直接加载数据集中的数据，但是是按照张量格式加载的，所以无法看清楚图片具体长什么样子。
2.2.3(X_train, y_train), (X_test, y_test) = mnist.load_data() 这行代码加载mnist数据集数据。

2.3.from sklearn.model_selection import train_test_split 导入sklearn库，可以返回切分好的数据集，切分为train和test两个部分。

2.4.X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size = 0.2) 将测试集设置为总数量的0.2。

2.5. K.image_dim_ordering() == ‘th’: 关于通道顺序的设置

2.6. One-hot编码：将类别变量转换为机器学习算法易于利用的一种形式的过程，便于二值化操作。

2.7损失函数，建议初学者看着一个损失函数的内容:
损失函数链接

• RNN python 基于numpy库的代码

（实操可用）

import copy, numpy as np

np.random.seed(0)

# sigmoid函数
def sigmoid(x):
    output = 1 / (1 + np.exp(-x))
    return output

# sigmoid导数
def sigmoid_output_to_derivative(output):
    return output * (1 - output)


# 训练数据生成
int2binary = {}
binary_dim = 8

largest_number = pow(2, binary_dim)
binary = np.unpackbits(
    np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
for i in range(largest_number):
    int2binary[i] = binary[i]

# 初始化一些变量
alpha = 0.1 #学习率
input_dim = 2   #输入的大小
hidden_dim = 8  #隐含层的大小
output_dim = 1  #输出层的大小

# 随机初始化权重
synapse_0 = 2 * np.random.random((hidden_dim, input_dim)) - 1   #(8, 2)
synapse_1 = 2 * np.random.random((output_dim, hidden_dim)) - 1  #(1, 8)
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1  #(8, 8)

synapse_0_update = np.zeros_like(synapse_0) #(8, 2)
synapse_1_update = np.zeros_like(synapse_1) #(1, 8)
synapse_h_update = np.zeros_like(synapse_h) #(8, 8)

# 开始训练
for j in range(100000):

    # 二进制相加
    a_int = np.random.randint(largest_number / 2)  # 随机生成相加的数
    a = int2binary[a_int]  # 映射成二进制值

    b_int = np.random.randint(largest_number / 2)  # 随机生成相加的数
    b = int2binary[b_int]  # 映射成二进制值

    # 真实的答案
    c_int = a_int + b_int   #结果
    c = int2binary[c_int]   #映射成二进制值

    # 待存放预测值
    d = np.zeros_like(c)

    overallError = 0

    layer_2_deltas = list() #输出层的误差
    layer_2_values = list() #第二层的值（输出的结果）
    layer_1_values = list() #第一层的值（隐含状态）
    layer_1_values.append(copy.deepcopy(np.zeros((hidden_dim, 1)))) #第一个隐含状态需要0作为它的上一个隐含状态

    #前向传播
    for i in range(binary_dim):
        X = np.array([[a[binary_dim - i - 1], b[binary_dim - i - 1]]]).T    #(2,1)
        y = np.array([[c[binary_dim - i - 1]]]).T   #(1,1)
        layer_1 = sigmoid(np.dot(synapse_h, layer_1_values[-1]) + np.dot(synapse_0, X)) #(1,1)
        layer_1_values.append(copy.deepcopy(layer_1))   #(8,1)
        layer_2 = sigmoid(np.dot(synapse_1, layer_1))   #(1,1)
        error = -(y-layer_2)    #使用平方差作为损失函数
        layer_delta2 = error * sigmoid_output_to_derivative(layer_2)    #(1,1)
        layer_2_deltas.append(copy.deepcopy(layer_delta2))
        d[binary_dim - i - 1] = np.round(layer_2[0][0])
    future_layer_1_delta = np.zeros((hidden_dim, 1))
    #反向传播
    for i in range(binary_dim):
        X = np.array([[a[i], b[i]]]).T
        prev_layer_1 = layer_1_values[-i-2]
        layer_1 = layer_1_values[-i-1]
        layer_delta2 = layer_2_deltas[-i-1]
        layer_delta1 = np.multiply(np.add(np.dot(synapse_h.T, future_layer_1_delta),np.dot(synapse_1.T, layer_delta2)), sigmoid_output_to_derivative(layer_1))
        synapse_0_update += np.dot(layer_delta1, X.T)
        synapse_h_update += np.dot(layer_delta1, prev_layer_1.T)
        synapse_1_update += np.dot(layer_delta2, layer_1.T)
        future_layer_1_delta = layer_delta1
    synapse_0 -= alpha * synapse_0_update
    synapse_h -= alpha * synapse_h_update
    synapse_1 -= alpha * synapse_1_update
    synapse_0_update *= 0
    synapse_1_update *= 0
    synapse_h_update *= 0
    # 验证结果
    if (j % 100 == 0):
        print("Error:" + str(overallError))
        print("Pred:" + str(d))
        print("True:" + str(c))
        out = 0
        for index, x in enumerate(reversed(d)):
            out += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out))
        print("------------")