Leetcode刷题笔记——剑指offer II (六)【图】
文章目录
- 图
-
- 695. 岛屿的最大面积
- 剑指 Offer II 106. 二分图 (每条边的两个结点都来自不同的集合)
- 剑指 Offer II 107. 矩阵中的距离
- (最短路问题,建图,BFS) 剑指 Offer II 108. 单词演变
- (最短路问题) 剑指 Offer II 109. 开密码锁
- (建图,邻接表,DFS)剑指 Offer II 110. 所有路径
- (建带权有向图,邻接矩阵,DFS) 剑指 Offer II 111. 计算除法
- 剑指 Offer II 112. 最长递增路径
- (拓扑排序:Kahn算法) 剑指 Offer II 113. 课程顺序
- (拓扑排序)剑指 Offer II 114. 外星文字典
- 剑指 Offer II 115. 重建序列
- (并查集) 剑指 Offer II 116. 省份数量
- (并查集) 剑指 Offer II 117. 相似的字符串
- (并查集) 剑指 Offer II 118. 多余的边
- (并查集) 6135. 图中的最长环
- 剑指 Offer II 119. 最长连续序列
- 最小生成树 = (费用排序+并查集)
-
- 1584. 连接所有点的最小费用
- 迪杰斯特拉 单源带权最小路
-
- 1514. 概率最大的路径
图
- 图的搜索:DFS(递归)、BFS(queue)
- 图的表示:邻接表、邻接矩阵、直接用一个list 记录所有的边(最小生成)
- 特殊的数据结构:建立一棵树:并查集 Union Find Set(特殊:二分图)
对于并查集:
分两步:
- 构造函数:
- vector< int> pa; 父节点数组
- int cnt; 连通分量的个数
- vector< int> size; 可选
- 实现两个方法(一般来说,node都不需要自己构造,可用int等结构代替)
- Node find(Node x):返回x的根节点
- void union(Node x, Node y): 将x,y的根节点连在一起
- 优化两个方法
- 确定状态(即有多少个状态需要分类)
然后将所有状态压缩至一个数组中
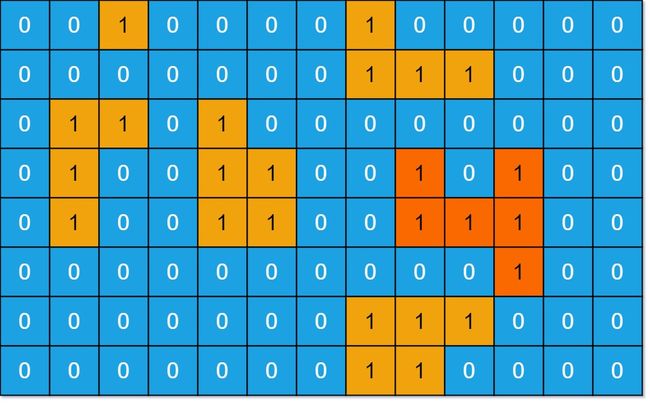
695. 岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1
我的方法:dfs
细节:grid[i][j]=0;将走过的路全部置0;退出后再更新ans,此时的cnt是局部最优值
int cnt=0, ans=0;
int maxAreaOfIsland(vector<vector<int>>& grid) {
for (int i=0; i<grid.size(); ++i){
for (int j=0; j<grid.back().size(); ++j){
dfs(grid, i, j);
ans = max(ans, cnt);//
cnt = 0;
}
}
return ans;
}
void dfs(vector<vector<int>>& grid, int i, int j){
if ((i >= grid.size() || i < 0) || (j >= grid.back().size() || j < 0)) return;
if (grid[i][j]==0) {
return;
}
grid[i][j]=0;//
cnt++;
dfs(grid, i+1, j);
dfs(grid, i, j+1);
dfs(grid, i-1, j);
dfs(grid, i, j-1);
return;
}
方法二:UF集,并查集
[注意点]
// find返回的是根节点(祖先),不是子节点
// union 是将根结点(祖先)连在一起,而不是子节点
// // UF祖先初始化时,进行状态压缩, i ∈ ( 0 , m − 1 ) , j ∈ ( 0 , n − 1 ) i\in (0, m-1), j\in(0,n-1) i∈(0,m−1),j∈(0,n−1), 所以 i i i 应该✖ j j j 的最大值,压缩方程为i*n+j
class Solution {
public:
static constexpr int dirs[4][2] = { {0, 1}, {1, 0}, {-1, 0}, {0, -1} };
bool inArea(vector<vector<int>>& mat, int i, int j) {
return (i >= 0 && i < mat.size()) && j >= 0 && j < mat.back().size();
}
vector<int> paMaxAreaOfIsland; // 父节点
vector<int> sizeMaxAreaOfIsland; // 重量
int maxCnt = 0;
int findUFmaxAreaOfIsland(int x) {// 寻找根节点
while (paMaxAreaOfIsland[x]!=x) {
//路径优化
paMaxAreaOfIsland[x] = paMaxAreaOfIsland[paMaxAreaOfIsland[x]];
x = paMaxAreaOfIsland[x];// 向上寻找父节点
}
return paMaxAreaOfIsland[x];// 返回的根结点!!不是子节点
}
void unionMaxAreaOfIsland(int x, int y) {
// 先判断x, y的根节点是否相同
int xPa = findUFmaxAreaOfIsland(x);
int yPa = findUFmaxAreaOfIsland(y);
if (xPa == yPa) return;
if (sizeMaxAreaOfIsland[xPa] > sizeMaxAreaOfIsland[yPa]) {
paMaxAreaOfIsland[yPa] = xPa;// 是将根节点接上去,而不是子节点!!
sizeMaxAreaOfIsland[xPa] += sizeMaxAreaOfIsland[yPa];
maxCnt = max(sizeMaxAreaOfIsland[xPa], maxCnt);
}
else { // ypa重,则选ypa为根节点
paMaxAreaOfIsland[xPa] = yPa;//
sizeMaxAreaOfIsland[yPa] += sizeMaxAreaOfIsland[xPa];
maxCnt = max(sizeMaxAreaOfIsland[yPa], maxCnt);
}
return;
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
int m = grid.size(), n = grid.back().size();
paMaxAreaOfIsland = vector<int>(m * n);
sizeMaxAreaOfIsland = vector<int>(m * n);
for (int i = 0; i < m; i++) { // UF父节点初始化
for (int j = 0; j < n; j++) {
if (grid[i][j]) {
paMaxAreaOfIsland[n * i + j] = n * i + j;// i*max(j)=i*n (不是i*m)
sizeMaxAreaOfIsland[n * i + j] = 1;
maxCnt = 1;
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (!grid[i][j]) continue;
for (int d = 0; d < 2; ++d) {
int nexti = i + dirs[d][0];
int nextj = j + dirs[d][1];
if (!inArea(grid, nexti, nextj)) continue;
if (grid[nexti][nextj]==1) {
unionMaxAreaOfIsland(i * n + j, nexti * n + nextj);
}
}
}
}
return maxCnt;
}
};
方法三:BFS
bool inArea(vector<vector<int>>& mat, int i, int j) {
return (i >= 0 && i < mat.size()) && j >= 0 && j < mat.back().size();
}
int dirsmaxAreaOfIsland[4][2] = { {-1,0},{0,-1}, {1,0}, {0, 1} };
int maxAreaOfIsland(vector<vector<int>>& grid) {
queue<pair<int, int>> q;
int ans = 0;
vector<vector<bool>> vis(grid.size(), vector<bool>(grid.back().size()));
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid.back().size(); j++) {
if (grid[i][j] == 0 || vis[i][j])continue;
q.emplace(i, j);
vis[i][j] = true;
int tmp = 0;
while (!q.empty()) {
int n = q.size();
for (int k = 0; k < n; ++k) {
auto [curi, curj] = q.front();
q.pop();
tmp++;
for (int d = 0; d < 4; ++d) {
int nexti = curi + dirsmaxAreaOfIsland[d][0];
int nextj = curj + dirsmaxAreaOfIsland[d][1];
if (inArea(grid, nexti, nextj) && grid[nexti][nextj] && !vis[nexti][nextj]) {
q.emplace(nexti, nextj);
vis[nexti][nextj] = true;
}
}
}
}
ans = max(ans, tmp);
}
}
return ans;
}
剑指 Offer II 106. 二分图 (每条边的两个结点都来自不同的集合)
存在一个 无向图 ,图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。
给定一个二维数组 graph ,表示图,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,对于 graph[u] 中的每个 v ,都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性:
不存在自环(graph[u] 不包含 u)。
不存在平行边(graph[u] 不包含重复值)。
如果 v 在 graph[u] 内,那么 u 也应该在 graph[v] 内(该图是无向图)
这个图可能不是连通图,也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义:如果能将一个图的节点集合分割成两个独立的子集 A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合,就将这个图称为 二分图 。
如果图是二分图,返回 true ;否则,返回 false 。
示例 1:
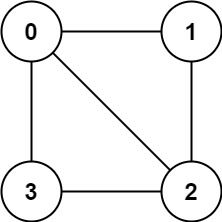
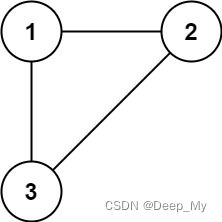
输入:graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出:false
解释:不能将节点分割成两个独立的子集,以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。
示例 2:
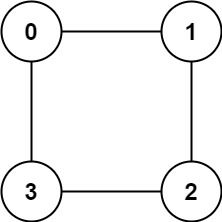
输入:graph = [[1,3],[0,2],[1,3],[0,2]]
输出:true
解释:可以将节点分成两组: {0, 2} 和 {1, 3} 。
提示:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] 不会包含 u
graph[u] 的所有值 互不相同
如果 graph[u] 包含 v,那么 graph[v] 也会包含 u
前言
对于图中的任意两个节点 u u u 和 v v v,如果它们之间有一条边直接相连,那么 u u u 和 v v v 必须属于不同的集合。
如果给定的无向图连通,那么我们就可以任选一个节点开始,给它染成红色。随后我们对整个图进行遍历,将该节点直接相连的所有节点染成绿色,表示这些节点不能与起始节点属于同一个集合。我们再将这些绿色节点直接相连的所有节点染成红色,以此类推,直到无向图中的每个节点均被染色。
如果我们能够成功染色,那么红色和绿色的节点各属于一个集合,这个无向图就是一个二分图;如果我们未能成功染色,即在染色的过程中,某一时刻访问到了一个已经染色的节点,并且它的颜色与我们将要给它染上的颜色不相同,也就说明这个无向图不是一个二分图。
算法的流程如下:
我们任选一个节点开始,将其染成红色,并从该节点开始对整个无向图进行遍历;
在遍历的过程中,如果我们通过节点 u u u 遍历到了节点 v v v(即 u u u 和 v v v 在图中有一条边直接相连),那么会有两种情况:
如果 v v v 未被染色,那么我们将其染成与 u u u 不同的颜色,并对 v v v 直接相连的节点进行遍历;
如果 v v v 被染色,并且颜色与 u u u 相同,那么说明给定的无向图不是二分图。我们可以直接退出遍历并返回 false \text{false} false 作为答案。
当遍历结束时,说明给定的无向图是二分图,返回 true \text{true} true 作为答案。
我们可以使用「深度优先搜索」或「广度优先搜索」对无向图进行遍历,下文分别给出了这两种搜索对应的代码。
注意:题目中给定的无向图不一定保证连通,因此我们需要进行多次遍历,直到每一个节点都被染色,或确定答案为 false \text{false} false 为止。每次遍历开始时,我们任选一个未被染色的节点,将所有与该节点直接或间接相连的节点进行染色。
方法一:深度优先搜索
static constexpr int UNCOLORED = 0;
static constexpr int RED = 1;
static constexpr int GREEN = 2;
vector<int> color;
bool valid;
void dfs(int node, int c, const vector<vector<int>>& graph) {
color[node] = c;
int cNei = (c == RED ? GREEN : RED);
for (int neighbor: graph[node]) {
if (color[neighbor] == UNCOLORED) {
dfs(neighbor, cNei, graph);
if (!valid) {
return;
}
}
else if (color[neighbor] != cNei) {
valid = false;
return;
}
}
}
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
valid = true;
color.assign(n, UNCOLORED);
for (int i = 0; i < n && valid; ++i) {
if (color[i] == UNCOLORED) {
dfs(i, RED, graph);
}
}
return valid;
}
方法二:BFS
// constexpr 静态数据成员声明需要类内初始值设定项
static constexpr int UNCLORED = 0;
static constexpr int RED = 1;
static constexpr int GREEN = 2;
vector<int> color;
bool valid;
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
color.assign(n, UNCLORED);
for (int i = 0; i < n; ++i) { //对每个结点都遍历一次
if (color[i] == UNCLORED) {// 如果该结点未被赋值,则记为red
queue<int> q;
q.push(i);
color[i] = RED;
while (!q.empty()) {
int nQ = q.size();
for (int i = 0; i < nQ; ++i) {
int curNode = q.front(); q.pop();
int c = color[curNode];
int c2 = (c == RED ? GREEN : RED);
for (int neighbor : graph[curNode]) {
if (color[neighbor] == UNCLORED) {
color[neighbor] = c2; // 该邻结点记为c2(c的反面)
q.push(neighbor);
}
else {
if (color[neighbor] == c) {
return false;
}
}
}
}
}
}
}
return true;
}
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
color = [0]*len(graph)
from queue import Queue
q = Queue()
for j in range(len(graph)):
if color[j]!=0: continue
q.put((j, graph[j]))
color[j] = 1
while not q.empty():
n = q.qsize()
for i in range(n):
idx, nodeCur = q.get()
for it in nodeCur:
if color[it]==0:
q.put((it, graph[it]))
color[it] = -color[idx]
elif color[it] == -color[idx]:
continue
else:
return False
return True
方法三:并查集
- 根据题意,对于每个节点来说,与它相连通的所有节点都应该加入同一个集合中,但是该节点不能与它们在同一个集合中。
- 如果中途发现某个节点和它联通的节点处于同一个集合中了,那么无法二分
UF u(2*n);
u.unionMyUF(i, child + n);
u.unionMyUF(i + n, child);
i 与 j + n 相连 => i, j位于二分图两端,因为我们的循环范围只是从0到n-1。
class UF {
private:
int cnt; // 连通分量的个数
vector<int> pa; // 存储一棵树
vector<int> size; // 记录数的重量
public:
UF(int n) { //
this->cnt = n;
pa = vector<int>(n);
size = vector<int>(n);
for (int i = 0; i < n; ++i) {
pa[i] = i;
size[i] = 1;
}
}
int find(int x) { //
while (pa[x] != x) {
// 进行路径压缩
pa[x] = pa[pa[x]];
x = pa[x];
}
return x;
}
void unionMyUF(int p, int q) { //
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// 小接到大下面,较平衡
if (size[rootP] > size[rootQ]) {
pa[rootQ] = rootP;
size[rootP] += size[rootQ];
}
else {
pa[rootP] = rootQ;
size[rootQ] += size[rootP];
}
cnt--;
}
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int count() { return cnt; }
};
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
UF u(2*n); // i 与 j + n 相连 => i, j位于二分图两端
for (int i = 0; i < n; ++i) {
for (int child : graph[i]) {
if (u.connected(i, child)) return false;
u.unionMyUF(i, child + n);
u.unionMyUF(i + n, child);
}
}
return true;
}
我的并查集
- 构造函数:
pa = [i for i in range(len(graph))], 我只设置了 len(graph) 个状态cnt = len(graph),初始 n 个连通分量size = [1]*n, 每个节点的size设置为1
- 方法:(略,未优化)【主要是 的那几个方法】
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
pa = [i for i in range(len(graph))]
size = [1]*len(graph)
def find(x:int)->int:
while pa[x]!=x:
pa[x] = pa[pa[x]]
x = pa[x]
return x
def union(x:int, y:int)->None:
xP = find(x)
yP = find(y)
pa[xP] = yP
size [yP] += size[xP]
for i in range(len(graph)):
pre = None
for it in graph[i]:
if pa[i]==pa[it]:
return False
elif pre!=None:
union(pre, it)
pre = it
return True
剑指 Offer II 107. 矩阵中的距离
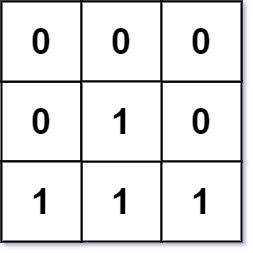
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0
我的解法:BFS
注意要点:
1、找准起始点,我们这里从0开始进入bfs,则矩阵中所有的0都将同时开始进入BFS队列
```cpp
static constexpr int dirs[4][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
bool inArea(vector<vector<int>>& mat, int i, int j) {
return (i >= 0 && i < mat.size()) && j >= 0 && j < mat.back().size();
}
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
vector<vector<int>> ans(mat.size(), vector<int>(mat.back().size(), INT_MAX));
vector<vector<bool>> vis(mat.size(), vector<bool>(mat.back().size(), true));
queue<pair<int, int>> q;
for (int i = 0; i < mat.size(); ++i) { //找到所有0作为bfs的起点,放入队列
for (int j = 0; j < mat.back().size(); ++j) {
if (mat[i][j] != 0) continue;
ans[i][j] = 0;
vis[i][j] = false;
q.push(pair<int, int> (i, j));
}
}
int step = 0, curI, curJ;
while (!q.empty()) {
int repeat = q.size();
for (int i = 0; i < repeat; ++i) {
auto [curI, curJ] = q.front(); // c++17 结构化绑定
q.pop();
vis[curI][curJ] = false;
ans[curI][curJ] = min(ans[curI][curJ], step); // 所有0到该点的最短距离
for (int d = 0; d < 4; ++d) {
int nextI = curI + dirs[d][0], nextJ = curJ + dirs[d][1];
if (inArea(mat, nextI, nextJ) && vis[nextI][nextJ]) {
q.push(pair<int, int>(nextI, nextJ));
}
}
}
step++;
}
return ans;
}
方法:BFS
对于矩阵中的每一个元素,如果它的值为 0,那么离它最近的 0 就是它自己。如果它的值为 1,那么我们就需要找出离它最近的 0,并且返回这个距离值。那么我们如何对于矩阵中的每一个 1,都快速地找到离它最近的 0 呢?
我们不妨从一个简化版本的问题开始考虑起。假设这个矩阵中恰好只有一个 0,我们应该怎么做?由于矩阵中只有一个 0,那么对于每一个 1,离它最近的 0 就是那个唯一的 0。如何求出这个距离呢?我们可以想到两种做法:
如果 0 在矩阵中的位置是 ( i 0 , j 0 ) (i_0, j_0) (i0,j0), 1 在矩阵中的位置是 ( i 1 , j 1 ) (i_1, j_1) (i1,j1),那么我们可以直接算出 0 和 1 之间的距离。因为我们从 1 到 0 需要在水平方向走 ∣ i 0 − i 1 ∣ |i_0 - i_1| ∣i0−i1∣步,竖直方向走 ∣ j 0 − j 1 ∣ |j_0 - j_1| ∣j0−j1∣步,那么它们之间的距离就为 ∣ i 0 − i 1 ∣ + ∣ j 0 − j 1 ∣ |i_0 - i_1| + |j_0 - j_1| ∣i0−i1∣+∣j0−j1∣
我们可以从 00 的位置开始进行 广度优先搜索。广度优先搜索可以找到从起点到其余所有点的 最短距离,因此如果我们从 00 开始搜索,每次搜索到一个 11,就可以得到 00 到这个 11 的最短距离,也就离这个 11 最近的 00 的距离了(因为矩阵中只有一个 00)。
举个例子,如果我们的矩阵为:
_ _ _ _
_ 0 _ _
_ _ _ _
_ _ _ _
其中只有一个 00,剩余的 11 我们用短横线表示。如果我们从 00 开始进行广度优先搜索,那么结果依次为:
_ _ _ _ _ 1 _ _ 2 1 2 _ 2 1 2 3 2 1 2 3
_ 0 _ _ ==> 1 0 1 _ ==> 1 0 1 2 ==> 1 0 1 2 ==> 1 0 1 2
_ _ _ _ _ 1 _ _ 2 1 2 _ 2 1 2 3 2 1 2 3
_ _ _ _ _ _ _ _ _ 2 _ _ 3 2 3 _ 3 2 3 4
也就是说,在广度优先搜索的每一步中,如果我们从矩阵中的位置 x 搜索到了位置 y,并且 y 还没有被搜索过,那么位置 y 离 0 的距离就等于位置 x 离 0 的距离加上 1。
对于上面的两种做法,第一种看上去简洁有效,只需要对每一个位置计算就行;第二种需要实现广度优先搜索,会复杂一些。但是,别忘了我们的题目中会有不止一个 0,这样以来,如果我们要使用第一种做法,就必须对于每个 1 计算一次它到所有的 0 的距离,再从中取一个最小值,时间复杂度会非常高,无法通过本地。而对于第二种做法,我们可以很有效地处理有多个 0 的情况。
事实上,第一种做法也是可以处理多个 0 的情况的,但没有那么直观。感兴趣的读者可以在理解完方法一(即本方法)之后阅读方法二,那里介绍了第一种做法是如何扩展的。
处理的方法很简单:我们在进行广度优先搜索的时候会使用到队列,在只有一个 0 的时候,我们在搜索前会把这个 0 的位置加入队列,才能开始进行搜索;如果有多个 0,我们只需要把这些 0 的位置都加入队列就行了。
我们还是举一个例子,在这个例子中,有两个 0:
_ _ _ _
_ 0 _ _
_ _ 0 _
_ _ _ _
我们会把这两个 0 的位置都加入初始队列中,随后我们进行广度优先搜索,找到所有距离为 1 的 1:
_ 1 _ _
1 0 1 _
_ 1 0 1
_ _ 1 _
接着重复步骤,直到搜索完成:
_ 1 _ _ 2 1 2 _ 2 1 2 3
1 0 1 _ ==> 1 0 1 2 ==> 1 0 1 2
_ 1 0 1 2 1 0 1 2 1 0 1
_ _ 1 _ _ 2 1 2 3 2 1 2
这样做为什么是正确的呢?
我们需要对于每一个 1 找到离它最近的 0。如果只有一个 0 的话,我们从这个 0 开始广度优先搜索就可以完成任务了;
但在实际的题目中,我们会有不止一个 0。我们会想,要是我们可以把这些 0 看成一个整体好了。有了这样的想法,我们可以添加一个「超级零」,它与矩阵中所有的 0 相连,这样的话,任意一个 1 到它最近的 0 的距离,会等于这个 1 到「超级零」的距离减去一。由于我们只有一个「超级零」,我们就以它为起点进行广度优先搜索。这个「超级零」只和矩阵中的 0 相连,所以在广度优先搜索的第一步中,「超级零」会被弹出队列,而所有的 0 会被加入队列,它们到「超级零」的距离为 1。这就等价于:一开始我们就将所有的 0 加入队列,它们的初始距离为 0。这样以来,在广度优先搜索的过程中,我们每遇到一个 1,就得到了它到「超级零」的距离减去一,也就是 这个 1 到最近的 0 的距离。
private:
static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> dist(m, vector<int>(n));
vector<vector<int>> seen(m, vector<int>(n));
queue<pair<int, int>> q;
// 将所有的 0 添加进初始队列中
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 0) {
q.emplace(i, j);
seen[i][j] = 1;
}
}
}
// 广度优先搜索
while (!q.empty()) {
auto [i, j] = q.front();
q.pop();
for (int d = 0; d < 4; ++d) {
int ni = i + dirs[d][0];
int nj = j + dirs[d][1];
if (ni >= 0 && ni < m && nj >= 0 && nj < n && !seen[ni][nj]) {
dist[ni][nj] = dist[i][j] + 1;
q.emplace(ni, nj);
seen[ni][nj] = 1;
}
}
}
return dist;
}
(最短路问题,建图,BFS) 剑指 Offer II 108. 单词演变
在字典(单词列表) wordList 中,从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
序列中第一个单词是 beginWord 。
序列中最后一个单词是 endWord 。
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典 wordList 中的单词。
给定两个长度相同但内容不同的单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同
我的方法:BFS, 超时
将每个单词看作一个节点,单词之间若相差一个字符,则创建边,从而构建一幅图
通过BFS,找到起点到终点的最短路
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
if endWord not in wordList:
return 0
idx_end = wordList.index(endWord) + 1
graphNode = [beginWord]
graphNode.extend(wordList)
n = len(graphNode)
edge = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(i):
cnt = 0
for k in range(len(graphNode[i])):
if cnt>1: break
if graphNode[i][k]!=graphNode[j][k]:
cnt += 1
if cnt==1:
edge[i][j] = 1
edge[j][i] = 1
from queue import Queue
q = Queue()
q.put((0, edge[0]))
step = 0
while not q.empty():
size = q.qsize()
step += 1
for _ in range(size):
idx, cur = q.get()
if idx==idx_end:
return step
for i in range(n):
if cur[i]==0 or graphNode[i] == "0": continue
graphNode[i] = "0"
q.put((i, edge[i]))
return 0
超时原因,图的结点太多,BFS非常耗时
优化建图
具体地,我们可以创建虚拟节点。对于单词 hit,我们创建三个虚拟节点 *it、h*t、hi*,并让 hit 向这三个虚拟节点分别连一条边即可。如果一个单词能够转化为 hit,那么该单词必然会连接到这三个虚拟节点之一。对于每一个单词,我们枚举它连接到的虚拟节点,把该单词对应的 id 与这些虚拟节点对应的 id 相连即可。
最后我们将起点加入队列开始广度优先搜索,当搜索到终点时,我们就找到了最短路径的长度。注意因为添加了虚拟节点,所以我们得到的距离为实际最短路径长度的两倍。同时我们并未计算起点对答案的贡献,所以我们应当返回距离的一半再加一的结果
void LLaddWord(string& word,
unordered_map<string, int>& wordId,
vector<vector<int>>& edge, int& nodeNum){
// 检查字典中是否有word,如果没有,则加入新的id(按加入顺序增大)
if (!wordId.count(word)){
wordId[word] = nodeNum++;
edge.emplace_back();
}
}
void LLaddEdge(string& word,
unordered_map<string, int>& wordId,
vector<vector<int>>& edge, int& nodeNum){
LLaddWord(word, wordId, edge, nodeNum);
int id1 = wordId[word];
for (char& it: word){
char tmp = it;
it = '*'; // 改其中一个字符
LLaddWord(word, wordId, edge, nodeNum);
int id2 = wordId[word];
edge[id1].push_back(id2);
edge[id2].push_back(id1);
it = tmp;
}
}
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_map<string, int> wordID;
vector<vector<int>> edge;
int nodeNum = 0; // 单词顺序索引
for (auto& word: wordList){
LLaddEdge(word, wordID, edge, nodeNum);
}
LLaddEdge(beginWord, wordID, edge, nodeNum);
if (!wordID.count(endWord)) return 0;
vector<int> dis(nodeNum, INT_MAX); // 记录每个单词的距离
int beginID = wordID[beginWord], endID = wordID[endWord];
dis[beginID] = 0;
queue<int> q;
q.push(beginID);
while(!q.empty()){
int x = q.front(); q.pop();
if (x==endID){
return dis[endID] / 2 + 1;
}
for (int& it : edge[x]){
if (dis[it]==INT_MAX){
dis[it] = dis[x] + 1;
q.push(it);
}
}
}
return 0;
}
(最短路问题) 剑指 Offer II 109. 开密码锁
一个密码锁由 4 个环形拨轮组成,每个拨轮都有 10 个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转:例如把 ‘9’ 变为 ‘0’,‘0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000’ ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,请给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,因为当拨动到 "0102" 时这个锁就会被锁定。
示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:
把最后一位反向旋转一次即可 "0000" -> "0009"。
示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:
无法旋转到目标数字且不被锁定。
示例 4:
输入: deadends = ["0000"], target = "8888"
输出:-1
提示:
1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target 不在 deadends 之中
target 和 deadends[i] 仅由若干位数字组成
我的方法,BFS
每个节点都与 8 个节点相连,即
4位数,每位数 +1 或 -1 所形成的节点,共8个
每次加完,都将其放入 deadSet中,作为备忘录
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
if target=="0000": return 0
deadSet = set(deadends)
if "0000" in deadSet: return -1
def helper(s: List[str], idx: int)->list:
tmp = s[:] # 等价于 s.copy(), copy.copy(s)
sInt = int(tmp[idx])
tmp[idx] = str(sInt+1) if sInt!=9 else "0"
return tmp
def helperMinu(s: List[str], idx: int)->list:
tmp = s[:] # 等价于 s.copy(), copy.copy(s)
sInt = int(tmp[idx])
tmp[idx] = str(sInt-1) if sInt!=0 else "9"
return tmp
q = deque()
q.append("0000")
ans = -1
deadSet.add("0000")
while q.__len__()!=0:
size = len(q)
ans += 1
for _ in range(size):
cur = q.popleft()
if cur==target:
return ans
tarList = list(cur)
for d in range(4):
tmp = helper(tarList, d)
tmpStr = "".join(tmp)
if tmpStr not in deadSet:
deadSet.add(tmpStr)
q.append(tmpStr)
tmp = helperMinu(tarList, d)
tmpStr = "".join(tmp)
if tmpStr not in deadSet:
deadSet.add(tmpStr)
q.append(tmpStr)
return -1
官解:BFS,使用yield生成器
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
if target == "0000":
return 0
dead = set(deadends)
if "0000" in dead:
return -1
def num_prev(x: str) -> str:
return "9" if x == "0" else str(int(x) - 1)
def num_succ(x: str) -> str:
return "0" if x == "9" else str(int(x) + 1)
# 枚举 status 通过一次旋转得到的数字
def get(status: str) -> Generator[str, None, None]:
s = list(status)
for i in range(4):
num = s[i]
s[i] = num_prev(num)
yield "".join(s)
s[i] = num_succ(num)
yield "".join(s)
s[i] = num
q = deque([("0000", 0)])
seen = {"0000"}
while q:
status, step = q.popleft()
for next_status in get(status):
if next_status not in seen and next_status not in dead:
if next_status == target:
return step + 1
q.append((next_status, step + 1))
seen.add(next_status)
return -1
(建图,邻接表,DFS)剑指 Offer II 110. 所有路径
给定一个有 n 个节点的有向无环图,用二维数组 graph 表示,请找到所有从 0 到 n-1 的路径并输出(不要求按顺序)。
graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a ),若为空,就是没有下一个节点了。
示例 1:
输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
示例 3:
输入:graph = [[1],[]]
输出:[[0,1]]
示例 4:
输入:graph = [[1,2,3],[2],[3],[]]
输出:[[0,1,2,3],[0,2,3],[0,3]]
示例 5:
输入:graph = [[1,3],[2],[3],[]]
输出:[[0,1,2,3],[0,3]]
提示:
n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i
保证输入为有向无环图 (GAD)
class Solution:
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
def dfs(graph: List[List[int]],
node: int,
ans: List[List[int]],
tmp: List[int]):
if node==len(graph)-1:
ans.append(tmp.copy())
return
for i in graph[node]:
tmp.append(i)
dfs(graph, i, ans, tmp)
tmp.pop()
ans =[]
dfs(graph, 0, ans, [0])
return ans
(建带权有向图,邻接矩阵,DFS) 剑指 Offer II 111. 计算除法
给定一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意:输入总是有效的。可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]
提示:
1 <= equations.length <= 20
equations[i].length == 2
1 <= Ai.length, Bi.length <= 5
values.length == equations.length
0.0 < values[i] <= 20.0
1 <= queries.length <= 20
queries[i].length == 2
1 <= Cj.length, Dj.length <= 5
Ai, Bi, Cj, Dj 由小写英文字母与数字组成
我的方法:DFS
以equations出现的字符作为节点,values作为有向边的权重
使用dfs计算queries(节点1 到 节点2的权重乘积)的结果
def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
graphSet = set([it for lst in equations for it in lst])
graphMap = dict()
## 节点编号
for i, it in enumerate(graphSet):
graphMap[it] = i
nodeNums = len(graphSet)
edge = [[0.]*nodeNums for _ in range(nodeNums)]
## 边的权重
for idx, lst in enumerate(equations):
i, j = graphMap[lst[0]], graphMap[lst[1]]
edge[i][j] = values[idx]
edge[j][i] = 1/values[idx]
for i in range(nodeNums):
edge[i][i] = 1.0
def dfs(edge: List[List[float]], node:int, end: int, ans: List[float], idx: int, mlt: float, vis: Set[int]):
if node==end:
ans[idx] = mlt
return
for j, weight in enumerate(edge[node]):
if weight==0 or j in vis: continue
if ans[idx] != -1.0: break
vis.add(j)
dfs(edge, j, end, ans, idx, mlt*weight, vis)
return
ans = [-1.0]*queries.__len__()
for idx, lst in enumerate(queries):
if lst[0] not in graphSet or lst[1] not in graphSet: continue
start, end = graphMap[lst[0]], graphMap[lst[1]]
vis = {start}
dfs(edge, start, end, ans, idx, 1.0, vis)
return ans
剑指 Offer II 112. 最长递增路径
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
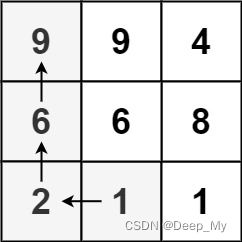
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]]
输出:1
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1
我的方法:dfs
class Solution:
def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
m, n = len(matrix), len(matrix[-1])
vis = [[0]*n for _ in range(m)]
dir = [[1, 0], [-1, 0], [0, 1], [0, -1]]
def inArea(mat: List[List[int]], i:int, j:int):
return 0<=i<len(mat) and 0<=j<len(mat[-1])
self.ans = 1
def dfs(matrix: List[List[int]], dir: List[List[int]],
vis: List[List[int]], i:int, j:int, pre: int):
if matrix[i][j]<=pre:
return 0
elif vis[i][j]!=0:
return vis[i][j]
else:
for di, dj in dir:
if not inArea(matrix, i+di, j+dj): continue
vis[i][j] = max(vis[i][j],
dfs(matrix, dir, vis, i+di, j+dj, matrix[i][j]) + 1)
self.ans = max(self.ans, vis[i][j])
return vis[i][j]
for i in range(m):
for j in range(n):
dfs(matrix, dir, vis, i, j, -float("inf"))
return self.ans
(拓扑排序:Kahn算法) 剑指 Offer II 113. 课程顺序
现在总共有 numCourses 门课需要选,记为 0 到 numCourses-1。
给定一个数组 prerequisites ,它的每一个元素 prerequisites[i] 表示两门课程之间的先修顺序。 例如 prerequisites[i] = [ai, bi] 表示想要学习课程 ai ,需要先完成课程 bi 。
请根据给出的总课程数 numCourses 和表示先修顺序的 prerequisites 得出一个可行的修课序列。
可能会有多个正确的顺序,只要任意返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入: numCourses = 2, prerequisites = [[1,0]]
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3:
输入: numCourses = 1, prerequisites = []
输出: [0]
解释: 总共 1 门课,直接修第一门课就可。
提示:
1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
prerequisites 中不存在重复元素
本题不能简单的使用BFS,因为涉及到排序问题
预习
本题是一道经典的「 拓扑排序 \color{red}拓扑排序 拓扑排序」问题。
给定一个包含 n n n 个节点的 有向图 \color{magenta}有向图 有向图 G G G,我们给出它的节点编号的一种排列,如果满足:
- 对于图 G G G 中的任意一条有向边 ( u , v ) (u,v) (u,v), u u u 在排列中都出现在 v v v 的前面。
那么称该排列是图 G G G 的「 拓扑排序 \color{red}拓扑排序 拓扑排序」。根据上述的定义,我们可以得出两个结论:
-
如果图 G G G 中 存在环 \color{magenta}存在环 存在环(即图 G G G 不是「有向无环图」),那么图 G G G 不存在拓扑排序。这是因为假设图中存在环 x 1 , x 2 , ⋯ , x n , x 1 x_1, x_2, \cdots, x_n, x_1 x1,x2,⋯,xn,x1 ,那么 x 1 x_1 x1 在排列中必须出现在 x n x_n xn 的前面,但 x n x_n xn 同时也必须出现在 x 1 x_1 x1 的前面,因此不存在一个满足要求的排列,也就不存在拓扑排序;
-
如果图 G G G 是 有向无环图 \color{magenta}有向无环图 有向无环图,那么它的拓扑排序可能不止一种。举一个最极端的例子,如果图 G G G 值包含 n n n 个节点却没有任何边,那么任意一种编号的排列都可以作为 拓扑排序 \color{red}拓扑排序 拓扑排序。
有了上述的简单分析,我们就可以将本题建模成一个求拓扑排序的问题了:
-
我们将每一门课看成一个节点;
-
如果想要学习课程 A A A 之前必须完成课程 B B B,那么我们从 B B B 到 A A A 连接一条有向边。这样以来,在拓扑排序中, B B B 一定出现在 A A A 的前面。
在拓扑排序中有两个重要概念,即 出度 \color{red}\text{\colorbox{yellow}{出度}} 出度 和 入度 \color{red}\text{\colorbox{yellow}{入度}} 入度。
- 节点的入度是指以该节点为终点的边的数目,
- 而节点的出度是指以该节点为起点的边的数目。
一种 常用的拓扑排序算法:Kahn 是
- 每次都从有向无环图中取出 入度为 0 的节点 添加到拓扑排序的序列中 \color{red}添加到拓扑排序的序列中 添加到拓扑排序的序列中,然后 删除以该节点为起点的边。
- 重复以上过程,直至图为空或者不存在入度为 0 的节点,
- 若最终图为空,那么图就是一个有向无环图,
- 若最终图不为空且已不存在入度为 0 的节点,那么该图一定有环。
方法:广度优先搜索
思路
方法一的深度优先搜索是一种「逆向思维」:最先被放入栈中的节点是在拓扑排序中最后面的节点。我们也可以使用 正向思维,顺序地生成拓扑排序,这种方法也更加直观。
我们考虑拓扑排序中最前面的节点,该节点一定不会有任何入边,也就是它没有任何的先修课程要求。当我们将一个节点加入答案中后,我们就可以移除它的所有出边,代表着它的相邻节点少了一门先修课程的要求。如果某个相邻节点变成了「没有任何入边的节点」,那么就代表着这门课可以开始学习了。按照这样的流程,我们不断地将没有入边的节点加入答案,直到答案中包含所有的节点(得到了一种拓扑排序)或者不存在没有入边的节点(图中包含环)。
上面的想法类似于广度优先搜索,因此我们可以将广度优先搜索的流程与拓扑排序的求解联系起来。
算法
我们使用一个队列来进行广度优先搜索。开始时,所有 入度为 0 0 0(即流入节点为0) 的节点都被放入队列中,它们就是可以作为拓扑排序最前面的节点,并且它们之间的相对顺序是无关紧要的。
在广度优先搜索的每一步中,我们取出队首的节点 u u u:
-
我们将 u u u 放入答案中;
-
我们移除 u u u 的所有出边,也就是将 u u u 的所有相邻节点的入度减少 1 1 1。如果某个相邻节点 v v v 的入度变为 0 0 0,那么我们就将 v v v 放入队列中。
在广度优先搜索的过程结束后。如果答案中包含了这 n n n 个节点,那么我们就找到了一种拓扑排序,否则说明图中存在环,也就不存在拓扑排序了。
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> edge(numCourses, vector<int>());
vector<int> indeg(numCourses, 0);
for (const auto& it: prerequisites){
int start=it[0], end = it[1];
edge[end].push_back(start);
indeg[start]++;
}
queue<int> q;
for (int i=0; i<numCourses; i++){
if (indeg[i]==0) q.push(i);
}
vector<int> ans;
while (!q.empty())
{
int cur = q.front();
q.pop();
if (indeg[cur]==0) ans.push_back(cur);
for (auto& nxt : edge[cur]){
indeg[nxt]--;
if (indeg[nxt]==0) q.push(nxt);
}
}
if (ans.size()==numCourses) return ans;
return {};
}
class Solution:
def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
edges = defaultdict(list)
indeg = [0]*numCourses # 记录节点的入度值
result = list()
for info in prerequisites:
edges[info[1]].append(info[0])
indeg[info[0]] += 1
import queue
q = queue.Queue()
for u in range(numCourses):
if indeg[u]==0:
q.put(u)
while not q.empty():
cur = q.get()
result.append(cur)
for v in edges[cur]:
indeg[v] -= 1
if indeg[v]==0:
q.put(v)
if len(result)!=numCourses:
result = list()
return result
复杂度分析
-
时间复杂度: O ( n + m ) O(n+m) O(n+m),其中 n n n 为课程数, m m m 为先修课程的要求数。这其实就是对图进行广度优先搜索的时间复杂度。
-
空间复杂度: O ( n + m ) O(n+m) O(n+m)。题目中是以列表形式给出的先修课程关系,为了对图进行广度优先搜索,我们需要存储成邻接表的形式,空间复杂度为 O ( n + m ) O(n+m) O(n+m)。在广度优先搜索的过程中,我们需要最多 O ( n ) O(n) O(n) 的队列空间(迭代)进行广度优先搜索,并且还需要若干个 O ( n ) O(n) O(n) 的空间存储节点入度、最终答案等。
(拓扑排序)剑指 Offer II 114. 外星文字典
现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。
给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。
请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序 排列。若不存在合法字母顺序,返回 “” 。若存在多种可能的合法字母顺序,返回其中 任意一种 顺序即可。
字符串 s 字典顺序小于 字符串 t 有两种情况:
在第一个不同字母处,如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前,那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同,那么 s.length < t.length 时,s 的字典顺序也小于 t 。
示例 1:
输入:words = ["wrt","wrf","er","ett","rftt"]
输出:"wertf"
示例 2:
输入:words = ["z","x"]
输出:"zx"
示例 3:
输入:words = ["z","x","z"]
输出:""
解释:不存在合法字母顺序,因此返回 "" 。
提示:
1 <= words.length <= 100
1 <= words[i].length <= 100
words[i] 仅由小写英文字母组成
前言
这道题是 拓扑排序 \color{red}拓扑排序 拓扑排序 问题。外星文字典中的 字母 和 字母顺序 可以看成 有向图,字典顺序即为所有字母的一种排列,满足每一条有向边的起点字母和终点字母的顺序都和这两个字母在排列中的顺序相同,该排列即为有向图的拓扑排序。
只有当 有向图中无环 \color{red}有向图中无环 有向图中无环 时,才有 拓扑排序 \color{red}拓扑排序 拓扑排序 ,且拓扑排序可能不止一种。如果有向图中有环,则环内的字母不存在符合要求的排列,因此没有拓扑排序。
使用拓扑排序求解时,将外星文字典中的每个字母看成一个节点,将字母之间的顺序关系看成有向边。对于外星文字典中的两个相邻单词,同时从左到右遍历,当遇到第一个不相同的字母时,该位置的两个字母之间即存在顺序关系。
以下两种情况 不存在 合法字母顺序:
-
字母之间的顺序关系存在由至少 22 个字母组成的 环,例如 words = [ “a" , “b" , “a" ] \textit{words} = [\text{``a"}, \text{``b"}, \text{``a"}] words=[“a",“b",“a"];
-
相邻两个单词满足后面的单词是前面的单词的前缀,且后面的单词的长度小于前面的单词的长度,例如 words = [ “ab" , “a" ] \textit{words} = [\text{``ab"}, \text{``a"}] words=[“ab",“a"]。
其余情况下都存在合法字母顺序,可以使用拓扑排序得到字典顺序。
拓扑排序可以使用深度优先搜索或广度优先搜索实现,以下分别介绍两种实现方法。
方法一:拓扑排序 + 深度优先搜索
使用深度优先搜索实现拓扑排序的总体思想是:对于一个特定节点,如果该节点的所有相邻节点都已经搜索完成,则该节点也会变成已经搜索完成的节点,在拓扑排序中,该节点位于其所有相邻节点的前面。一个节点的相邻节点指的是从该节点出发通过一条有向边可以到达的节点。
由于拓扑排序的顺序和搜索完成的 顺序相反,因此需要使用一个栈存储所有已经搜索完成的节点。深度优先搜索的过程中需要维护每个节点的状态,每个节点的状态可能有三种情况:「未访问」、「访问中」和「已访问」。初始时,所有节点的状态都是「未访问」。
每一轮搜索时,任意选取一个「未访问」的节点 u u u,从节点 u u u 开始深度优先搜索。将节点 u u u 的状态更新为「访问中」,对于每个与节点 u u u 相邻的节点 v v v,判断节点 v v v 的状态,执行如下操作:
- 如果节点 v v v 的状态是「未访问」,则继续搜索节点 v v v;
- 如果节点 v v v 的状态是「访问中」,则找到有向图中的环,因此不存在拓扑排序;
- 如果节点 v v v 的状态是「已访问」,则节点 v v v 已经搜索完成并入栈,节点 u u u 尚未入栈,因此节点 u u u 的拓扑顺序一定在节点 v v v 的前面,不需要执行任何操作。
- 当节点 u u u 的所有相邻节点的状态都是「已访问」时,将节点 u u u 的状态更新为「已访问」,并将节点 u u u 入栈。
当所有节点都访问结束之后,如果没有找到有向图中的环,则存在拓扑排序,所有节点从栈顶到栈底的顺序即为拓扑排序。
实现方面,由于每个节点是一个字母,因此可以使用字符数组代替栈,当节点入栈时,在字符数组中按照从后往前的顺序依次填入每个字母。当所有节点都访问结束之后,将字符数组转成字符串,即为字典顺序。
class Solution:
def alienOrder(self, words: List[str])->str:
g = {}
for c in words[0]:
g[c] = []
for s, t in itertools.pairwise(words):
for c in t:
g.setdefault(c, [])
for u, v in zip(s, t):
if u!=v:
g[u].append(v)
break
else: #表示循环执行完了,并且没有执行break
if len(s)>len(t):
return ""
ONGOING, END = 1, 2
states = {}
order = []
def dfs(u: str)->bool:
states[u] = ONGOING
for v in g[u]: # 对于 u 的每一条边的节点
if v not in states: # 如果 v 未被访问
if not dfs(v): # dfs
return False
elif states[v] == ONGOING: # 如果 v 曾被访问,则存在环
return False
order.append(u)
states[u] = END
return True
return "".join(reversed(order)) if all(dfs(u) for u in g if u not in states) else ""
剑指 Offer II 115. 重建序列
给定一个长度为 n 的整数数组 nums ,其中 nums 是范围为 [1,n] 的整数的排列。还提供了一个 2D 整数数组 sequences ,其中 sequences[i] 是 nums 的子序列。
检查 nums 是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列,并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences ,可能存在多个有效的 超序列 。
例如,对于 sequences = [[1,2],[1,3]] ,有两个最短的 超序列 ,[1,2,3] 和 [1,3,2] 。
而对于 sequences = [[1,2],[1,3],[1,2,3]] ,唯一可能的最短 超序列 是 [1,2,3] 。[1,2,3,4] 是可能的超序列,但不是最短的。
如果 nums 是序列的唯一最短 超序列 ,则返回 true ,否则返回 false 。
子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素,而不改变其余元素的顺序的序列。
示例 1:
输入:nums = [1,2,3], sequences = [[1,2],[1,3]]
输出:false
解释:有两种可能的超序列:[1,2,3]和[1,3,2]。
序列 [1,2] 是[1,2,3]和[1,3,2]的子序列。
序列 [1,3] 是[1,2,3]和[1,3,2]的子序列。
因为 nums 不是唯一最短的超序列,所以返回false。
示例 2:
输入:nums = [1,2,3], sequences = [[1,2]]
输出:false
解释:最短可能的超序列为 [1,2]。
序列 [1,2] 是它的子序列:[1,2]。
因为 nums 不是最短的超序列,所以返回false。
示例 3:
输入:nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]]
输出:true
解释:最短可能的超序列为[1,2,3]。
序列 [1,2] 是它的一个子序列:[1,2,3]。
序列 [1,3] 是它的一个子序列:[1,2,3]。
序列 [2,3] 是它的一个子序列:[1,2,3]。
因为 nums 是唯一最短的超序列,所以返回true。
提示:
n == nums.length
1 <= n <= 104
nums 是 [1, n] 范围内所有整数的排列
1 <= sequences.length <= 104
1 <= sequences[i].length <= 104
1 <= sum(sequences[i].length) <= 105
1 <= sequences[i][j] <= n
sequences 的所有数组都是 唯一 的
sequences[i] 是 nums 的一个子序列
我的方法:递归 to 循环
首先根据 sequences 建立邻接表edge (根据前后顺序)
依题意,我们只要根据nums,找到一条有向路线,即可满足要求,因此考虑递归(栈调用太深,超时) or 循环
class Solution:
def sequenceReconstruction(self, nums: List[int], sequences: List[List[int]]) -> bool:
if len(sequences)==1:
return nums==sequences[0]
from collections import defaultdict
edge = defaultdict(list)
for it in sequences:
for i in range(1, len(it)):
edge[it[i-1]].append(it[i])
ans = [nums[0]]
idx = 0
while len(ans)!=len(nums):
cur = nums[idx]
for it in edge[cur]:
if it!=nums[idx+1]: continue
ans.append(it)
break
else:
return False
idx += 1
return True
复杂度:构建邻接表:O(m*n),搜索路径:O(len(nums)*n)
优化:edge 字典保存 set,而不是list
def sequenceReconstruction(self, nums: List[int], sequences: List[List[int]]) -> bool:
# 记录每个数的子结点
d = defaultdict(set)
for seq in sequences:
for i in range(1, len(seq)):
d[seq[i-1]].add(seq[i])
# 检查 nums 是否一条从头到尾的一条路径
for i in range(1, len(nums)):
if nums[i] not in d[nums[i-1]]:
return False
return True
复杂度:构建邻接表:O(m*n),搜索路径:O(len(nums))
(并查集) 剑指 Offer II 116. 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
示例 2:
输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
提示:
1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
class UF:
def __init__(self, n: int) -> None:
self.pa = [i for i in range(n)]
self.cnt = n
self.size = [1 for i in range(n)]
def findPa(self, x: int)->int:
while self.pa[x]!=x:
self.pa[x] = self.pa[self.pa[x]]
x = self.pa[x]
return x
def union(self, x: int, y: int):
paX = self.findPa(x)
paY = self.findPa(y)
if paX==paY: return
if self.size[paX]<=self.size[paY]:
self.pa[paX] = paY
self.size[paY] += self.size[paX]
else:
self.pa[paY] = paX
self.size[paX] += self.size[paY]
self.cnt -= 1
n = len(isConnected)
u = UF(n)
for i in range(n):
for j in range(i+1, n):
if isConnected[i][j]==1:
u.union(i, j)
return u.cnt
(并查集) 剑指 Offer II 117. 相似的字符串
如果交换字符串 X 中的两个不同位置的字母,使得它和字符串 Y 相等,那么称 X 和 Y 两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。
例如,“tars” 和 “rats” 是相似的 (交换 0 与 2 的位置); “rats” 和 “arts” 也是相似的,但是 “star” 不与 “tars”,“rats”,或 “arts” 相似。
总之,它们通过相似性形成了两个关联组:{“tars”, “rats”, “arts”} 和 {“star”}。注意,“tars” 和 “arts” 是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。
给定一个字符串列表 strs。列表中的每个字符串都是 strs 中其它所有字符串的一个 字母异位词 。请问 strs 中有多少个相似字符串组?
字母异位词(anagram),一种把某个字符串的字母的位置(顺序)加以改换所形成的新词。
示例 1:
输入:strs = ["tars","rats","arts","star"]
输出:2
示例 2:
输入:strs = ["omv","ovm"]
输出:1
提示:
1 <= strs.length <= 300
1 <= strs[i].length <= 300
strs[i] 只包含小写字母。
strs 中的所有单词都具有相同的长度,且是彼此的字母异位词。
class Solution:
def numSimilarGroups(self, strs: List[str]) -> int:
class UF:
def __init__(self, n: int) -> None:
self.pa = [i for i in range(n)]
self.cnt = n
self.size = [0] * n
def findPa(self, x: int)->int:
while x!=self.pa[x]:
self.pa[x] = self.pa[self.pa[x]]
x = self.pa[x]
return self.pa[x]
def union(self, x:int, y:int):
xPa = self.findPa(x)
yPa = self.findPa(y)
if xPa==yPa: return
if self.size[xPa]>=self.size[yPa]:
self.pa[yPa] = xPa
self.size[xPa] += self.size[yPa]
else:
self.pa[xPa] = yPa
self.size[yPa] += self.size[xPa]
self.cnt -= 1
n = len(strs)
uf = UF(n)
for i in range(n):
for j in range(i+1, n):
if strs[i]==strs[j]:
uf.union(i, j)
continue
cnt = 0
for it in range(len(strs[i])):
if strs[i][it]!=strs[j][it]:
cnt += 1
if cnt>2: break
if cnt==2: uf.union(i, j)
return uf.cnt
(并查集) 剑指 Offer II 118. 多余的边
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
示例 1:
输入: edges = [[1,2],[1,3],[2,3]]
输出: [2,3]
示例 2:
输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
输出: [1,4]
提示:
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

我的方法:并查集
遍历edges,当发现两个节点已经连通时,则该边可以被删除,记录当前节点的位置,此后不断更新该位置即可。
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
class UF:
def __init__(self, n: int) -> None:
self.pa = [i for i in range(n)]
self.size = [0] * n
def findPa(self, x: int)->int:
while x!=self.pa[x]:
self.pa[x] = self.pa[self.pa[x]]
x = self.pa[x]
return self.pa[x]
def union(self, x:int, y:int)->bool:
xPa = self.findPa(x)
yPa = self.findPa(y)
if xPa==yPa: return False
if self.size[xPa]>=self.size[yPa]:
self.pa[yPa] = xPa
self.size[xPa] += self.size[yPa]
else:
self.pa[xPa] = yPa
self.size[yPa] += self.size[xPa]
return True
n = len(edges)
u = UF(n)
pre = None
for i in range(n):
a, b = edges[i]
if not u.union(a-1, b-1):
pre = i
return edges[pre]
(并查集) 6135. 图中的最长环
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
示例 2:
输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
提示:
n == edges.length
2 <= n <= 105
-1 <= edges[i] < n
edges[i] != i
我的方法:并查集
与上一题思路一致,先用并查集判断出所有环的起点,然后遍历这些起点,记录环的长度
class Solution:
def longestCycle(self, edges: List[int]) -> int:
class UF:
def __init__(self, n: int) -> None:
self.pa = [i for i in range(n)]
self.cnt = n
self.size = [0] * n
def findPa(self, x: int)->int:
while x!=self.pa[x]:
self.pa[x] = self.pa[self.pa[x]]
x = self.pa[x]
return self.pa[x]
def union(self, x:int, y:int)->bool:
xPa = self.findPa(x)
yPa = self.findPa(y)
if xPa==yPa: return False
if self.size[xPa]>=self.size[yPa]:
self.pa[yPa] = xPa
self.size[xPa] += self.size[yPa]
else:
self.pa[xPa] = yPa
self.size[yPa] += self.size[xPa]
self.cnt -= 1
return True
n = len(edges)
u = UF(n)
lst = []
for i in range(n): # 记录所有环的起点
if edges[i]!=-1 and not u.union(i, edges[i]):
lst.append(edges[i])
ans = -1
for cur in lst: # 遍历环起点,更新最大长度
target = cur
cur = edges[cur]
tmp = 1
while cur!=target:
cur = edges[cur]
tmp += 1
ans = max(ans, tmp)
return ans
剑指 Offer II 119. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 104
-109 <= nums[i] <= 109
并查集
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
if len(nums)==0: return 0
nums = list(set(nums))
nums.sort()
n = len(nums)
pa = list(range(n))
size = [1]*n
self.ans = 1
def find(x: int)->int:
while x!=pa[x]:
pa[x] = pa[pa[x]]
x = pa[x]
return x
def union(x: int, y:int):
xPa = find(x)
yPa = find(y)
if xPa==yPa: return
if size[xPa]>=size[yPa]:
pa[yPa] = xPa
size[xPa] += size[yPa]
self.ans = max(self.ans, size[xPa])
else:
pa[xPa] = yPa
size[yPa] += size[xPa]
self.ans = max(self.ans, size[yPa])
for i in range(1, n):
if abs(nums[i] - nums[i-1])==1:
union(i, i-1)
return self.ans
SortedSet
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
if len(nums)==0: return 0
from sortedcontainers import SortedSet
vis = SortedSet(nums)
ans = 1
tmp = 1
for it in vis:
if it+1 in vis :
tmp += 1
ans = max(ans, tmp)
else:
tmp = 1
return ans
进阶:可以设计并实现时间复杂度为 O(n) 的解决方案吗?
哈希表 + 逻辑
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
if len(nums)==0: return 0
vis = set(nums)
ans = 1
for it in vis:
if it-1 not in vis: # ,只有起始值可以进入
cur = it
tmp = 1
while cur+1 in vis:
tmp+=1
cur = cur+1
ans = max(ans, tmp)
return ans
复杂度:O(n)
最小生成树 = (费用排序+并查集)
1584. 连接所有点的最小费用
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出:20
解释:
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]]
输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]]
输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]]
输出:4000000
示例 5:
输入:points = [[0,0]]
输出:0
提示:
1 <= points.length <= 1000
-106 <= xi, yi <= 106
所有点 (xi, yi) 两两不同。
kruskal 算法
分成三步:
- 构建所有权重边,这道题每两个点之间都可以看做是有一条边,所以,一共是 n ∗ ( n − 1 ) 2 \frac{n*(n-1)}{2} 2n∗(n−1) 条边;
- 按权重边排序;
- 使用并查集来构造最小生成树,并查集主要用来判断两个是否是已经连通的状态;
- 如果未联通,则直接联通
- 否则,跳过(说明之前已经建立了最小权重的边了)
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
n = len(points)
edge = []
for i in range(n):
for j in range(i+1, n): # 1
dist = abs(points[i][0]-points[j][0])+abs(points[i][1]-points[j][1])
edge.append((dist, i, j))
edge.sort() # 2
# Union Set
pa = list(range(n))
cnt = [n]
size = [1]*n
def find(x: int)->int:
while x!=pa[x]:
pa[x] = pa[pa[x]]
x = pa[x]
return x
def union(x: int, y: int):
xPa = find(x)
yPa = find(y)
if xPa==yPa:
return True
if size[xPa]<size[yPa]:
pa[xPa] = yPa
size[yPa] += size[xPa]
else:
pa[yPa] = xPa
size[xPa] += size[yPa]
cnt[0] -= 1
return False
ans = 0
for dist, x, y in edge:
if not union(x, y): # 3 如果未建立链接,则连通
ans += dist
return ans
迪杰斯特拉 单源带权最小路
1514. 概率最大的路径
给你一个由 n 个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为 succProb[i] 。
指定两个节点分别作为起点 start 和终点 end ,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。
如果不存在从 start 到 end 的路径,请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ,就会被视作正确答案。
示例 1:
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出:0.25000
解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25
示例 2:
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出:0.30000
示例 3:
输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出:0.00000
解释:节点 0 和 节点 2 之间不存在路径
提示:
2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边
优先队列+BFS
队列存两个值,(dist, cur)
使用 优先队列代替queue,优先拿出 dist 较大(小)的路径进行遍历,可以优化复杂度
def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:
from collections import defaultdict
from queue import PriorityQueue
weightEdge = defaultdict(list)
for i, (s, e) in enumerate(edges):
weightEdge[s].append((e, succProb[i]))
weightEdge[e].append((s, succProb[i]))
vis = set()
q = PriorityQueue()
q.put((-1., start))
ans = 0.
while not q.empty():
p, cur = q.get()
p = -p
vis.add(cur)
for nxt, prob in weightEdge[cur]:
newDist = p*prob
if newDist<ans:
continue
if nxt==end:
ans = max(ans, newDist)
if nxt in vis: continue
q.put((-newDist, nxt))
return ans