模块二:线性直流电阻电路分析原理与方法
等效法
1、无缘网络的等效变换
一端口网络:任一复杂电路通过两个连接端钮与外电路相连,这样具有两个端钮的网络即称为一端口网络或者二端钮网络
A-有源;P-无源;N-有源,无源;
等效变换的条件:两个内部结构完全不同的一端口网络p1,p2,如果他们端口上的电压与电流之间的伏案特性完全相同,则称为两者等效;
串联电阻相加,并联电导相加;
星型连接可以与三角型连接相互转换;
2、电压源与电流源的等效变换
电压源:U=E-IR
电流源:U=RIs-RI
故等效条件是:E=RIs
方程法
目标:同时求解一组电路变量(支路电压或者电流)
问题:如何选取一组合适的方程(方程数与变量数相等,方程组线性无关,具有唯一解)
基础:基尔霍夫电压定律和电流定律,以及元件电压电流关系。
方法:通过网络图论来选取合适的方程组{支路电流法、网孔电流法和节点电压法)
网络图论初步
电路图:由集中参数元件组成的电网络
拓扑图:由线条(支路)和点(节点)所组成的图形,称此图为原电网络的拓扑图,简称为图
有向图:线图各支路规定了一个方向(用箭头表示,一般取电路图中支路电流方向一致)
回路:从一个节点出发,经过若干条支路后,又回到这个节点的通路
网孔回路:回路内无任何支路,则此回路称为网孔回路
当图的任二节点之间至少存在一条通路时,称为连通图,否则称为非连通图
连通图任二个节点之间至少存在一个回路,则称为不可分图,否则为可分图
如果图能无任何交叉地画在平面上,则称为平面图,否则为非平面图
树T时有向图G的一个子图,它包含所有节点与一些支路的集合。树T满足三个条件:T是连通的;包含G的全部节点;不包含回路。(有向树图的选择不是唯一的,一般可以选出多个树)
树T所包含的支路称为树支;有向图G中其余的支路称为连支;树支数=n-1(节点数减一);连支数=支路数-树支数=b-n+1=l(网孔数)
割集Q连通图G的一个子图,满足:若移去Q中全部支路,原连通图G将被分为两个独立部分;若少移去Q中任意一条支路,原连通图G将保持连通
单连支回路:每一连支可与其两端之间的唯一树支路径构成一条唯一的回路。此回路称为单连支回路。回路方向与连支方向一致。
单连支回路一定可以写出独立的KVL方程;独立的KVL方程不一定要按照单连支回路来写
单树支割集:组成割集的支路仅含一条树支。割集方向与树支方向一致。
单树支割集一定可以写出独立的KCL方程;独立的KCL方程不一定要按照单树支割集来写
b:表示支路数
n:表示节点数
l:表示网孔数
支路电流法
支路法:以各支路电流和电压为未知量列写电路方程分析电路
支路电流法的一般步骤:
标定各支路电流的参考方向;选定(n-1)个节点,列写KCL方程;选定b-(n-1)个独立回路,列写KVL方程;(元件特性带入);求解上述方程,得到b个支路电流;进一步计算支路电压和进行其他分析
支路电流法的特点:支路电流法简单但要求同时列写KCL和KVL方程,方程数较多,且规律性不强(相对于后面的方法),手工求解比较复杂,便于计算机编程求解。
网孔回路法
基本思想:假想每个回路中有一个回路电流。则各支路电流可用回路电流线性组合表示
回路法的一般步骤:
选定l=b-(n-1)个独立回路,并确定其绕行方向;对l个独立回路,以回路电流为未知量,列出其KVL方程;求解上述方程,得到l个回路电流;求各支路电流(用回路电流表示);其他分析
网孔电流法:对平面电路,若以网孔为独立回路,此时回路电流也成为网孔电流,对应分析方法称为网孔电流法
节点电压法
节点电压(位):节点与参考点的电压差,方向为从独立节点指向参考节点。
节点电压法:以节点电压为未知量列写电路方程的方法。
节点电压法的独立方程数为(n-1)个。与支路电流法相比,方程数可减少b-(n-1)个。
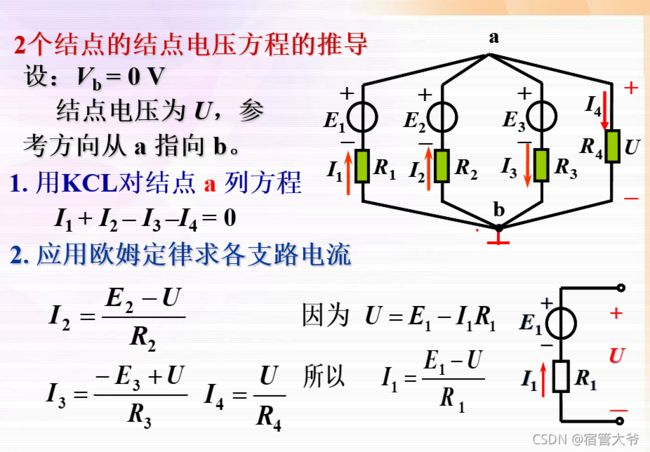
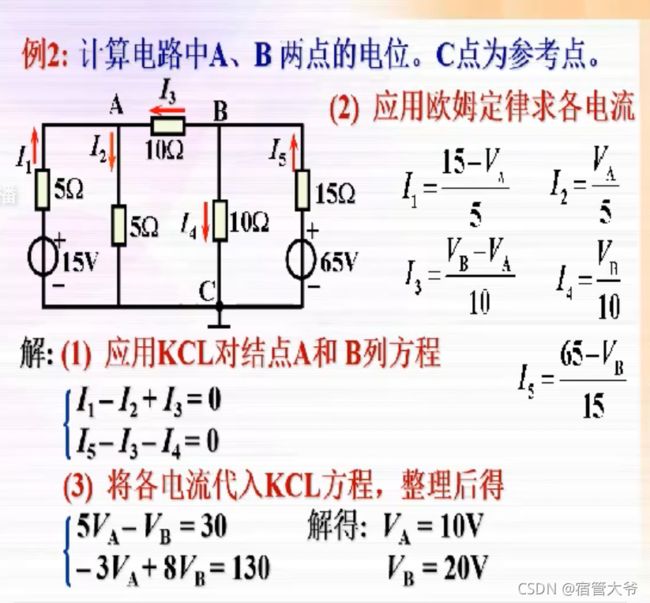
适用于两个节点的节点电压公式:
一般性节点电压法
列出(n-1)个电流方程,选定参考点(电位为零),用各点的电位来表示电流。
电路定理
叠加定理
定义:在线性电路中,任一支路电流(或电压)都是电路中各个独立电源单独作用时,在该支路产生的电流(或电压)的代数和。
单独作用:一个独立电源作用,其余独立电源不作用。不作用是指电压源u=0(短路),电流源i=0(开路)。
*功率不能叠加,只有线性变量可以运用叠加定理;含受控源(线性)电路亦可用叠加法,但受控源不能单独作用,应始终保留在电路中。
齐性原理
定义:当电路中只有一个激励(独立源)时,则响应(电压或电流)与激励成正比。
替代定理
定义:任意一个电路,其中第K条支路的电压已知为uk(电流为ik),那么就可以用一个电压等于uk的理想电压源(电流等于ik的独立电流源)来替代该支路,替代前后电路中各处电压和电流均保持不变。
注意:1)替代定理适用于线性、非线性电路、定常和时变电路。
2)替代定理的应用必须满足:原电路和替代后的电路必须有唯一解;被替代的支路和电路其他部分应无耦合关系。
3)未被代替的支路的相互连接及参数不能改变。
戴维南(诺顿)定理
二端网络:具有两个出线端的部分电路
无源二端网络:二端网络中没有电源(可简化为一个电阻)
有源二端网络:二端网络中含有电源
定义:任何一个含独立电源、线性电阻和线性受控源的二端口,对外电路来说,可以用一个电压Ud和电阻Rd的串联组合来等效代替:
电压源Ud:外电路 断开时端口处的开路电压:
电阻Rd:一端口中全部独立电源置零后的端口等效电阻。
注意:1)戴维南等效电路中电压源电压等于将外电路断开时的开路电压Ud,电压源方向与所求开路电压方向相同。
2)串联电阻为将一端口内部独立电源全部置零(电压源短路,电流源开路)后,所得一端口网络的等效电阻。
3)当一端口内部含有受控源时,控制支路与受控源支路必须包含在等效变换的同一部分电路中。
等效电阻的计算方法:1)电阻串并联公式:网络内部不含有受控源;
2)加源法:端口(内部独立电源置零)加电压求电流法或加电流求电压法;
3)开路短路法:等效电阻Rd=端口的开路电压Ud/短路电流Id。
最大功率传输定理
定义:线性有源一端口网络向可变电阻负载Rl传输最大功率的条件是:Rl=Rd。
当Rl=Rd时,负载获得最大功率。也称为功率匹配。匹配状态下,功率的传输效率只有百分之五十。经常出现在电子线路中。对于电路传输系统的输、配电线路,传输功率大,要求传输效率高,以减少传输过程中的能量损耗,因此都不在匹配状态下工作。