17.python实现最小生成树-普里姆算法

最小生成树

一个有 n 个结点的带权无向图，在满足所有顶点都连接的前提下使得所有的边的权总和最小，即为最小生成树(Minimum Spanning Tree MST)。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

1. N个顶点，一定有N-1条边
2. 包含所有顶点
3. 所有顶点都可以直接或间接连接到另外的顶点

普里姆算法

普里姆算法在找最小生成树时，将顶点分为两类，一类是在查找的过程中已经包含在树中的（假设为 A 类），剩下的是另一类（假设为 B 类）。

对于给定的连通网，起始状态全部顶点都归为 B 类。在找最小生成树时，选定任意一个顶点作为起始点，并将之从 B 类移至 A 类；然后找出 B 类中到 A 类中的顶点之间权值最小的顶点，将之从 B 类移至 A 类，如此重复，直到 B 类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。

1. 创建一个VisitedList保存所有已经被访问过的顶点
2. 从任意顶点A开始构建最小生成树，标记顶点V已经被访问，加入被访问过顶点集合VisitedList
3. 遍历被访问顶点集合 找到在不构成回路的前提下权值最小的边，将新增的顶点加入VisitedList
4. 循环直到为顶点-1条边构建完成

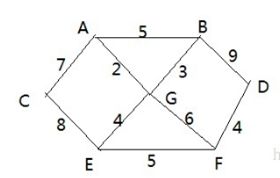
图解

1.从顶点开始处理  ======>  2
A-C [7] A-G[2] A-B[5] => 

2.  开始 , 将A 和 G 顶点和他们相邻的还没有访问的顶点进行处理 =》
A-C[7] A-B[5]  G-B[3] G-E[4] G-F[6]

3.  开始，将A,G,B 顶点 和他们相邻的还没有访问的顶点进行处理=>
A-C[7] G-E[4] G-F[6] B-D[9] 
.....
4.{A,G,B,E}->F//第4次大循环 ，  对应 边 权值：5
5.{A,G,B,E,F}->D//第5次大循环 ， 对应 边 权值：4

4. {A,G,B,E,F,D}->C//第6次大循环 ， 对应 边 权值：7 ===> 

class MiniTree(object):
    def __init__(self, vertex, weight):
        """
        最小生成树
        """
        self.vertex = vertex
        self.weight = weight

    def create_mini_tree(self, start):
        """
        最小生成树
        :param start:
        :return:
        """
        visited = []
        # 标记已访问
        visited.append(start)
        v1, v2 = None, None
        while len(visited) < len(self.vertex):
            min_weight = float('inf')
            for v in visited:
                for i in range(len(self.vertex)):
                    # 边没有被访问过且 权重较小
                    if i not in visited and self.weight[v][i] < min_weight:
                        v1 = v
                        v2 = i
                        min_weight = self.weight[v][i]
            visited.append(v2)
            print('%s -> %s weight = %d' % (self.vertex[v1], self.vertex[v2], self.weight[v1][v2]))


if __name__ == '__main__':
    mini_tree = MiniTree(['A', 'B', 'C', 'D', 'E', 'F', 'G'],
                         [[10000, 5, 7, 10000, 10000, 10000, 2], [5, 10000, 10000, 9, 10000, 10000, 3],
                          [7, 10000, 10000, 10000, 8, 10000, 10000], [10000, 9, 10000, 10000, 10000, 4, 10000],
                          [10000, 10000, 8, 10000, 10000, 5, 4], [10000, 10000, 10000, 4, 5, 10000, 6],
                          [2, 3, 10000, 10000, 4, 6, 10000], ])
    mini_tree.create_mini_tree(0)