K均值聚类分析流程

K均值聚类分析流程

一、案例背景

在某体育赛事中，意大利、韩国、罗马尼亚、法国、中国、美国、俄罗斯七个国家的裁判对300名运动员进行评分，现在想要通过评分上的差异将300名选手进行分类，计划将选手分为高水平、中水平、低水平三个类别。因为评分均为定量数据，所以通过K均值聚类进行聚类分析，部分数据如下：

二、异常值检查

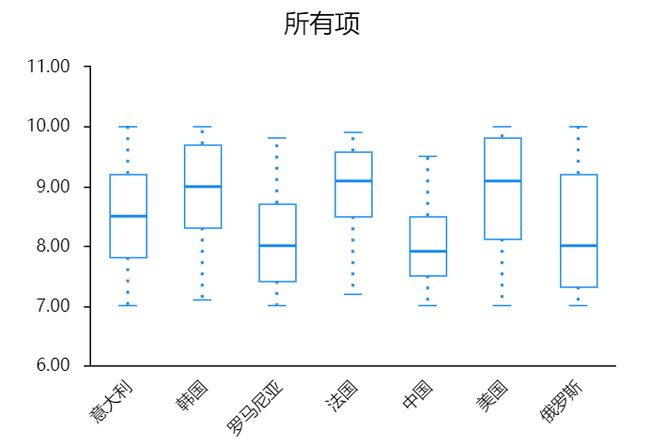
异常值对于聚类分析的结果影响比较大，所以在分析之前要先进行异常值的检查。异常值检查的方法有很多种，比如可以使用描述统计法，查看是否有三倍标准差外的数据，或者使用箱线图，直观查看是否存在异常值，本案例使用SPSSAU箱线图进行异常值检查，输出结果如下：

从箱线图分析结果来看，7个裁判的评分均没有异常值出现，都在规定范围之内（最低7分，最高10分），可以进行接下来的K均值聚类分析。

三、K均值聚类分析

K均值聚类是现在比较常用的聚类算法之一，接下来分别对该方法的原理和操作进行简单的说明，帮助大家更好的理解聚类分析的过程。

（1）基本说明

K均值聚类也称K-means聚类，是典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。因为需要计算距离，所以决定了K-means算法只能处理数值型数据，而不能处理分类属性型数据。

K均值聚类分析算法步骤：

① K-means算法首先需要选择K个初始化聚类中心

② 计算每个数据对象到K个初始化聚类中心的距离，将数据对象分到距离聚类中心最近的那个数据集中，当所有数据对象都划分以后，就形成了K个数据集（即K个簇）

③ 接下来重新计算每个簇的数据对象的均值，将均值作为新的聚类中心

④ 最后计算每个数据对象到新的K个初始化聚类中心的距离，重新划分

⑤ 每次划分以后，都需要重新计算初始化聚类中心，一直重复这个过程，直到所有的数据对象无法更新到其他的数据集中。

（2）操作

在SPSSAU系统中，以上算法步骤都自动进行，只需要分析人员将数据拖拽到分析框中，选择聚类数量即可，如下图：

通常情况下，建议聚类个数为3~6个比较好，SPSSAU默认聚类个数为3，本案例，预设将300名选手分为高、中、低3个类别，所以选择默认聚类个数3即可。因为K均值聚类是根据距离进行类别判断，所以需要消除量纲（单位）的影响，SPSSAU系统默认对聚类数据进行【标准化】处理，如果不需要进行标准化处理，可以选择取消勾选。同时SPSSAU默认【保存类别】，将聚类结束后，聚类的类别变量自动保存下来，用于后续分析。

四、聚类分析结果解读

K均值聚类分析（以下简称聚类分析）结果可以从以下几个方面进行分析：聚类基本情况、聚类类别命名、聚类中心、聚类效果图示化；接下来将逐个进行说明。

（1）聚类基本情况

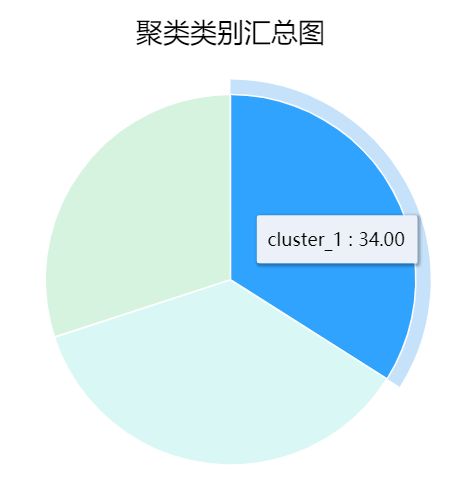
SPSSAU输出聚类类别基本情况汇总表如下：

上表描述了聚类分析的基本情况，展示了本次聚类分析共得出3类，SPSSAU自动命名为cluster_1、cluster_2、cluster_3；同时展示每个类别人群数量和比例情况。这3类群体的占比分别是34.00%,、36.00%、 30.00%。整体来看，3类人群分布较为均匀，整体说明聚类效果较好。SPSSAU同时会输出聚类类别汇总图，方便分析人员更加直观的展示聚类类别占比情况。

（2）聚类类别命名

得到聚类结果后，需要根据各个聚类类别的特征进行类别命名。

为了得到各个类别之间的差异，使用方差分析进行聚类类别的差异对比分析，然后根据各个类别的差异性特征进行聚类类别的命名。

从上表聚类类别方差分析差异对比结果来看，7个裁判对于3个类别的评分之间均存在差异性（p<0.05），说明聚类分析得到的3个群体他们在研究的特征上具有明显的差异性，也能从一定程度上说明本次聚类分析效果较好。3个聚类类别的具体差异性可通过评分的平均值进行对比，并对聚类类别进行命名。

从3个类别的评分平均值来看，结合前面预设将300名选手分为高水平、中水平、低水平3类，故将cluster_1命名为低水平、cluster_2命名为中水平、cluster_3命名为高水平。SPSSAU可使用数据处理中的【数据标签】功能，进行命名，操作如下：

（3）聚类中心

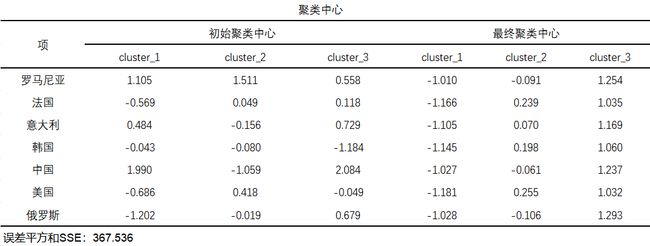
前面我们通俗介绍了K均值聚类分析的聚类过程，提到初始聚类中心，在迭代过程中最后会成为最终聚类中心点，这个结果SPSSAU也为大家提供了，见下表：

聚类中心是聚类算法的数学理论或中间过程指标，针对分析来看其实际意义较小。一般来讲相较于聚类中心，K均值聚类更关注误差平方和SSE值。该值可用于测量各点与中心点的距离情况，理论上是希望越小越好，通常用于辅助判断聚类个数。如果在开始分析之初，不确定聚类个数，那么可以多次分析选择不同聚类个数，对比分析SSE值，比如发现从3个聚类个数到4个聚类个数时SSE值减少幅度明显很大，那么此时选择4个聚类类个数较好。但聚类类别并不是越多越好，还需要结合专业知识进行判断。

（4）聚类效果可视化

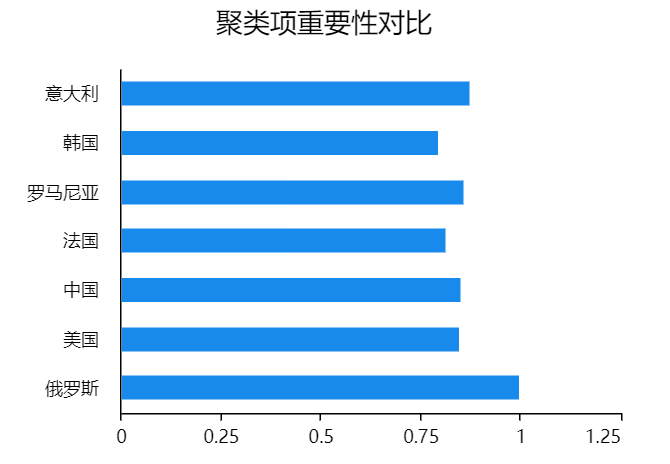
除了使用表格展示聚类分析的结果，还可以通过图示化展示聚类项重要性，如下图：

聚类分析以多个研究指标作为基准，对样本进行分类。每个指标对于聚类的贡献不一样， 具体贡献大小对比可见上图。如果某项的贡献明显非常低，可考虑将该项移除后重新进行聚类分析。

可以通过使用散点图直观展示聚类效果，使用任意两个聚类指标进行散点图绘制，并且在颜色区分(定类)框中放入“聚类类别”项（SPSSAU自动保存的聚类类别），以查看不同类别时，两两指标的散点效果。SPSSAU操作如下：

比如使用罗纳尼亚和韩国进行散点图绘制，在颜色区分框中放入聚类类别，SPSSAU输出散点图如下：

从上图来看，3个类别之间虽然有些部分存在交叉，但是绝大部分类别的划分都有明显的区别，说明本次聚类分析效果较好。

五、总结

首先使用箱线图对数据进行异常值检查，确保不存在异常数据后，进行K均值聚类分析。通过7位裁判的打分，将300位选手最终划分为高水平、中水平、低水平3类。从聚类分析基本情况、聚类类别方差分析差异对比结果以及聚类效果散点图分析来看，本次聚类分析效果较好，聚类结果比较可靠。