SWUST oj 446: 合并排序

446: 合并排序

题目描述

这是一个很简单的排序题目. 为了锻炼大家对不同算法的了解,请大家用归并排序法对此题进行解答. 对一组整数数列A[1],A[2],A[3]…A[N]进行排序,按照从小到大的顺序输出.

输入

本题只有一组测试数据,在输入的第一行输入N(表示整数数列的大小)(N ＜ 1000)
接下来N行输入N个整数,每一行一个整数.

输出

对已经排好序的数从小到大依次输出,每两个数之间用两个空格隔开,且每输出10个数换行.
样例输入

12
45 
545 
48 
47 
44 
45 
4857 
58 
57 
485 
1255 
42

样例输出

42 44 45 45 47 48 57 58 485 545
1255 4857

解释

1_5_3_7_9_1_4_2 第一次划分
1_5_3_7 | 9_1_4_2 第二次划分 以第一次划分为最右边
1_5 | 3_7 | 9_1_4_2 第三次划分 以第二次划分为最右，为什么还可以划分因为你的判断条件是left 1_5 | 3_7 | 9_1_4_2 第四次划分以第三次划分为最右
1 | 5 | 3_7 | 9_1_4_2 这里 以第三次划分为最右的第四次划分就完成了，然后回溯，以第二次划分为最左，为什么？因为左边划分完成了，现在进行右边划分，此时的右边是第二次划分的右边到第一次划分的左边部分，
1 | 5 | 3 | 7 | 9_1_4_2 第五次划分完成的结果。好了现在左边部分就完成了

。。。。。。。 这里我们省略右边部分的划分

开始排序，左右两边划分完成后，我们开始排序
首先我们来看递归树

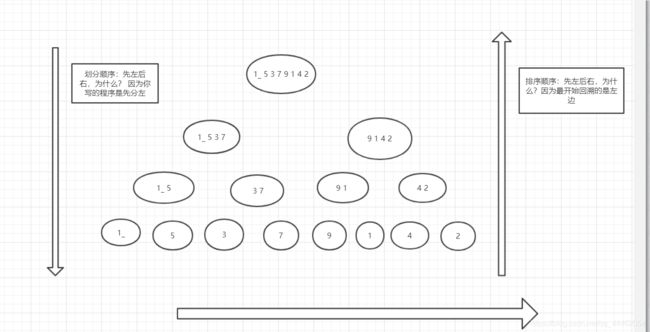
左边部分：
1_5_3_7_9_1_4_2
1_5_3_7 | 9_1_4_2
1_5 | 3_7 | 9_1_4_2
1 | 5 | 3_7 | 9_1_4_2
1 | 5 | 3 | 7 | 9_1_4_2

排序时，最开始的排序是什么？ 就是我们两部分划分完成，才开始排序，排序的时候，左边部分先开始排序，为什么？ 参考递归算法的图解。
所以 1 5 进行排序，然后3 7 开始排序 然后 1 5 3 7 开始排序 得到左边部分的顺序1_ 3 5 7

然后右边部分： 9 1 排序 4 2 排序 然后1 9 2 4开始排序 得到右边部分的顺序 1 2 4 9
现在最后一次回溯：1_ 3 5 7 |1 2 4 9 (第一次划分结果) 得到 1_ 1 2 3 4 5 7 9 （完成排序）

#include
#include
void merge(int a[],int left,int mid,int right){
	int b[mid-left+1];//划分后的左边数组大小
	int c[right-mid]; //划分后的右边数组大小 
	int i,j,k;
	int lenb=0; 
	int lenc=0;
	for(i=left;i<=mid;i++){//左边数组赋值 
		b[lenb++]=a[i];
	}
	for( j=mid+1;j<=right;j++){//右边数组赋值 
		c[lenc++]=a[j];
	}
	i=0; 
	j=0; 
	k=left;//a[]下标起始应该为k=left 因为 是 left~right这个范围里进行合并排序 
	//开始合并
	while(i<lenb&&j<lenc){//这里合并就这样判断逻辑要清楚一点 
		if(b[i]>c[j]){//左边大 
			a[k]=c[j++];
		}else if(b[i]<c[j]){
			a[k]=b[i++];
		}else {
			a[k]=b[i++];
			k++;
			a[k]=c[j++];
		}
		k++;	
	}
	while(i<lenb){//假设 c[]已经遍历完了 b[]还没有 说明剩下的b[]都是大于c[]的
		a[k]=b[i++];
		k++;
	}
	while(j<lenc){// 假设b[]数组已经遍历完了  c[]还没有 说明剩下的c[]都是大于b[]
		a[k]=c[j++];
		k++;
	}
}
void mergeSort(int a[],int left,int right){
	if(left<right){
		int mid=left+((right-left)>>1);//>>1 表示除以2 比 / 运算符更快 
		mergeSort(a,left,mid);//继续划分左边 
		mergeSort(a,mid+1,right);//继续划分右边 
		merge(a,left,mid,right);//划分完成后开始合并，这个函数是 一次合并，回溯。 
	}else{
		return ;
	}
}
int main(){
	int n;
	int a[5005]={0};
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%d",&a[i]);
	}
	mergeSort(a,0,n-1);
	for(int i=0;i<n;i++){
		if((i+1)%10==0){
			printf("%d\n",a[i]);
		}else{
			if(i==n-1){
				printf("%d\n",a[i]);
			}else{
				printf("%d  ",a[i]);
			}
		}
	}
	return 0;
}