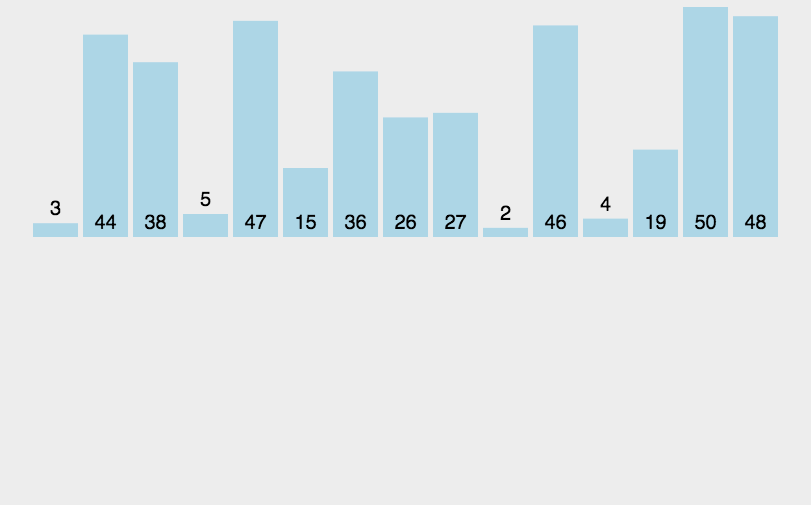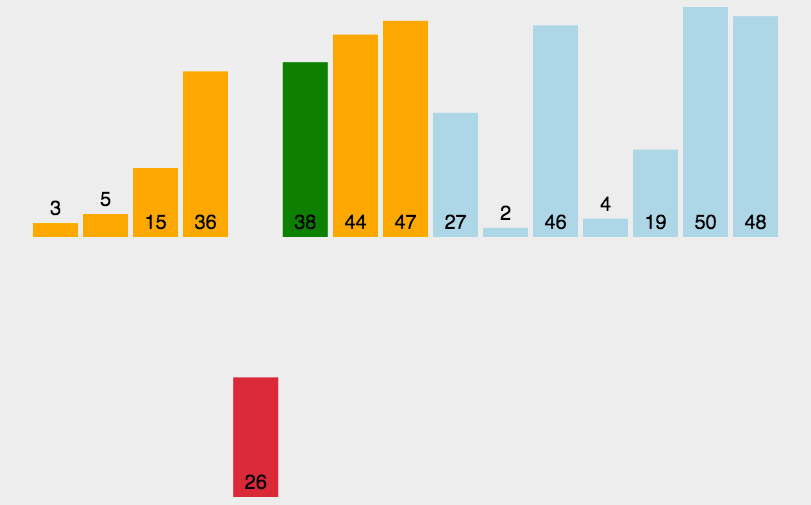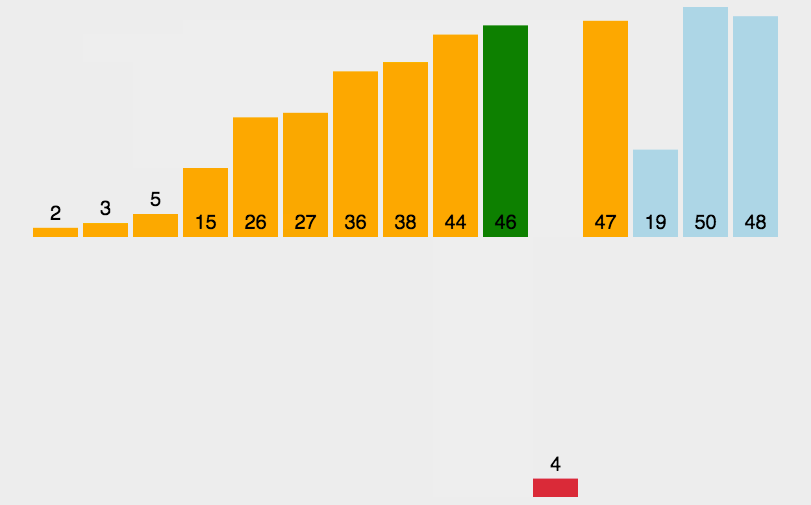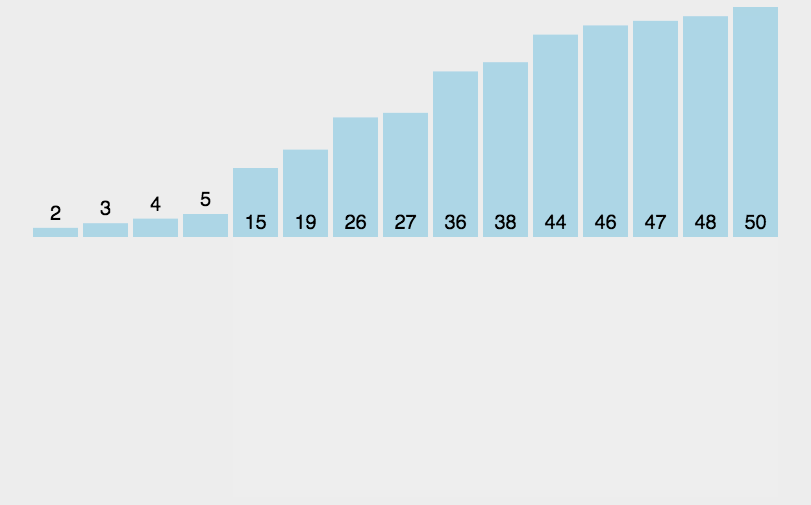
排序(1)之插入排序
目录
前言
插入排序
1.直接插入排序
1.1 直接插入排序实现
1.2 直接插入排序特性总结
2.希尔排序
2.1 希尔排序实现
2.2 希尔排序特性总结
前言
从今天小编就开始给大家介绍排序的内容,对于排序内容我们一共分,插入,选择,交换,归并这几个大类,那么今天小编给大家带来的就是插入排序
插入排序
1.直接插入排序
1.1 直接插入排序实现
具体如下:
这里我们看代码实现:
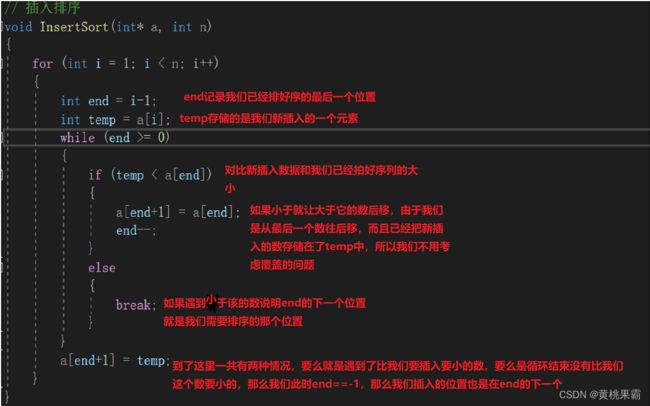
void InsertSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
int end = i-1;
int temp = a[i];
while (end >= 0)
{
if (temp < a[end])
{
a[end+1] = a[end];
end--;
}
else
{
break;
}
}
a[end+1] = temp;
}
}对于大思路,我相信大家已经理解了,但是对于代码的实现,这里我们还需要把控住一些细节
这里我给大家讲解一下
这里我们再实现一个打印数组的函数,对我们的插入排序进行测试。
void printArray(int*a,int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}这里看看结果如何
int main()
{
int arr[10] = { 1,22,31,45,67,34,35,47,39,49 };
int size = sizeof(arr) / sizeof(int);
InsertSort(arr, size);
printArray(arr, size);
}运行如下:
1.2 直接插入排序特性总结
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
说明:这也是我们直接插入的排序的优势,但是如果数据是顺序存储的,也需要我们遍历一遍后才知道相应结果,所以这里我们最好的情况下时间复杂度也是O(N)。
2. 时间复杂度:O(N^2)
说明:对于最好情况下我们这里的时间复杂度是O(N),但是由于时间复杂度是计算最坏情况下的时间复杂度,也就是该完全逆序存储,那么这里我们对于每个新插入的元素我们都需要插入到我们之前排好序的序列之前,所以这里的时间复杂度也就是O(N^2)。
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
对于稳定性,小编之后会给大家另写一篇介绍,这里大家先了解一下。
2.希尔排序
2.1 希尔排序实现
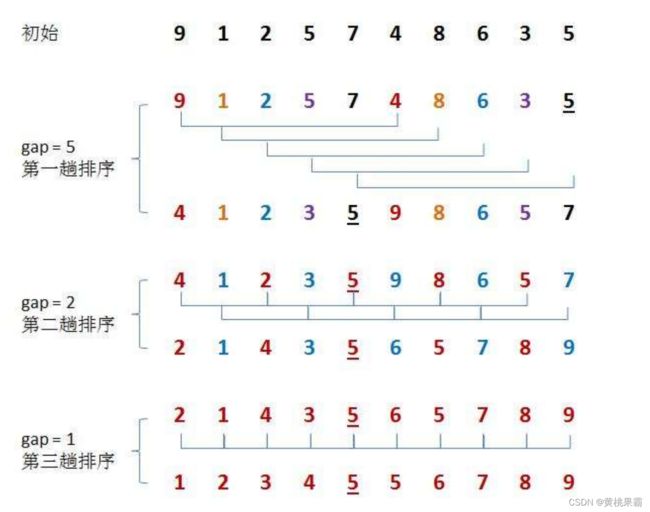
希尔排序一共分为两个步骤:
1.首先进行预排序(分组插排),让元素接近有序
2.直接进行插入排序
当gap>1时,我们的目的是让我们的数组接近有序,从某种意义上来讲,也就是将数组接近有序,但是当gap==1时,我们实际上进行的也是直接插入排序,但是经过之前的预排序,我们的数组已经接近有序,所以我们这里的插入排序我们就可以把它当作最好的情况处理,时间复杂度也到达了O(N)这个量级。
那么我们具体代码如下:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap >1)
{
gap = gap / 2;
for (int i = 0; i = 0)
{
if (temp < a[end])
{
a[end+gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end+gap] = temp;
}
}
} 这里我给大家讲解一下:
1.首先对于while的循环终止条件,对于希尔排序,我们进行的最后一趟一定是直接插入排序,所以就要求我们gap==1,所以我们在gap=gap/2,使得gap==1时,我们进行最后一趟排序,然后由于gap>1,我们退出循环,此时我们排序完成
2.由于希尔排序最后一趟进行的一定是插入排序,而这里我们有两种方式使得,该最后一趟为1,首先是gap=gap/2,然后就是为gap=gap/3+1.
3.然后是对于for循环的解释了,可能大家第一眼对这个循环的意思有点不理解,这里我给大家说明一下。
这里先给大家介绍一下另外一种写法:
这种写法估计大家比较好理解。
然后我给大家介绍一下,我们上面那种写法
以上两种大家应该可以发现,实际上该与直接插入排序没有多大变化,只是因为gap发生了改变。
这里我们测试一下。
int main()
{
int arr[10] = { 1,22,31,45,67,34,35,47,39,49 };
int size = sizeof(arr) / sizeof(int);
ShellSort(arr, size);
printArray(arr, size);
}运行结果如下:
2.2 希尔排序特性总结