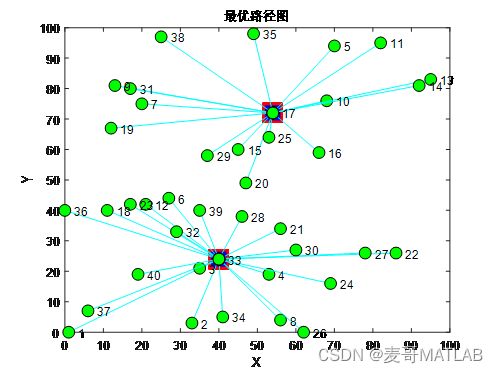
MATLAB差分进化算法求解超市物流配送选址问题实例

差分进化算法编程问题实例：

MATLAB差分进化算法求解超市物流配送中心选址问题代码实例

在范围为(0,0)到(100，100)的矩形区域内，散布着40个连锁超市，各个连锁超市的坐标及需求量见表1。要求在该矩形区域内确定N个位置建立配送中心。已知各配送中心容量不限，每个超市只由一个配送中心负责配送，使得N个配送中心到所有超市的总配送物流量（距离×需求量）最小，其中配送中心到超市的距离为直线距离。请建立该问题的模型，利用差分进化算法编程求解上述问题。
N可以取2，3，4，5，6，…等
表1 各需求点坐标及需求量
No. 坐标 需求量 No. 坐标 需求量 No. 坐标 需求量 No. 坐标 需求量
1 (1,0) 10 11 (82,95) 30 21 (56,34) 70 31 (17,80) 90
2 (33,3) 10 12 (21,42) 40 22 (86,26) 20 32 (29,33) 50
3 (35,21) 40 13 (95,83) 30 23 (17,42) 10 33 (40,24) 20
4 (53,19) 10 14 (92,81) 20 24 (69,16) 20 34 (41,5) 40
5 (70,94) 40 15 (45,60) 20 25 (53,64) 30 35 (49,98) 10
6 (27,44) 30 16 (66,59) 30 26 (62,0) 30 36 (0,40) 40
7 (10,69) 10 17 (54,72) 20 27 (78,26) 30 37 (6,7) 20
8 (56,4) 20 18 (11,40) 10 28 (46,38) 20 38 (25,97) 20
9 (16,81) 40 19 (12,67) 20 29 (37,58) 50 39 (35,40) 30
10 (68,76) 30 20 (47,49) 30 30 (60,27) 30 40 (19,19) 50

2 求解模型的差分进化算法设计
Differential Evolution（DE）是由Storn等人于1995年提出的，和其它演化算法一样，DE是一种模拟生物进化的随机模型，通过反复迭代，使得那些适应环境的个体被保存了下来。但相比于进化算法，DE保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性。同时，DE特有的记忆能力使其可以动态跟踪当前的搜索情况，以调整其搜索策略，具有较强的全局收敛能力和鲁棒性，且不需要借助问题的特征信息，适于求解一些利用常规的数学规划方法所无法求解的复杂环境中的优化问题。目前，DE已经在许多领域得到了应用，譬如人工神经元网络、化工、电力、机械设计、机器人、信号处理、生物信息、经济学、现代农业、食品安全、环境保护和运筹学等。
DE 算法主要用于求解连续变量的全局优化问题，其主要工作步骤与其他进化算法基本一致，主要包括变异(Mutation)、交叉(Crossover)、选择(Selection)三种操作。算法的基本思想是从某一随机产生的初始群体开始，利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照一定的规则与第三个个体求和而产生变异个体，该操作称为变异。然后，变异个体与某个预先决定的目标个体进行参数混合，生成试验个体，这一过程称之为交叉。如果试验个体的适应度值优于目标个体的适应度值，则在下一代中试验个体取代目标个体，否则目标个体仍保存下来，该操作称为选择。在每一代的进化过程中，每一个体矢量作为目标个体一次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局最优解逼近。

二、差分进化算法的流程
首先说明一下，差分进化算法中，DE的群体由突变和选择过程驱动。突变过程，包括突变和交叉操作，这两步操作被设计用于利用或探索搜索空间，而选择过程被用于确保有希望的个体的信息可以进一步利用。

对于每一个个体来说，得到的解要好于或者持平于个体通过变异，交叉，选择达到全部最优。

基本差分进化算法的流程：

算法伪代码:

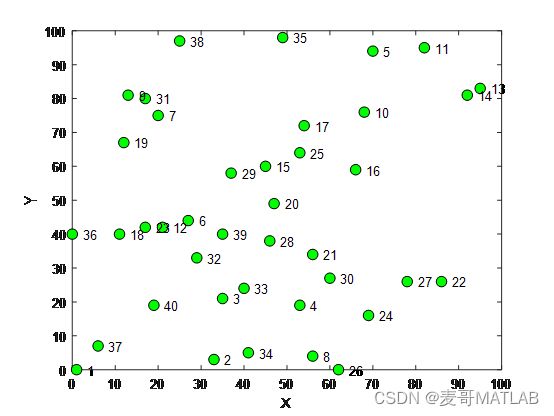
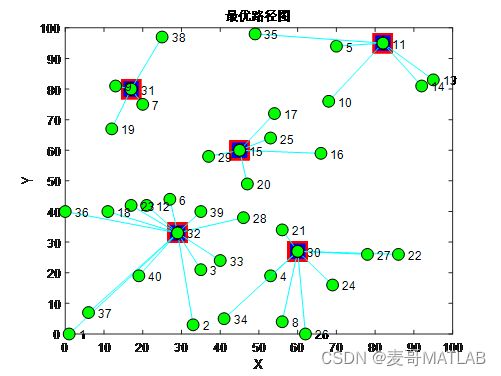
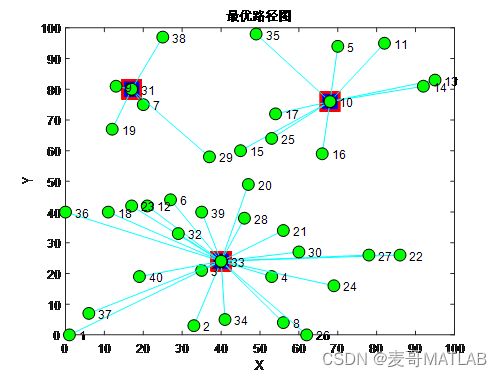
已知信息：40个超市的坐标位置图

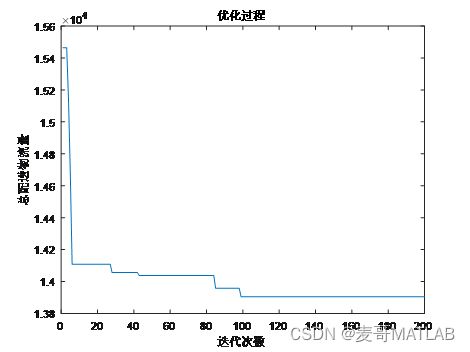
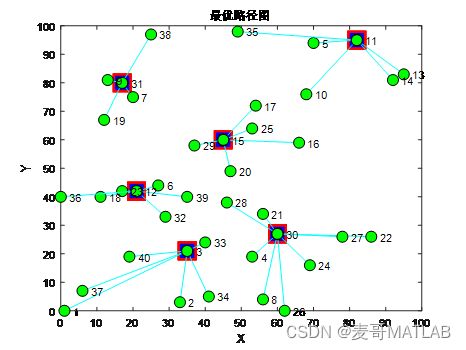
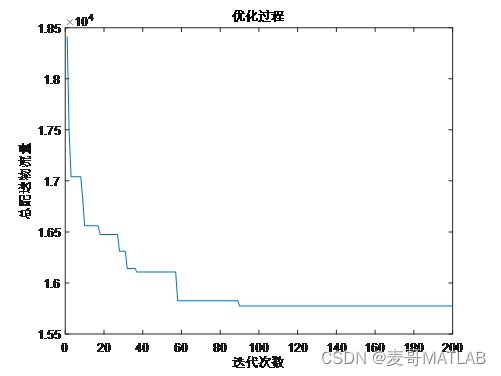
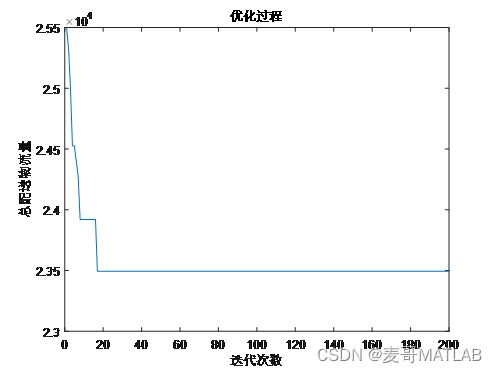
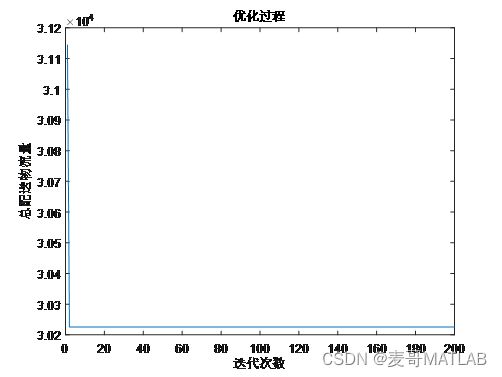
如何确定6个位置建立配送中心，使得6个配送中心到所有超市的总配送物流量（距离×需求量）最小呢？当然是通过算法优化求解啦！

先看下求解结果！
运行结果:
选择6个配送中心的运行结果：

最优解:
总配送物流量：13904.5804
选择5个配送中心的运行结果：

选择3个配送中心的运行结果：

选择2个配送中心的运行结果：