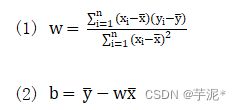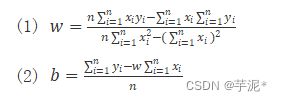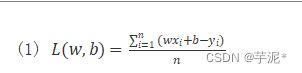【神经网路】tensorflow实验6--TensorFlow基础
目录
实验6
1. 实验目的
2. 实验内容
3. 实验过程
题目一:
题目二:
拓展题(选做):
4. 实验小结
实验6
1. 实验目的
掌握TensorFlow低阶API,能够运用TensorFlow处理数据以及对数据进行运算
2. 实验内容
①改变张量形状、维度变换和部分采样等
②张量加减乘除、幂指对数、多维向量乘法等运算
③使用TensorFlow求取张量在某个维度上或者全局的统计值
3. 实验过程
题目一:
使用TensorFlow张量运算计算w和b,并输出结果。
已知:
x=[ 64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03]
y=[ 62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84]
计算:
其中和分别为x和y的均值,是x中索引值为i的元素,是y中索引值为i的元素。
(3)分别输出w和b的结果。
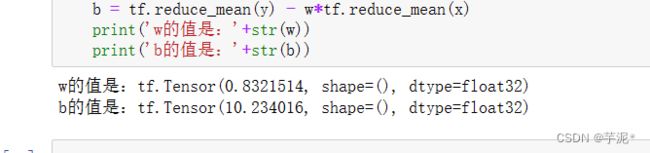
提示:正确的输出结果为w=0.83215 b=10.2340
① 代码
# x=[ 64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03]
# y=[ 62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84]
# 计算:
#
# 其中,xi是x中索引值为i的元素;yi是y中索引值为i的元素;n是张量中元素的个数。
# (3)分别输出W和b的结果。
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
x = (64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03)
y = (62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84)
x = tf.constant(x) #创建x张量
y = tf.constant(y) #创建y张量
def count_const():
sum1 = 0
sum2 = 0
for i in range(0, 10):
sum1 += (x[i] - tf.reduce_mean(x))*(y[i] - tf.reduce_mean(y))
sum2 += (x[i] - tf.reduce_mean(x))*(x[i] - tf.reduce_mean(x))
return sum1/sum2
if __name__ == '__main__':
x = (64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03)
y = (62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84)
x = tf.constant(x) # 创建x张量
y = tf.constant(y) # 创建y张量
w = count_const()
b = tf.reduce_mean(y) - w*tf.reduce_mean(x)
print('w的值是:'+str(w))
print('b的值是:'+str(b))② 实验结果
题目二:
使用TensorFlow张量运算计算w和b,并输出结果。
已知:
x=[ 64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03]
y=[ 62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84]
计算:
其中,xi是x中索引值为i的元素;yi是y中索引值为i的元素;n是张量中元素的个数。
(3)分别输出w和b的结果。
① 代码
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
if __name__ == '__main__':
x = (64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03)
y = (62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84)
x = tf.constant(x) # 创建x张量
y = tf.constant(y) # 创建y张量
n = int(tf.size(x)) # 求n的值
sum_xy = 0
sum_xx = 0
for i in range(10):
sum_xx += x[i]*x[i]
sum_xy += x[i]*y[i]
sum1 = (n*sum_xy)-(tf.reduce_sum(x)*tf.reduce_sum(y))
sum2 = (n*sum_xx)- (tf.reduce_sum(x)*tf.reduce_sum(x))
w = sum1/sum2
b = (tf.reduce_sum(y) - w*tf.reduce_sum(x))/n
print('w的值是:' + str(w))
print('b的值是:' + str(b))② 实验结果
拓展题(选做):
在题目二的基础上,已知x、y、w、b,计算L的值并输出结果。
其中,xi是x中索引值为i的元素;yi是y中索引值为i的元素;n是张量中元素的个数
(2)输出L的值
提示:
L= -9.918....e-06
① 代码
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
def count_L(w,b):
W_x = tf.multiply(w, x) # w*xi
W_x_b = tf.add(b, W_x) # w*xi+b
w_x_b_y = tf.subtract(W_x_b, y) # w*xi+b-yi
sum_l = tf.reduce_sum(w_x_b_y) # 求和w*xi+b-yi
sum_l = sum_l / n
return sum_l
if __name__ == '__main__':
x = (64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03)
y = (62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84)
x = tf.constant(x)
y = tf.constant(y)
n = int(tf.size(x)) #n的值
sum_x = tf.reduce_sum(x)
sum_y = tf.reduce_sum(y)
sum_x2 = tf.reduce_sum(x*x)
sum_xy = tf.reduce_sum(x*y)
w = ((n*sum_xy)-(sum_x*sum_y))/((n*sum_x2)-(sum_x*sum_x))
b = (sum_y-(w*sum_x))/n
print(count_L(w,b))② 实验结果
4. 实验小结
① 实验过程中遇到了哪些问题,你是如何解决的?
对张量计算中的函数运用不熟练,使得函数看起来很复杂,最后使用了张量计算函数之后是的函数简洁明了。
② TensorFlow和Numpy都可以对多维数组进行运算,他们各自的特点是什么?
相同点: 都提供n位数组
不同点: numpy支持ndarray,而Tensorflow里有tensor;
numpy不提供创建张量函数和求导,也不提供GPU支持。
③ 在题目基本要求的基础上,你对每个题目做了那些扩展和提升?或者你觉得在编程实现过程中,还有哪些地方可以进行优化?(可以从如何提高代码的简洁度来谈谈这个问题)
张量计算有着专门的函数,张量函数可以使得代码更简单,可以更加快速的得到想要的值。