机器学习3—分类算法之K邻近算法(KNN)
K邻近算法(KNN)
- 一、算法思想
- 二、KNN类KNeighborsClassifier的使用
- 三、KNN分析红酒类型
-
-
- 3.1红酒数据集
- 3.2红酒数据的读取
- 3.3将红酒的数据集拆分为训练和测试集
- 3.4KNN算法分析
-
- 总结
一、算法思想
KNN分类算法是最近邻算法,字面意思就是寻找最近邻居,由Cover和Hart在1968年提出,它简单直观易于实现。下面通过一个经典例子来讲解如何寻找邻居,选取多少个邻居。图中需要判断右边这个动物是鸭子、鸡还是鹅?这就涉及到了KNN算法的核心思想,判断与这个样本点相似的类别,再预测其所属类别。由于它走路和叫声像一只鸭子,所以右边的动物很可能是一只鸭子。
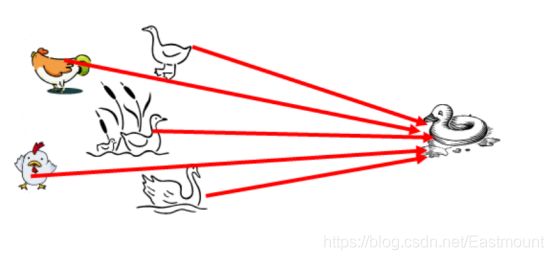
- KNN分类算法的核心思想是从训练样本中寻找所有训练样本X中与测试样本距离(常用欧氏距离)最近的前K个样本(作为相似度),再选择与待分类样本距离最小的K个样本作为X的K个最邻近,并检测这K个样本大部分属于哪一类样本,则认为这个测试样本类别属于这一类样本。
KNN分类的算法步骤如下:
- 计算测试样本点到所有样本点的欧式距离dist,然后采用勾股定理计算
- 设置参数K,并选择离带测点最近的K个点
- 从这K个点中,统计各个类型或类标的个数
- 选择出现频率最大的类标号作为未知样本的类标号,来反馈最终预测结果
对上述算法步骤举个例子:假设现在需要判断图中的圆形图案属于三角形还是正方形类别。
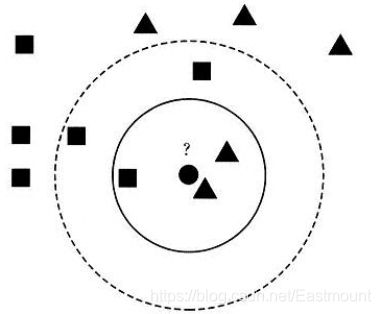
步骤:
- 当K=3时,图中第一个圈包含了3个图形,其中三角形2个,正方形一个,该圆的则分类结果为三角形。
- 当K=5时,第二个圈中包含了5个图形,三角形2个,正方形3个,则以3:2的投票结果预测圆为正方形类标。
- 同理,当K=11原理也是一样,设置不同的K值,可能预测得到结果也不同。所以,KNN是一个非常简单、易于理解实现的分类算法。
KNN算法的优缺点:
优点
- 简单易实现:KNN 算法最后实际 上并没有抽象出任何模型,而是把全部的数据集直接当作模型本身,当一条新数据来了之后跟数据集里 面的每一条数据进行对比。 所以可以看到 KNN 算法的一些优点,首当是这个算法简单,简单到都不需要进行什么训练了,只要把样本数据整理好了,就结束了,来一条新数据就可以进行预测了。
- 对于边界不规则的数据效果较好: 可以想到,我们最终的预测是把未知数据作为中心点,然后画一个 圈,使得圈里有 K 个数据,所以对于边界不规则的数据,要比线性的分类器效果更好。因为线性分类器可以理解成画一条线来分类,不规则的数据则很难找到一条线将其分成左右两边。
缺点
- 只适合小数据集: 由于算法太简单,所以每次预测新数据都需要使用全部的数据集,如果数据 集太大,就会消耗非常长的时间,占用非常大的存储空间。
- 数据不平衡效果不好: 如果数据集中的数据不平衡,有的类别数据特别多,有的类别数据特别少,那么这种方法就会失效了,因为特别多的数据最后在投票的时候会更有竞争优势。
- 必须要做数据标准化: 由于使用距离来进行计算,如果数据量纲不同,数值较大的字段影响就会变大, 所以需要对数据进行标准化,比如都转换到 0-1 的区间。
- 不适合特征维度太多的数据: 由于我们只能处理小数据集,如果数据的维度太多,那么样本在每个维度 上的分布就很少。比如我们只有三个样本,每个样本只有一个维度,这比每个样本有三个维度特征要明 显很多。
二、KNN类KNeighborsClassifier的使用
在Sklearn机器学习包中KNN分类算法的类是KNeighborsClassifier。构造方法如下:
KNeighborsClassifier(algorithm='ball_tree',
leaf_size=30,
metric='minkowski',
metric_params=None,
n_jobs=1,
n_neighbors=3,
p=2,
weights='uniform')
参数作用解析: 其中最重要的参数是n_neighbors=3,设置最近邻K值。和algorithm可以设置3种算法:brute、kd_tree、ball_tree。即 knn = KNeighborsClassifier(n_neighbors=3, algorithm=“ball_tree”)
-
algorithm :有 {‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选
快速k近邻搜索算法,默认参数为auto,可以理解为算法自己决定合适的搜索算法。除此之外,用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索,brute是蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时。kd_tree,构造kd树存储数据以便对其进行快速检索的树形数据结构,kd树也就是数据结构中的二叉树。以中值切分构造的树,每个结点是一个超矩形,在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的,其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体。 -
leaf_size : int,optional(默认值= 30)
默认是30,这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度,同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。 -
metric : 字符串或可调用,默认为’minkowski’
用于距离度量,默认度量是minkowski,也就是p=2的欧氏距离(欧几里德度量)。 -
met - ric_params : dict,optional(默认=None)
距离公式的其他关键参数,这个可以不管,使用默认的None即可。 -
n_jobs : int或None,可选(默认=None)
并行处理设置。默认为1,临近点搜索并行工作数。如果为-1,那么CPU的所有cores都用于并行工作。 -
n_neighbors : int,optional(default = 5)
默认情况下kneighbors查询使用的邻居数。就是KNN的k的值,选取最近的k个点。 -
p : 整数,可选(默认= 2)
距离度量公式。在上小结,我们使用欧氏距离公式进行距离度量。除此之外,还有其他的度量方法,例如曼哈顿距离。这个参数默认为2,也就是默认使用欧式距离公式进行距离度量。也可以设置为1,使用曼哈顿距离公式进行距离度量。 -
weights : str或callable,可选(默认=‘uniform’)
默认是uniform,参数可以是uniform、distance,也可以是用户自己定义的函数。uniform是均等的权重,就说所有的邻近点的权重都是相等的。distance是不均等的权重,距离近的点比距离远的点的影响大。用户自定义的函数,接收距离的数组,返回一组维数相同的权重。
KNN算法分析也包括训练和预测两个方法:
-
训练:knn.fit(data, target)
-
预测:pre = knn.predict(data)
举例操作一遍:
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
X = np.array([[-1,-1],[-2,-2],[1,2], [1,1],[-3,-4],[3,2]]) # 定义了一个二维数组用于存储6个点
Y = [0,0,1,1,0,1] # y坐标为负数的类标定义为0,y坐标为正数的类标定义为1(同理坐标x也一样)
Predict = [[4,5],[-4,-3],[2,6]] # 要预测的数据
knn = KNeighborsClassifier(n_neighbors=3, algorithm="ball_tree")
knn.fit(X,Y) # 训练模型
pre = knn.predict(Predict) # 预测[4,5]、[-4,-3]、[2,6]三个点的坐标
print('输出预测结果:')
print(pre)
# 计算K个最近点的下标和距离
distances, indices = knn.kneighbors(X)
print(indices) # 输出点的下标
print(distances) # 输出距离
输出为:
输出预测结果:
[1 0 1]
[[0 1 3]
[1 0 4]
[2 3 5]
[3 2 5]
[4 1 0]
[5 2 3]]
[[0. 1.41421356 2.82842712]
[0. 1.41421356 2.23606798]
[0. 1. 2. ]
[0. 1. 2.23606798]
[0. 2.23606798 3.60555128]
[0. 2. 2.23606798]]
三、KNN分析红酒类型
3.1红酒数据集
该实验数据集是UCI Machine Learning Repository开源网站提供的MostPopular Data Sets(hits since 2007)红酒数据集,它是对意大利同一地区生产的三种不同品种的酒,做大量分析所得出的数据。这些数据包括了三种类别的酒,酒中共13种不同成分的特征,共178行数据。
数据下载链接:https://archive.ics.uci.edu/ml/machine-learning-databases/wine/
该数据集包括了三种类型酒中13种不同成分的数量,13种成分分别是:Alcohol、Malicacid、Ash、Alcalinity of ash、Magnesium、Total phenols、Flavanoids、Nonflavanoid phenols、Proanthocyanins、Color intensity、Hue、OD280/OD315 of diluted wines和Proline,每一种成分可以看成一个特征,对应一个数据。三种类型的酒分别标记为“1”、“2”、“3”。数据集特征描述如下:

下载完后以.txt格式存储,其中每行数据代表一个样本,共178行数据,每行数据包含14列,即第一列为类标属性,后面依次是13列特征。其中第1类有59个样本,第2类有71个样本,第3类有48个样本。
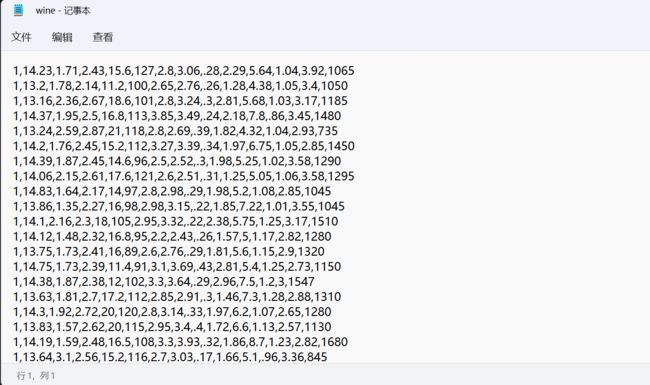
3.2红酒数据的读取
loadtxt()读入文件函数形式为:
loadtxt(fname, dtype, delimiter, converters, usecols)
其中参数fname表示文件路径,
dtype表示数据类型,
delimiter表示分隔符,
converters将数据列与转换函数进行映射的字段,如{1:fun},
usecols表示选取数据的列。
import os
import numpy as np
path = "wine.txt" # 存储wine.txt文件路径
data = np.loadtxt(path,dtype=float,delimiter=",") # 读取文件函数
data
输出为
array([[1.000e+00, 1.423e+01, 1.710e+00, ..., 1.040e+00, 3.920e+00,
1.065e+03],
[1.000e+00, 1.320e+01, 1.780e+00, ..., 1.050e+00, 3.400e+00,
1.050e+03],
[1.000e+00, 1.316e+01, 2.360e+00, ..., 1.030e+00, 3.170e+00,
1.185e+03],
...,
[3.000e+00, 1.327e+01, 4.280e+00, ..., 5.900e-01, 1.560e+00,
8.350e+02],
[3.000e+00, 1.317e+01, 2.590e+00, ..., 6.000e-01, 1.620e+00,
8.400e+02],
[3.000e+00, 1.413e+01, 4.100e+00, ..., 6.100e-01, 1.600e+00,
5.600e+02]])
3.3将红酒的数据集拆分为训练和测试集
由于Wine数据集前59个样本全是第1类,中间71个样本为第2类,最后48个样本是第3类,所以需要将数据集拆分成训练集和预测集。
步骤如下:
- 调用split()函数将数据集的第一列类标(Y数据)和上述13列特征(X数组)分隔开来。该函数参数包括data数据,分割位置,其中(1,)表示从第一列分割,axis为1表示水平分割(0表示垂直分割)。
- 由于数据集第一列存储的类标为1.0、2.0或3.0浮点型数据,需要将其转换为整型,这里在for循环中用int强制转化,存储至y数组中(也可采用np.astype()实现)。
- 最后调用np.concatenate()函数将0-40、60-100、140-160行数据分割为训练集,包括13列特征和类标,其余40-60、100-140、160-178行数据为测试集。
import os
import numpy as np
path = "wine.txt" # 存储wine.txt文件路径
data = np.loadtxt(path,dtype=float,delimiter=",") # 读取文件函数
# data
yy, x = np.split(data, (1,), axis=1) # yy=(178行数据,第一列类标)、x=(178行数据,13列特征)
print(yy.shape, x.shape)
y = []
# 将第一列数据转化为整型
for n in yy:
y.append(int(n))
train_data = np.concatenate((x[0:40,:], x[60:100,:], x[140:160,:]), axis = 0) #训练集
train_target = np.concatenate((y[0:40], y[60:100], y[140:160]), axis = 0) #样本类别
test_data = np.concatenate((x[40:60, :], x[100:140, :], x[160:,:]), axis = 0) #测试集
test_target = np.concatenate((y[40:60], y[100:140], y[160:]), axis = 0) #样本类别
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
输出结果:
(178, 1) (178, 13)
(100, 13) (100,)
(78, 13) (78,)
- 补充一种随机拆分的方式,调用 sklearn.model_selection.train_test_split 类随机划分训练集与测试集。
train_test_split(x, y, random_state=1, train_size=0.7)
参数x表示所要划分的样本特征集;
y是所要划分的样本结果;
train_size表示训练样本占比,0.7表示将数据集划分为70%的训练集、30%的测试集;
random_state是随机数的种子。
from sklearn.model_selection import train_test_split是在sklesrn库中导入model_selection类
3.4KNN算法分析
调用Sklearn机器学习包中KNeighborsClassifier算法进行分类分析,并绘制预测的散点图和背景图,代码如下:
import os
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
# from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
#第一步 加载数据集
path = "wine.txt"
data = np.loadtxt(path,dtype=float,delimiter=",")
#print(data)
#第二步 划分数据集
yy, x = np.split(data, (1,), axis=1) #第一列为类标yy,后面13列特征为x
print(yy.shape, x.shape)
y = []
for n in yy: # 将类标浮点型转化为整数
y.append(int(n))
x = x[:, :2] # 获取x前两列数据,方便绘图 对应x、y轴
train_data = np.concatenate((x[0:40,:], x[60:100,:], x[140:160,:]), axis = 0) # 训练集
train_target = np.concatenate((y[0:40], y[60:100], y[140:160]), axis = 0) # 样本类别
test_data = np.concatenate((x[40:60, :], x[100:140, :], x[160:,:]), axis = 0) # 测试集
test_target = np.concatenate((y[40:60], y[100:140], y[160:]), axis = 0) # 样本类别
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
# 第三步 KNN训练
clf = KNeighborsClassifier(n_neighbors=3,algorithm='kd_tree') # K=3
clf.fit(train_data,train_target) # 训练
result = clf.predict(test_data) # 预测
print(result)
# 第四步 评价算法
print(sum(result==test_target)) # 预测结果与真实结果比对
print(metrics.classification_report(test_target, result)) # 准确率precision 召回率 recall F值f1-score support
# 第五步 创建网格
x1_min, x1_max = test_data[:,0].min()-0.1, test_data[:,0].max()+0.1 # 第一列数据的最小值和最大值
x2_min, x2_max = test_data[:,1].min()-0.1, test_data[:,1].max()+0.1 # 第二列数据的最小值和最大值
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.1),
np.arange(x2_min, x2_max, 0.1)) # 生成网格型数据
print(xx.shape, yy.shape) # (53L, 36L) (53L, 36L)
z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # 将xx和yy矩阵都变成两个一维数组,调用np.c_[]函数组合成一个二维数组进行预测
print(xx.ravel().shape, yy.ravel().shape) # (1908L,) (1908L,)
print(np.c_[xx.ravel(), yy.ravel()].shape) # 合并 (1908L,2)
# 第六步 绘图可视化
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) # 颜色Map
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
plt.figure()
z = z.reshape(xx.shape) # 调用reshape()函数修改形状,将其Z转换为两个特征(长度和宽度)
print(xx.shape, yy.shape, z.shape, test_target.shape) # (53L, 36L) (53L, 36L) (53L, 36L) (78L,)
plt.pcolormesh(xx, yy, z, cmap=cmap_light) # 调用pcolormesh()函数来分类区域画图
plt.scatter(test_data[:,0], test_data[:,1], c=test_target,
cmap=cmap_bold, s=50) # x为test_data[:,0]\[:,1],y为test_target测试真实标签,s为设置大小
plt.show()
输出为:
(178, 1) (178, 13)
(100, 2) (100,)
(78, 2) (78,)
[1 3 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 3 2 2 3 2 2 2 2 2 3 2 2 2 2 2
2 1 2 2 2 3 3 3 2 2 2 2 3 2 3 1 1 2 3 3 3 3 3 1 3 3 3 3 3 3 3 1 3 2 1 1 3
3 3 1 3]
58
precision recall f1-score support
1 0.68 0.89 0.77 19
2 0.88 0.74 0.81 31
3 0.67 0.64 0.65 28
accuracy 0.74 78
macro avg 0.74 0.76 0.74 78
weighted avg 0.76 0.74 0.74 78
(53, 36) (53, 36)
(1908,) (1908,)
(1908, 2)
(53, 36) (53, 36) (53, 36) (78,)
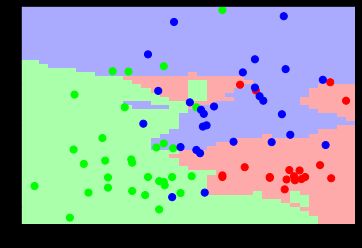
散点图中整个区域划分为三种颜色,左下角为绿色区域,右下角为红色区域,右上部分为蓝色区域。同时包括78个点分布,对应78行数据的类标,包括绿色、蓝色和红色的点。可以发现,相同颜色的点主要集中于该颜色区域,部分蓝色点划分至红色区域或绿色点划分至蓝色区域,则表示预测结果与实际结果不一致。
总结
最后对上述算法简单总结,整个分析过程包括六个步骤,大致内容如下:
-
- 加载数据集:
采用loadtxt()函数加载酒类数据集,采用逗号(,)来分割。
- 加载数据集:
-
- 划分数据集:
由于Wine数据集第一列为类标,后面13列为13个酒类特征,获取其中两列特征,并将其划分成特征数组和类标数组,调用concatenate()函数实现。
- 划分数据集:
-
- KNN训练:
调用Sklearn机器学习包中KNeighborsClassifier()函数训练,设置K值为3类,并调用clf.fit(train_data,train_target)训练模型,clf.predict(test_data)预测分类结果。
- KNN训练:
-
- 评价算法:
通过classification_report()函数计算该分类预测结果的准确率precision 召回率 recall F值f1-score support。
- 评价算法:
-
- 创建网格:
由于绘图中,拟将预测的类标划分为三个颜色区域,真实的分类结果以散点图形式呈现,故需要获取数据集中两列特征的最大值和最小值,并创建对应的矩阵网格,调用numpy扩展包的meshgrid()函数实现,在对其颜色进行预测。
- 创建网格:
-
- 绘图可视化:
设置不同类标的颜色,用pcolormesh()函数绘制背景区域颜色,再用scatter()函数绘制实际结果的散点图。
- 绘图可视化: