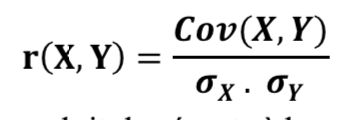统计学入门(零):协方差,皮尔逊系数及斯皮尔曼系数的R语言实现
前言:R语言是实践统计学和机器学习的良好工具,个人觉得相比Python比较容易学习。协方差,皮尔逊系数以及斯皮尔曼系数的具体统计学或数学意义就不在此过多描述,主要是解释其R语言代码实现,将分别使用公式的方式计算以及直接调用现有function的方式,以下是具体操作。
(一)首先导入数据并绘制图像,数据是介个样子:
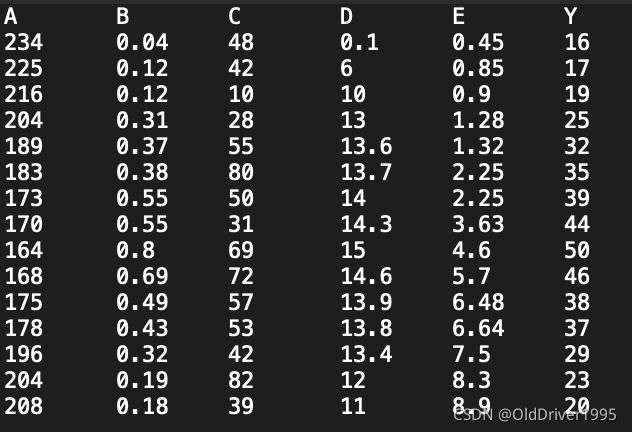
直接复制下面即可放到txt文本文件中就跟上面一样了,或者你也可以自己写数据,csdn这里的显示存在缩进问题,不用管他。
A B C D E Y
234 0.04 48 0.1 0.45 16
225 0.12 42 6 0.85 17
216 0.12 10 10 0.9 19
204 0.31 28 13 1.28 25
189 0.37 55 13.6 1.32 32
183 0.38 80 13.7 2.25 35
173 0.55 50 14 2.25 39
170 0.55 31 14.3 3.63 44
164 0.8 69 15 4.6 50
168 0.69 72 14.6 5.7 46
175 0.49 57 13.9 6.48 38
178 0.43 53 13.8 6.64 37
196 0.32 42 13.4 7.5 29
204 0.19 82 12 8.3 23
208 0.18 39 11 8.9 20
然后绘制数据,read.delim是导入数据的方式,然后par(mfrow(2,3))是为了图像显示时按照一个2行3列的方式展示,然后通过plot分别绘制A~E列和Y列的图表,data[1]或者data[,1]或者data[,c(1)]即为第一列,也就是A列,而data[1,]或者data[c(1),]则是第一行,但使用data[1]这种方式plot的时候会报错,所以还是老实用data[,1]或者data[,c(1)]吧。
##导入数据
data <- read.delim("~/Documents/CoursINFO4/Machine Learning/dataAnalysis/data1TP1.txt")
a<-data[,1]
b<-data[,2]
c<-data[,3]
d<-data[,4]
e<-data[,5]
y<-data[,6]
##(1)显示图像
par(mfrow=c(2,3)) #设置2行3列的分割
plot(a,y)
plot(b,y)
plot(c,y)
plot(d,y)
plot(e,y)
绘制完之后的图像如下图所示:
(二)然后是通过协方差和标准差获得皮尔逊系数,其公式如下:
#(2.1)计算皮尔逊相关系数
ro1 <- cov(a,y)/(sd(a)*sd(y))
ro2 <- cov(b,y)/(sd(b)*sd(y))
ro3 <- cov(c,y)/(sd(c)*sd(y))
ro4 <- cov(d,y)/(sd(d)*sd(y))
ro5 <- cov(e,y)/(sd(e)*sd(y))
可得到结果如图:
(三)调用函数进行验证:
#(2.2)用现成的函数验证
res1<-cor(a,y)
res2<-cor(b,y)
res3<-cor(c,y)
res4<-cor(d,y)
res5<-cor(e,y)
通过验证发现结果相等:
(五)接下来是斯皮尔曼相关系数,其公式如下:
这个R表示该元素在这一列中的排名,即Rank,R语言中可直接使用Rank函数。
# 斯皮尔曼系数
sro1<-1-6*sum((rank(a)-rank(y))^2)/(15^3-15)
sro2<-1-6*sum((rank(b)-rank(y))^2)/(15^3-15)
sro3<-1-6*sum((rank(c)-rank(y))^2)/(15^3-15)
sro4<-1-6*sum((rank(d)-rank(y))^2)/(15^3-15)
sro5<-1-6*sum((rank(e)-rank(y))^2)/(15^3-15)
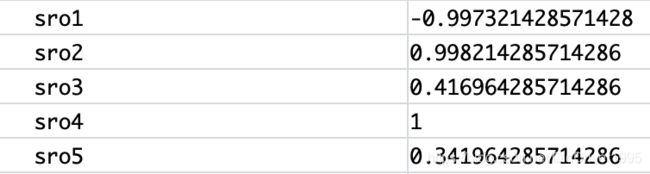
结果如下:
通过结果可以看出,对于第一个图,参数的负相关性较大,而第二组数据和第四组数据都是正相关性较大,3和5则是正相关性较小。和最开始画出来的图是相符的。
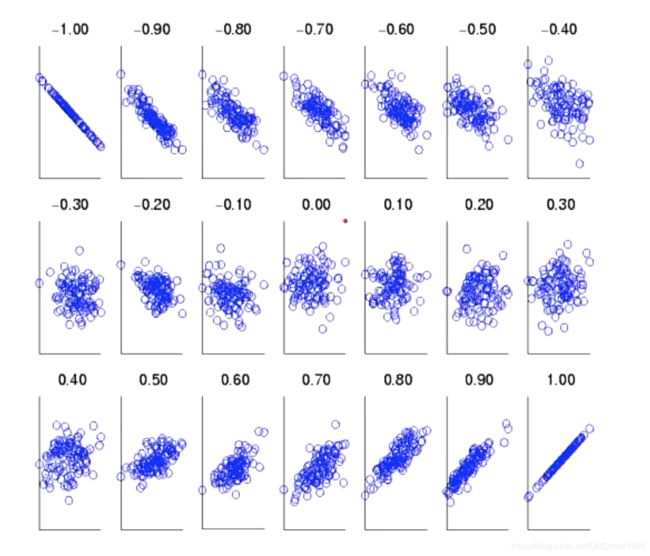
以下是一张用来直观体现从 -1 到 +1 的相关性的图:
(六)同样也可以通过公式直接获得,代码如下,但唯一遇到的问题是这两种方式的结果会存在千分位级别左右的差距:
## 验证
sp1<-cor(a,y,method="spearman")
sp2<-cor(b,y,method="spearman")
sp3<-cor(c,y,method="spearman")
sp4<-cor(d,y,method="spearman")
sp5<-cor(e,y,method="spearman")