机械臂路径规划path planning

一、路径规划：假设机械臂的终端结构要从一个点运动到另一个点，我们要求所有的关节和终端机构在运动的过程中都不能碰到障碍物，这个称为路径规划。

1、路径规划算法主要可分成两种：

（1）一种是基于搜索结果的规划（如A star算法）通常是运行在栅格地图上的。当栅格的分辨率越大时，算法搜索的路径就会越优。

（2）另一类是基于采样的规划。主要就是RRT以及它的各种变种算法(RRT*、RRTconnect等)，这也是机械臂最常用的路径规划算法。这类算法的核心在于随机采样，从父节点开始，随机在地图上生成子节点，连接父子节点并进行碰撞检测，若无碰撞，就扩展该子节点。

RRT是一种多维空间中高效的规划方法，它以一个初始点作为根节点，通过随机采样增加叶子节点的方式，生成一个随机扩展树。随机扩展树不断增长，直到到达目的位置。就这样，不断地随机扩展样本点，直到生成一条连接起点和终点的路径。

2、路径规划算法的还有一个划分的方式：

（1）全局路径规划：

基于环境全局的信息，这包含了机器人在当前状况下检测不到的所有信号。全局规划把环境信息存放到一幅图中，并利用这张图寻找可能的路线。由于全局算法通常要求花费大量的运算时间，因此不适合于高速多变的动态环境，并且由于全局路径规划必须要预先掌握全局的环境信息，也不适合于未知环境下的规划任务。

（2）局部路径规划：

只考虑了机器人的瞬时环境信号，使得计算数量减少，效率明显提高。但局部路径规划算法，有时并不一定可以让机器人直接抵达目的地点，从而导致了计算全局不收敛。

注意：对移动机器人来说，兼顾非完全微分约束的路径规划问题是该领域的难点所在。

3、机械臂应用RRT算法路径规划：

1.创建多维状态空间

2.构建joint space的障碍检测算法

3.在joint space应用RRT

4、路径规划算法--图搜索法

图搜索法通过利用已有的环境地图和版图中的障碍物等数据信息建立，由起点至结束点的可行路线。一般分为深度最优和广度最优二种走向。

-->深度优先算法：

优先拓展搜索深度较大的节点，因此能够更迅速的获得下一个可行路径，不过深度优先算法获取的第一个路径通常是比较长的路径。

-->广度优先算法：

优先拓展深入较小的节点，呈波形的检索方式。因此广度优先算法检索到的第一个路径通常是最短路径。

（1）可视图法：

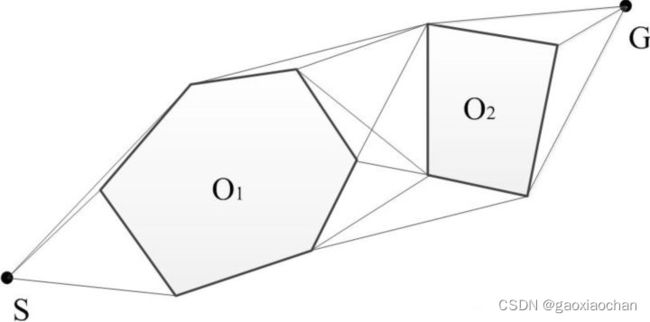
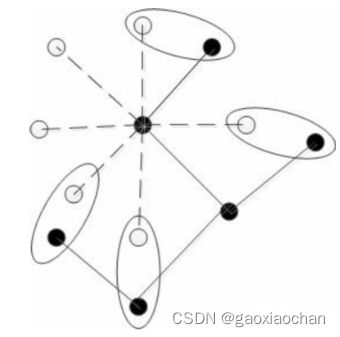
   可视图法是由Lozano-PErEz和WESlEy于1979年所创立的，是机器人全局运动计划中的典型算法。在视野法中，机器人用点来表示，阻碍物用多角形表示。把起始点S、目标点G，以及多角形阻碍物的所有顶点（设V零是各个阻碍物的顶端组成的整体）进行了综合联系，并规定起始点和阻碍物各顶部相互之间、目标点与阻碍物各顶部相互之间和各个阻碍物顶部和顶端相互之间的连接都不得通过阻碍物，即直线是"可视的"。给图中的所有边赋值，然后建立了可视地图G（V，E），并且点集V=∪{S，G}，E为每个弧段中即可视边的总和。然后釆用一些优化计算就找到了从开始点S到目标点G的最优预测路径，那么再经过累加并对比上述直线的距离就可以得出了从开始点到目标点的到V路径，如图所示。

    可视图法虽然能获得较短路线，但搜索时长过久，而且没有灵敏度，亦即一旦自动化机器人的起始点和目标地点都出现了变化，就需要重新建立可视图，相当困难。所以可视野法更适用于多边形障碍物，对圆障碍物则没有。

（2）Dijkstra算法

    Dijkstra计算由荷兰最著名的计算机物理学家艾兹赫尔.戴克斯特拉（Edsger Wybe Dijkstra）给出，通过预测从初始点至空间中任意一个点的最短距离，使其能够获取全局最佳路径。Dijkstra算法是一个典型的广度最大化的状态空间搜索算法，该算法能够从起始位置出发逐层一层的寻找整个自由空间，直至最后抵达目标地点。但是这会增加运算时间和数据量。而另一方面，依靠搜索而得到的大量数据对于机器人驾驶者来说又是毫无意义的。

   初始化时，每个经过原点s的路径权重均被赋为0（dis[s]=0）。假定在一个顶角s有可以径直到达的所有边（s，m），则把dis[m]设为w（s，m），并且把任何任何（s无法径直抵达的）边的路径宽度均定为无穷大。在起始时间，集合T中存在顶角s。

   然后，如果在dis数组选取最低位，那么这个数值就是在源点s和该值所相应的顶点之间的最短路线，同时将该点加入到T中，就OK了，此时就是一个顶点的完成。

   接着，要查看自己新增加的节点是不是能够抵达其他节点，并且看看使用这个节点抵达其他点的路线距离是不是比从源点直接抵达还要短，要是有，那就需要更换这个节点在dis上的位置。

   接着，再在dis中寻找最小值，并重复以上动作，直至T中包含出图的全部顶点。

（3）A star算法

   A Star计算作为一种启发式计算被引入。该计算在广度优先的基石上增加了一种估价函数。Astar计算的核心问题就在估价函数的设计上，如下式所示: F(n)=g(n)+h(n)

  其中g(n)为时间耗散函式，代表了从开始结点n start到终止节点n的真实代价；H(n)又称启发函数，指示节点n到目标节点n goal的估算价格；f(n)则指出由初始化节点经由目的节点n至目标节点的估算价格付出代价。和Dijkstra计算相似，Astar计算也维持了一个Open列表。在Open表中节点的优先权是按照f(n)的多少来排序的，f(n)值越小，被检索到的优先权也就越高。

   为了确保能获得最佳值，启发函数的h(n)不宜太大，不宜超过节点n到目标节点的现实付出代价一旦h(n)=0，则可使A star计算退化成Dijkstra计算，尽管其能提供最佳途径，但计算效率却依然较差；假设h(n)值正好小于节点n到目标节点的现实付出代价，则A star计算所寻找的目标结点就正好是在最优预测路线上的目标节点。所以h(n)的取值影响计算的速率和准确性。

 5、路径规划算法--快速搜寻随机树算法

   快速搜寻随机树（RRT）算法是一个增量式采样的搜寻技术，这个算法在实际使用中并不要求将任何参数整定，因此具有极好的使用性能。在极端环境情况下，该搜寻树将稠密的充满全部空间，此时搜寻树由许多较小曲线或路经组成，以达到填满全部空间的目的。

   增量式运算中，所建立的速率搜寻树其方向通常都是稠密采样次序，但一旦该顺序是绝对随意的时，那么这种速率搜寻树就叫做速度搜寻绝对随机树（Rapidly Exploring Random Tree，RRT），而不管该次序为绝对随意的或是确定性次序，都被称之为速率搜寻稠密树（Rapidly Exploring Dense Trees，RDTs）

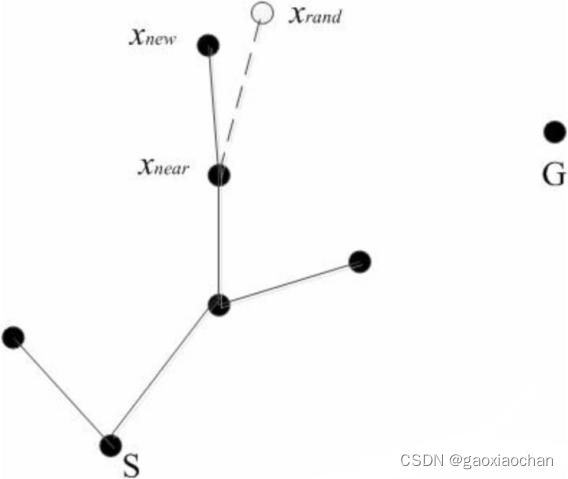
    基本步骤：先从自由空间中随机选择下一个新的状态结点X rand，然后再以遍历当前的速度随机寻找新状态树T，并寻找在T上离X rand最近的新状态结点X near，朝着X near的方向生长，如果没有碰到障碍物就把生长后的树枝和端点添加到树上记为X new。完成搜索树构造之后，再从目标节点入手，逐渐查找父节点直至达到初始状态，即开始查找下一棵树的根结点。

 （2）改进算法

   在采集策略方面，RRTGoalBiaS方式在监控机器人随机运动的时候，也以特定几率向最终目标运动；而RRTGoalZoom方式则需要从整体空域，以及在目标地点附近的小空域中完成采集；RRTCon方法则由于增加随机步长提高了计划速率。

   ①基本RRT方法：在收敛到终点位置上运行的速率稍许缓慢。为进一步提高计算的质量与稳定性，应进一步对方法加以完善。如进一步提高搜寻工作效率，引入了双向随机搜索树（Bi~RRT），在初始节点上与目标节点之间并行产生二棵RRT，直到最后二棵树相遇，计算才收敛。这个算法相对于RRT树而言有较高的收敛性，而且对于目前路径规划算法中是较为普遍的。

    ②RRT-connect算法：是基于RRT算法的一种算法，在RRT的基础上引入了双树扩展环节，分别以起点和目标点为根节点生成两棵树进行双向扩展，效率会更高。当两棵树建立连接时可认为路径规划成功。通过一次采样得到一个采样点X rand ，然后两棵搜索树同时向采样点X rand​方向进行扩展，加快两棵树建立连接的速度。相较于单树扩展的RRT算法，RRT-Connect加入了启发式步骤，加快了搜索速度，对于狭窄通道也具有较好的效果。

RRT-connect算法每次选择较小的那棵树进行拓展，搜索速度、搜索效率有了显著提高。但是RRT-Connect和RRT一样，都是单查询算法，最终路径并不是最优的。

   ③双向RRT*算法：是基于随机采样的渐近最优路径规划算法。改进了原有RRT算法的父节点选择方式，选取路径代价函数最小代价的节点为父节点，同时，每次选择父节点之后会重新连接所有节点，进而计算出路径的渐进最优解。RRT*算法的核心有两个过程：重新选择父节点和重布线随机数。

重新选择父节点：定义新节点X new 的搜索半径范围，在新产生的节点X new 的该范围内搜索附近的节点，作为替换X new 父节点的备选。首先，计算起点到附近节点的路径代价，然后加上X new 到附近节点的路径代价。

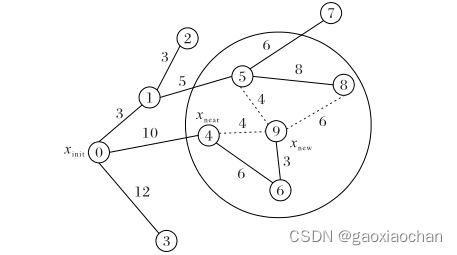
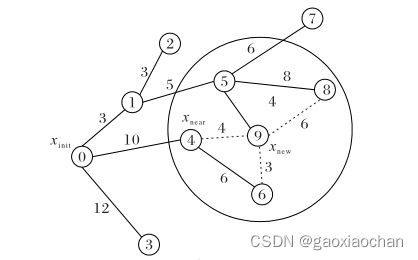
节点标号代表该节点产生的顺序，节点9是节点6新产生的节点X new ，两个节点之间连线上的数字即为两个节点之间的欧氏距离。重选父节点时，以节点 9的X new 为圆心，按照定义的半径范围，找到该范围内X new 附近的节点，即节点4、5、8。原来的路径0-4-6-9代价为19，该节点附近备选的三个节点与X new 组成的路径0-1-5-9、0-4-9和0-1-8-9代价分别为12、14和22，因此，在附近的节点中，节点5的路径代价相对最小，将节点5变为节点9的父节点，则重新生成的随机树为下图Ⅱ所示。

Ⅰ生成随机点过程：

Ⅱ重选父节点过程：

 重布线随机数：在为X new 重新选择父节点之后，为随机树进行重布线。如下图所示，重布线的具体过程为：如果附近节点的父节点改为X new ，可以减小路径代价，则更改该节点的父节点。如图Ⅰ所示，节点9为新生成的节点X new ，近邻节点分别为节点4、6、8，它们的父节点分别为节点0、4、5，路径分别为0-4、0-4-6、0-1-5-8，代价分别为10、16和16。如果将节点4的父节点改为节点9，其路径也发生变化，该路径的代价为16，大于原来的路径代价10，因此保持节点4的原来父节点不变。同理，也保持节点8的父节点不变。如果改变节点6的父节点为X new ，该路径的代价变为15，小于原来的路径代价16，因此将节点9作为节点6的父节点，改变之后新随机树如图Ⅱ所示。从整体的路径代价来看，每当生成了新的节点后，通过重新布线使得某些节点的路径代价减少，每一次的重布线都有机会减小最终的路径代价。

Ⅰ生成随机点过程：

 Ⅱ重布线随机树过程：

6、滚动规划

基本步骤：

第一步为0:先对起始、终端、环境、机器人的视线半径、步长等完成初始化；

步骤1:若终点抵达，则规划中止；

操作2:对当前滚动窗内的所有环境消息予以刷新；

步骤3:产生局部子目标；

过程4:基于子目标和现存条件信息，在当前滚动窗口内计划一个经过调整的局部有效路线；

方法5:按规划的局部路径走进每一步，步长必须等于视野半径；

步骤6:返回步骤1。

滚动在线RRT算法：在一个滚动窗口内，随机树以当前区域为开始节点，并建立传感器区域内的所有随机树。结构方式与最基本RRT算法相同。

但能够使在全局条件中随机树产生朝目标方向发展的态势，在运动规划时导入启发信号，以降低随机树的随机性，并增加搜索效果

以Road（x1，x2）指代随意树中二个位置节点间的道路价格，Dis（x1，x2）指代随意树中二个位置节点间的欧几里德距离。相似于Astar方法，本方法为随意树中各个节点设定一种估值参数:f（x）=g（x）+h（x）。当中g（x）=Road（x，X rand）为随意节点，而X rand则代表到树中目的结点x所需的道路时间。H（x）是启发的估值参数，在此处可取随意节点X rand到目标节点X goal的距离作为估计值，h（x）=Dis（X rand，X goal）。f（x）就代表了从目的节点x经随机结点X rand至目的地节点xgoal的路线估量值。遍历滚动窗内随机树T时，若取估量函数中较小值的结点X near，则f（X near）=min（f（x））。

 具体方法：

（1）对滚动窗口随机树T初始化后，T起始时只包括了起始地址S；

（2）滚动窗口自由空间中，随机选取了一种状态的xrand；

（3）基于最短路线的思想寻找在树T中，与xrand距离最近的结点xnear；

（4）选择输入u，将机器人状态由xnear到xnew；

（5）确定了xnew是否满足回归分析，不满足则返回第四步骤；

（6）将xnew看作随机树T的一个新结点时，u将被写在连接结点xnear的xnew的边上。

 7、BUG1算法

基本思路：在目标周围毫无阻挡物体时，顺着垂直路径朝目标运动即可获得最短的路径。当感应器侦测到了车辆时，自己绕行车辆直到还能持续围绕着直线项目标运动。

   假设机器人能够测定二点之间的相对位移，但不考虑自动化机器人的相对位移偏差。初始地点和当前位置分别以q start和q goal表示；而机器人在i时的相对位置则显示为xi；L代表了联系着自己所在地xi和当前地点的直线。

   在开始时，xi=q start。如果还不能探测到障碍物，那么机器人将沿着l向目标方位直行，直到抵达当前地点并碰到障碍物。在碰到障碍物后，将记下当前地点qHi。

   接着机器人将周绕所有障碍物直到最后一次到达qHi，然后将寻找环绕路线中距离目标最近的下一地点qLi，并沿着障碍物边缘移动至当前地点。

   然后，将直线l改变，机器人继续沿着直线朝目的地方位前进。但是如果在这条直线的途中仍然会出现该障碍物，则机器人将始终不能抵达目标地点。否则算法将会不断的循环直至机器人再次抵达目标地点，又或者计算机依旧认为机器人还没能到达目标地点。

 8、BUG2算法

   BUG二算法中，也有另外二个运动：沿着目标的方向直行，还是沿着边界方向绕行。不过和BUG1计算结果不同的是，在BUG2计算结果中的直线l是联系在起始点与目标点之间的直线，在整个计算流程中保持速度恒定。

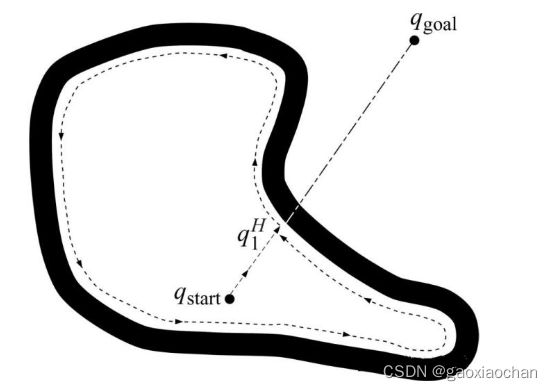
   当机器人所在地点附近出现障碍物时，机器人就开始绕道障碍物，但如果机器人在绕道过程中在离目标更近的地方上再次出现了垂直l，那么就终止了绕道，转而仍然顺着垂直l朝目标方向直行。进行了这样的恶性循环，直到机器人抵达了目标地q goal。

   但假如机器人在绕道过程中并不是出现在直线L上，与目标地点距离更接近的qLi地点，而是直接到达了qHi地点，则得出的结论，就是机器人并不能到达目标。如图所示。

   BUG1和BUG2计算都提供了查找问题的二个基本方式：较为保守的BUG1计算采用了更加精细的方式寻找，来获得最佳的距离地点。这就要求机器人围绕着各个障碍物的边界。而BUG2计算则选取了一种比较投机的方法。面对较为普通的环境，BUG2计算的效能将会较高；但面对较复杂类型的障碍物，在相对保守的环境BUG1计算性能将更好。

 二、轨迹规划

    如果我们规定从A到B这个path，必须在特定的时间 (t0 -t6)，经过这7个点。那么这7个点叫waypoints。轨迹 (traiectory) 指的是通过这7个点的具体计划(例如什么时间，以什么速度等等)。规划我们如何经过这7个点的算法，叫做轨迹规划（trajectory planning）算法。

角度空间：在waypoints调用逆运动学，然后在角度空间插值

任务空间：在任务空间插值，每一步调用逆运动学

三、运动规划

   可以认为是更加宽泛的概念，它规划的结果是让机器人实现某种约束目标的动作(motion)，这些动作既可以是离散的空间路径点。r1,r2,...,rn，也可以是一个连续的空间路径 r(8)，又可以是带有时间信息的空间轨迹 r(t)，其至可以是机器人底层的控制信息 u(t)或者是某种控制策略。

路径规划和轨迹规划统称为运动规划。