【数据结构与算法】第一篇：栈，队列

---

一.栈（Stack）

1.栈的特性

栈是一种特殊的线性表只能在一端进行操作。
1.往栈中添加元素的操作，叫做入栈（push）
2.从栈中移除元素的操作，一般叫做 pop，出栈（只能移除栈顶元素，也叫做：弹出栈顶元素）
3.栈遵循先进后出的原则，这一点和队列有着本质区别，要注意区分！

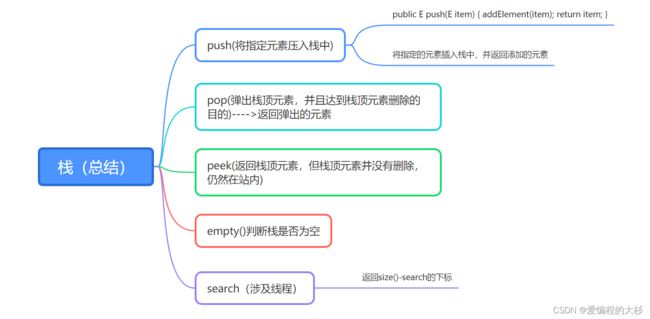
2.栈的接口设计

接口设计

◼ int size(); // 元素的数量
◼ boolean isEmpty(); // 是否为空
◼ void push(E element); // 入栈
◼ E pop(); // 出栈
◼ E top(); // 获取栈顶元素
◼ void clear(); // 清空

源码分析

public
class Stack<E> extends Vector<E> {
    /**
     * Creates an empty Stack.
     */
    public Stack() {
    }

 
    public E push(E item) {
        addElement(item);

        return item;
    }
    public synchronized E pop() {
        E       obj;
        int     len = size();

        obj = peek();
        removeElementAt(len - 1);

        return obj;
    }
    public synchronized E peek() {
        int     len = size();

        if (len == 0)
            throw new EmptyStackException();
        return elementAt(len - 1);
    }

    public boolean empty() {
        return size() == 0;
    }

  
    public synchronized int search(Object o) {
        int i = lastIndexOf(o);

        if (i >= 0) {
            return size() - i;
        }
        return -1;
    }

    /** use serialVersionUID from JDK 1.0.2 for interoperability */
    private static final long serialVersionUID = 1224463164541339165L;
}

源码个方法的功能分析
✔✔注意pop与peek的区别！！

3.用动态数组实现栈

package com;

import java.util.ArrayList;

public class Stack <E>{
//调用java本身的ArrayList(顺序表)
    ArrayList<E> list = new ArrayList<>();

    public void clear() {
    //清空栈=清空数组。栈有这个操作也是很合理的
        list.clear();
    }
//栈中元素的数量=数组中元素数量
    public int size() {
    return  list.size();
    }
    public boolean isEmpty() {
    return list.size()==0;
    }
    public void push(E element) {
        list.add(element);
    }
    public E pop() {
//因为栈是后进先出，所以从数组的尾部开始删除
        return  list.remove(list.size()-1);
    }

//获得栈顶元素
    public E top() {
    return list.get(list.size()-1);
    }
}

4.leetcode练习：有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。 

提示：

1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成

具体题意请点击这里哈✔✔✔✔✔

（1）题目解析：

（2）代码实现

class Solution {
    public boolean isValid(String s) {
    Stack<Character> stack=new Stack<>();
    for(int i=0;i<s.length();i++){
        char c=s.charAt(i);
        if(c=='('||c=='['||c=='{')
        {
                stack.push(c);
        }
        else{
            if(stack.isEmpty())
            {
                return false;
            }
        char left=stack.pop();
        if(left=='('&&c!=')')return false;
        if(left=='['&&c!=']')return false;
        if(left=='{'&&c!='}')return false;
        }
            }
            return stack.isEmpty();
        }
}

二.队列（Queue)

1.队列基础认知

◼ 队列是一种特殊的线性表，只能在头尾两端进行操作
◼队尾（rear）：只能从队尾添加元素，一般叫做 enQueue，入队
◼队头（front）：只能从队头移除元素，一般叫做 deQueue，出队
◼先进先出的原(与栈相反)

2.用链表实现初级队列（单端非循环队列）

（1）接口设计+源码

接口设计

◼ int size(); // 元素的数量
◼ boolean isEmpty(); // 是否为空
◼ void clear(); // 清空
◼ void enQueue(E element); // 入队
◼ E deQueue(); // 出队
◼ E front(); // 获取队列的头元素

源码框架

（2）用链表实现队列

public class Queue<E> {
    List<E> list=new LinkedList<>();
    public int size(){
        return list.size();
    }
    public boolean isEmpty(){
        return list.isEmpty();
        //方法二：return list.size()==0
    }
    public void clear(){
        list.clear();
    }
    public void enQueue(E element){
    list.add(element);
    }
    public E deQueue(){
    return list.remove(0);
    }
    public E front(){
        return list.get(0);
    }


}

3.单端循环队列

循环队列本质也是动态数组实现的
他主要解决以下空间利用与特殊需求的问题：如图

public class CircleQueue<E> {
    private int front;
    private int size;
    private E[] elements;
    private static final int DEFAULT_CAPACITY = 10;

    public CircleQueue() {
       elements=(E[])new java.lang.Object[DEFAULT_CAPACITY];
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    private int index(int index)
    {
        index=front+index;
        return index-(index>elements.length? elements.length:0);
    }
    public void clear() {
        for (int i = 0; i <size ; i++) {
            elements[index(i)]=null;
        }
        front=0;
        size=0;
    }

    public void enQueue(E element) {
    ensureCapacity(size+1);
    elements[index(size)]=element;
    size++;
    }

    public E deQueue() {
    E fontElement=elements[front];
    elements[front]=null;
    front=index(1);
    size--;
    return fontElement;
    }

    public E front() {
      return elements[front];
    }

    @Override
    public String toString() {
        StringBuilder str=new StringBuilder();
        str.append("size=").append(size).append(" ").append("front=").append(front);
        str.append("[");
        for (int i = 0; i <elements.length ; i++) {
            if(i!=0)
            {
                str.append(",");
            }
            str.append(elements[i]);

        }
//        for (int i = front; i 
//            str.append(elements[(i+front)%elements.length]).append(" ");
//        }
        str.append("]");
        return str.toString();
    }


    /**
     * 保证要有capacity的容量
     * @param capacity
     */
    private void ensureCapacity(int capacity) {
        int oldCapacity=elements.length;
        if(oldCapacity>capacity)
        {
            return;
        }
        int newCapacity=oldCapacity+oldCapacity>>1;
       E[] elem=(E[])new Object[newCapacity];
        for (int i = 0; i <oldCapacity ; i++) {
            elem[i]=elements[index(i)];
        }
        elements=elem;
        front=0;
    }
}

4.双端队列

（1）接口设计

注意：和单端对列不同的两处 1.是从对头入队
2.是从对尾出队（链表可以很好的解决这两个问题）

public class MyDeque <E>{
    List<E>list=new LinkedList<>();
    // 元素的数量
    public int size(){
        return list.size();
    }
    public boolean isEmpty(){

        return list.isEmpty();
    }
    public void clear(){
        list.clear();
    }
    // 从队尾入队
    public void enQueueRear(E element){
    list.add(element);
    }
   public E deQueueFront(){
     return list.remove(0);
   }
   public  void enQueueFront(E element){
        list.add(0,element);
   }
    public E deQueueRear(){

       return list.remove(list.size()-1);
    }
    // 获取队列的头元素
     public E front(){
         return list.get(0);
     }
      public E rear(){
        return list.get(list.size()-1);
      }

}

5.双端循环队列

@SuppressWarnings("unchecked")
public class CircleDeque<E> {
    private int front;
    private int size;
    private E[] elements;
    private static final int DEFAULT_CAPACITY = 10;

    public CircleDeque() {
        //默认初始化容量为10
        elements = (E[])new Object[DEFAULT_CAPACITY];
    }

    public int size(){
        return size;
    }
    public boolean isEmpty(){

        return size==0;
    }
    public void clear(){
        //清除所有对象，并将对列重置
        for (int i = 0; i <size ; i++) {
            elements[index(i)]=null;
        }
        front=0;
        size=0;
    }
    private void ensureCapacity(int capacity) {
        int oldCapacity=elements.length;
        if(oldCapacity>=capacity)
        {
            return;
        }
        int newCapacity=oldCapacity+oldCapacity>>1;
        E[] elem=(E[])new Object[newCapacity];
        for (int i = 0; i <elements.length ; i++) {
            elem[i]=elements[index(i)];
        }
        //扩容的同时将队列重置
        elements=elem;
        front=0;
    }
    // 从队尾入队
    public void enQueueRear(E element){
        ensureCapacity(size+1);
        elements[index(size)]=element;
        size++;
    }
    private int index(int n)
    {

        if (n<0)
        {
            //n=-1的情况
            return n+elements.length;
        }
        else {
            n=n+front;
            //特殊情况：front=0的时候
            return n-(n>elements.length?elements.length:0);
        }
    }
    public E deQueueFront(){
        E oldElement=elements[front];
        elements[front]=null;
        front=index(1);
        size--;
        return oldElement;
    }
    //从对头进
    public  void enQueueFront(E element){
        ensureCapacity(size+1);
        front=index(-1);
        elements[front]=element;
        size++;
    }
    //从队尾出
    public E deQueueRear(){

        int oldDate=index(size-1);
        E rearElement=elements[oldDate];
        elements[oldDate]=null;
        size--;
        return rearElement;
    }
    // 获取队列的头元素
    public E front(){
       return elements[front];
    }
    public E rear(){
        return elements[index(size-1)];
    }

}

三.leetcode:用栈实现对列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：

MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

方法：双栈轮换（辅助栈）
栈和队列的本质区别是1.栈->单端操作，对列->双端操作
2.栈是先入后出，队列是先入先出

模拟先进先出
这里要考虑如果outStack()栈里面本身就有元素的情况，则直接将outStack()栈里的元素弹出

代码实现

class MyQueue {

        Stack<Integer> inStack;
        Stack<Integer> outStack;
        public MyQueue() {
        //初始化双栈
        inStack=new Stack<>();
        outStack=new Stack<>();
        }

        /*入队（都放入inStack栈中）*/
        public void push(int x) {
            inStack.push(x);
        }

        private void check()
        {
            if (outStack.isEmpty()){
                while (!inStack.isEmpty()){
                    outStack.push(inStack.pop());
                }
            }
        }
        //出队
        public int pop() {
        //出栈如果inStack（）不为空，outStack（)为空。则直接将inStack()中的元素全部弹出到outStack(），再有outStack（）弹出
            check();
            return outStack.pop();
        }

        /*获取队头元素*/
        public int peek() {
            check();
            return outStack.peek();
        }

        public boolean empty() {
            return inStack.isEmpty()&&outStack.isEmpty();
        }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

四.leetcode:用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：

MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

1 <= x <= 9
最多调用100 次 push、pop、top 和 empty
每次调用 pop 和 top 都保证栈不为空

class MyStack {

    Queue <Integer> queue1;
     Queue <Integer> queue2;
    public MyStack() {
        queue1=new LinkedList<Integer>();
        queue2=new LinkedList<Integer>();
    }
    public void push(int x) {
        queue2.offer(x);
        while(!queue1.isEmpty())
        {
            queue2.offer(queue1.poll());

        }
    Queue<Integer> temp=queue1;
    queue1=queue2;
    queue2=temp;

    }
    
    public int pop() {
        return queue1.poll();
    }
    
    public int top() {
      return queue1.peek();
    }
    
    public boolean empty() {
       return queue1.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */