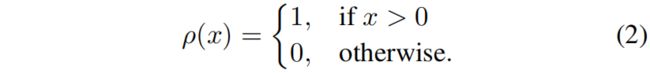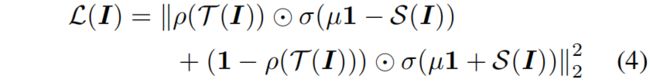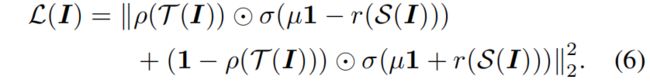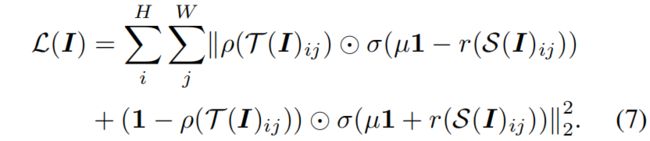Activation Boundaries（AAAI 2019）原理与代码解析

paper：Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons

official implementaion：https://github.com/bhheo/AB_distillation

Third party implementation：https://github.com/HobbitLong/RepDistiller/blob/master/distiller_zoo/AB.py

本文的创新点

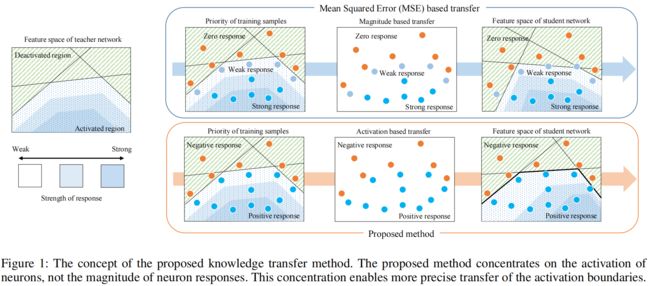
激活边界activation boundary是一个分隔超平面，它决定了神经元是激活的还是失活的。有研究指出，神经网络表示了一个由激活边界组合成的复杂函数。还有研究指出神经网络的决策边界是由激活边界组合而成的。这些研究表明将教师模型中的激活边界信息传递给学生模型对于分类模型的提升会有很大的帮助，这是因为分类问题在很大程度上依赖于类间决策边界。

基于此，本文提出了一种聚焦于传递激活边界的知识蒸馏方法。和传统的只关注神经元响应大小的方法不同，本文提出的方法旨在传递神经元是否激活的知识。

方法介绍

知识蒸馏有两种方法，一种是在学生模型训练的过程中传递知识，将传统的交叉熵损失和蒸馏损失结合起来形成一个单一的损失用于整个训练过程。另一种是用传递的知识初始化学生模型，然后基于交叉熵损失对模型进行分类训练。本文讨论的方法基于第二种。

教师网络从输入到某一隐含层定义为函数 \(\mathcal{T}\)，学生网络从输入到对应的隐含层定义为 \(\mathcal{S}\)。对于输入图片 \(I\)，教师网络隐含层的神经元响应向量为 \(\mathcal{T}(I)\in \mathbb{R}^{M}\)，学生网络为 \(\mathcal{S}(I)\in \mathbb{R}^{N}\)，其中 \(M\) 是隐含层的神经元个数。为了方便这里假设教师网络和学生网络对应隐含层的大小相同。为了描述神经元的激活情况，\(\mathcal{T}(I)\) 和 \(\mathcal{S}(I)\) 定义为激活函数之前的值。这里考虑ReLU \(\sigma (x)=max(0,x)\) 作为激活函数。现有方法如Fitnets中的神经元响应传递如下

它是ReLU激活函数后神经元响应之间的均方误差，这仅仅是让学生模型去近似教师模型的神经元响应，但由此产生的激活边界可能会有很大的不同。均方误差是一种偏向于较大差异的损失，因此这将主要转移具有强响应strong response的样本。但如图(1)所示，激活边界处于弱响应和零响应之间，因此基于式(1)的方法很难传递激活边界。

为了准确地传递激活边界，作者的想法是放大激活边界附近区域的可忽略的传递损失，为此定义了一个activation indicator function用来表示一个神经元是否是激活的

然后用来传递激活边界的损失如下

当教师和学生的激活状态不同时，该损失给出一个常量的惩罚。

但是由于 \(\rho()\) 是一个离散函数，activation transfer loss无法通过梯度下降来优化，因此作者提出了一种可以用梯度下降进行优化的替代损失函数。最小化激活传递损失类似于学习一个二分类的分类器，教师模型的神经元激活 \(\rho(\mathcal{T}(I))\) 等价于类别标签。如果教师的神经元是activated的，学生的神经元响应应该大于0，反之如果教师的神经元是deactivated，学生神经元的响应应该小于0。受这种启发，设计的替代损失函数类似于SVM中的hinge loss

其中 \(\odot \) 是向量间的element-wise product，\(1\) 表示一个长度为 \(M\) 所有值都为1的向量。替代损失给予学生模型中和教师激活状态不同的神经元一个平方的惩罚，而不关心具有相同激活的神经元。此外为了训练的稳定引入了一个边界 \(\mu\)。

Number of neurons

前面讨论的情况都是教师模型和学生模型神经元个数相同的情况，当神经元个数不同时，比如教师的神经元个数为 \(M(\mathcal{T}(I)\in \mathbb{R}^{M})\)，学生的神经元个数为 \(N(\mathcal{S}(I)\in \mathbb{R}^{N})\)，需要一个connector函数 \(r:\mathbb{R}^{N}\rightarrow\mathbb{R}^{M}\) 将学生模型的神经元响应向量转换为教师模型神经元响应向量的大小。使用connector function，式(4)变为下式

通常connector函数是一个全连接层或一个全连接层加一个BN层。在初始化过程中，connector function和学生网络 \(S\) 同时训练来最小化式(6)，在knowledge transfer初始化后，去掉connector function只对原始的学生网络训练分类。

Convolutional neural netwrok

设卷积网络的隐含层神经元个数为 \(H\times W\times M\)（height, width, channel）。由于卷积网络共享每个空间位置的权重，\(H\times W\times M\) 个个神经元响应可以理解为图片上 \(H\times W\) 大小感受野上的一个 \(M\) 维的神经元响应。因此该方法可以应用于神经元响应的每个空间位置。对于一个神经元响应张量 \(\mathcal{T}(I)\in \mathbb{R}^{H\times W\times M}\) 和 \(\mathcal{S}(I)\in \mathbb{R}^{H\times W\times N}\)，位置 \((i,j)\) 处的神经元响应向量分别表示为 \(\mathcal{T}(I)_{ij}\in \mathbb{R}^{M}\) 和 \(\mathcal{S}(I)_{ij}\in \mathbb{R}^{N}\)，\((i=1,...,H;j=1,...,W)\)。本文提出的损失可表示如下

利用式(7)，本文提出的方法就可以用于卷积网络，此时connector函数是一个在所有spatial location共享的 \(1\times 1\) 卷积而不是全连接层。

代码解析

这里的代码是RepDistiller中的第三方实现，其中self.w是不同层的权重，在原文中没有看到。

from __future__ import print_function

import torch
import torch.nn as nn


class ABLoss(nn.Module):
    """Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons
    code: https://github.com/bhheo/AB_distillation
    """
    def __init__(self, feat_num, margin=1.0):
        super(ABLoss, self).__init__()
        self.w = [2**(i-feat_num+1) for i in range(feat_num)]
        self.margin = margin

    def forward(self, g_s, g_t):
        bsz = g_s[0].shape[0]
        losses = [self.criterion_alternative_l2(s, t) for s, t in zip(g_s, g_t)]
        losses = [w * l for w, l in zip(self.w, losses)]
        # loss = sum(losses) / bsz
        # loss = loss / 1000 * 3
        losses = [l / bsz for l in losses]
        losses = [l / 1000 * 3 for l in losses]
        return losses

    def criterion_alternative_l2(self, source, target):
        loss = ((source + self.margin) ** 2 * ((source > -self.margin) & (target <= 0)).float() +
                (source - self.margin) ** 2 * ((source <= self.margin) & (target > 0)).float())
        return torch.abs(loss).sum()