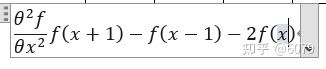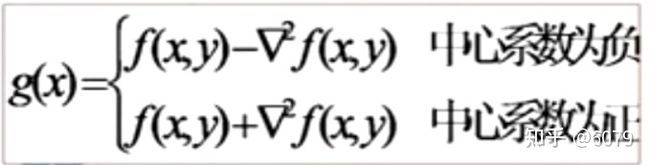拉普拉斯边缘检测_图像处理学习笔记（十四）——图像边缘锐化的基本方法(理论篇)...

本篇文章主要介绍图像边缘锐化的基本方法；

锐化处理的目的是增强边界；图像中的物体的区别是图像的亮度值不同；在边界上反应很大的变化；所以锐化的目的是突出物体的细节，或者增强被模糊了的图像细节；

为了以后边界提取、图像分割、目标识别、形状特征的提取打下基础；

锐化的基本方法：

图像锐化主要靠边界的不同，所以锐化求不同就要求差异，求差异要用减的方法；所以我们用到微分运算；

在微分运算的基础上，介绍梯度锐化和边缘检测；

梯度锐化：保持物体的边界很清晰，使物体的内部数据保留不变，在边缘上增强；除此之外，介绍通用的边缘检测算子，并对这些算子进行比较；

所以本篇文章主要围绕：如何增强边界？？？怎样提取边界？？？

1、增强边界：加强图片中物体的边界，突出边界；不改变物体内部数据量；

2、提取边界：不考虑物体内部信息；

图像边缘类型：

通常，边缘上的灰度变化平缓，而边缘两侧灰度变化比较快，图像的边缘一般是指在局部不连续的图像特征。一般是局部亮度变化最显著的部分，灰度值的变化、颜色分量的突变、纹理结构的突变都可以构成边缘信息；

边缘是有方向性的，一个物体的边缘可能是水平的，也可能是垂直的；只有垂直与边缘的数据量是变化很大的；跟边缘一致的点，变化是很小的；我们不能任意找变化量，必须沿着垂直于边缘的的方向上，才能找到最大的变化量；所以边缘上的变化量是很小的，垂直于边缘的两侧数据量变化很大；

所以要找边缘，就要找数据的变换量，一个方向上的变化量；变化量只能用减法；相邻两个像素的差值；

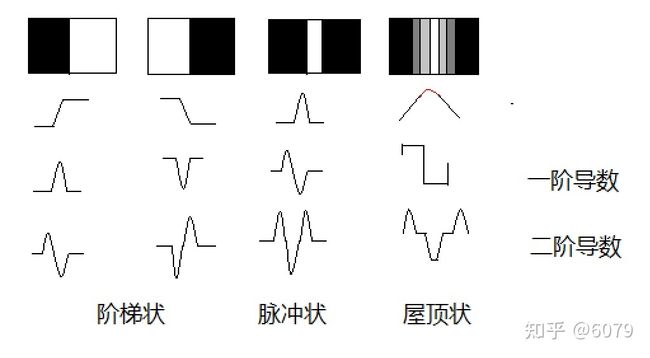
常见的边缘类型：

差分特点：

阶梯状：差分在边缘处有最大值；所以一阶导数有最大值；在进行求导，二阶导数是过零的；

脉冲状：一阶导数有最大值、最小值，也有过零；

屋顶状：有一部分是为0，从零到最高，然后到最低；

我们最感兴趣的是恒定灰度区域(平坦段)、突变的开头与结尾(阶梯与斜坡突变)以及沿着灰度级斜坡处的特性。微分运算能够增强边缘和其他突变(如噪声)，削弱灰度缓慢变化的区域，微分运算的响应强度与图像在该点的突变程度有关；

因为数字图像是离散的，这里用差分定义微分：

一元函数f(x)一阶微分：

一元函数f(x)二阶微分：

对上面的表达式要构成模板，然后对图像的整个数据进行处理计算；

单向微分运算：

方向竖直微分，G表示微分数据：

G(i , j) = f(i , j) - f(i-1 , j)

如上图，从左到右，以第三列为中心，左边为黑，右边为白；

方向水平微分，G表示微分数据：

G(i , j) = - f(i , j - 1) + f(i , j)

如上图，从上到下，以第三行为中心，上边为黑，下边为白；

双向一次微分运算：

我们要获得即获得水平又获得垂直方向的边界，就要进行双向微分；对图像f在纵方向和横方向两个方向进行微分。该算法是同时增强水平和垂直方向的边缘；

微分之后，把纵方向上的微分取平方加上水平方向上的微分取平方，就是双向一次微分；

因为对于边缘上一点来说，在水平方向上和竖直方向上的微分都为0，所以0的平方相加在开平方还是0；因此这个边缘一点还是0；

微分运算的作用：

1、相减的结果反映图像亮度的变化率；

2、像素值保持不变的区域，相减的结果为0，即像素为黑；

3、像素值变化剧烈的区域，相减后得到较大的变化率，像素灰度值变化差别越大，则得到的像素就越亮，图像的垂直边缘得到增强；

梯度运算：

再求边缘方向时，不知道边缘的方向是什么；梯度是一个矢量，分别沿着X和Y计算；在X方向求一次微分，在Y方向求一次微分，这样就构成了矢量，变化率就叫做梯度；

梯度是矢量，我们需要变成标量，一个可测的量；将X和Y分别取绝对值，直接得到梯度，或者把这两个值取最大值，或者对这两个值，平方在开方；就得到梯度；

交叉微分运算

Robert提出交叉微分运算：不是在水平和竖直方向上求梯度，而是在对角线上求梯度；

比如对于图中Z5求梯度；

Gx和Gy这两个梯度取绝对值，或者平方以后在开方；或者取最大值；

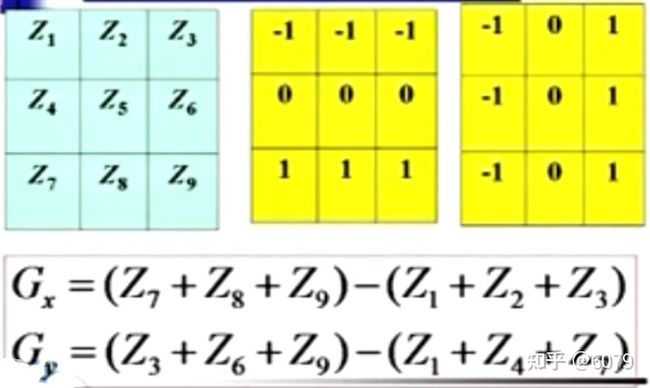
sobel算法：

计算Z5的梯度，先给一个模板：下一行数据平均化减去上一行数据平均化的值；下一列数据平均化减去上一列数据平均化的值；

说明是先平滑然后微分；

Prewitt算法：

Prewitt算法和Sobel算法的区别是：在模板系数上面；

梯度运算时，用模板卷积运算速度会很快，很方便；

在前面介绍平滑的几篇文章中，模板系数都是正值；而目前的模板有正有负，用来求偏差；

二阶微分：

拉普拉斯算法：

求梯度，有两个方向，对每个方向进行二次微分，求和；我们弄明白位置，知道系数是多少，就可以推导出模板：

在数学中有二阶微分公式

在图像中，我们用卷积的方法实现图像的二维数据的微分；

拉普拉斯特点是中间值比较大，靠近中间值得系数也大；

拉普拉斯运算特点：

1、强调突变，同时弱化慢变。产生一副把浅灰色边线、突变点叠加到暗背景中的一副图像；

2、将原始图像和拉普拉斯图像叠加到一起，保持锐化处理的效果，又能复原背景信息；仅仅求完拉普拉斯变换以后，图像非常暗，因为差分以后，尽可能相同的值，都为黑值了，并且两个值一减整个亮度都降了下来；

如果即想加强边界信息，又想保留物体内部信息，往往用下面这个公式，在原始图像的基础上加上梯度值；对中心系数为负值，就用上面这个公式，正的就用下面这个公式；

带入数值之后，得到下图中底下的公式：

根据公式可以推导出如下模板：

用公式计算，很麻烦；如果用模板的方式来处理图像，很方便，计算很快；

高斯——拉普拉斯算法

高斯——拉普拉斯算法是效果更好的边缘检测器，把高斯平滑器和拉普拉斯锐化结合起来，先平滑去噪，在进行边缘检测；

高斯——拉普拉斯模板中心系数很大，距离近的大，距离远的小；

高斯——拉普拉斯算法曲线：

高频提升滤波器

高频就是边界；微分可以求信号的变化率；微分处理后的图像非常暗，不适用；

如果即要保证图像的轮廓清晰，又要保证目标物体的内部灰度不变，就要用到高频提升滤波器；

公式，像素乘以一个系数，然后加上梯度值：

自适应边界检测

采用多个边缘检测算法，不同的检测算法模板采用不同的方向、不同的邻域推导，用卷积方法，计算每个模板，取最大值；

物体的方向有很多，有0°、90°等，我们不知道在哪个方向上取得边界，就可以多个边缘检测算子；比如先看在水平方向有没有边界，然后在看垂直方向，在看45°等等；所以我们需要提供很多方向求方向边界的梯度锐化的模板；哪个模板取得最大值，就认为在哪个方向上是有边界；

实现步骤：

1、将所有边缘模板作用于图像中的每一个像素；

2、产生最大输出值的边缘模板方向；

3、如果所有方向上的边缘模板接近0，该点没有边缘；

4、如果所有方向的边缘模板输出值都近似相等，就没有可靠的边缘方向；

Kirsch边缘检测算法：

先制定了多个方向上的边缘检测模板；然后求得最大值，取最大值；

锐化算法总结：

好的检测结果：对边缘的错误检测率低，在检测出真实边缘的同时，避免检测虚假边缘；

好的边缘定位精度：标记的边缘位置要和图像上真正的边缘位置尽量接近；

对同一边缘要有低的响应次数：有的算法会对一个边缘产生多个响应，本来只有一个边缘点，可能检测出来多个边缘点，克服噪声的影响；

算法比较：

Roberts：对角线相减，定位比较高，但是没有平滑处理，直接减，容易丢失一部分边缘，不具备抗噪声的能力；对陡峭边缘且含噪声少的图像效果较好；

Sobel和Prewitt：在系数上会有差异，有一部分做平滑，在做微分运算；平滑的权值有差异，对噪声有抑制能力，但是不能排除虚假边缘；定位效果不好，容易检测出多像素的宽度；

Laplacian：不依赖于方向，把两个方向都算了。对阶跃型边缘定位很准，对噪声敏感，使噪声加强，噪声能力差；容易造成一部分边缘检测的方向信息，造成一些不连续检测边缘；

高斯Laplacian：先用高斯函数平滑滤波，然后用Laplacian检测边缘，用来克服Laplacian抗噪声的缺点；但同时也平滑掉比较尖锐的边缘，尖锐边缘无法被检测；是属于低通滤波，通频带越窄，对高斯噪声抑制作用越大，避免了虚假边缘的检出，同时信号边缘也被平滑掉，造成某些边缘的丢失；反之，通带越宽，可以检测到更高频率的细节，对噪声抑制能力下降，容易出现虚假边缘。

所以高斯函数中方差参数的选择很关键，对图像边缘检测效果有很大影响；

有理解错误的请大家指出，一起学习一起进步；