x01.Weiqi.1 提子算法

吃饭是为了活着，而活着不是为了吃饭。人生的意义，在于与神对话。有人跳舞，有人卖油，有人杀牛。而我，选择了编程。编程，当然要研究人工智能。人工智能的切入点，是棋类游戏。据说，五子棋算得尽，围棋算不尽。那么，就从算不尽开始吧。

使用 Griphics画线和圆，悔棋时闪烁不已。Dispose！

使用 19 * 19 的 UniformGrid填以 361 个 Tile，两步就不堪重负。Dispose！

最终，采用了用户控件。先建立一个 WPF 应用项目，添加两个 UserControl，分别取名为 Chess 和 Board，将 Chess.xaml 中的 Grid 改为 <Ellipse  Name=”m_Ellipse” />，Board.xaml 中的Grid 改为 <Canvas  Name=”m_Canvas” />。

进入 Chess.xaml.cs 代码文件，修改如下：

Chess

namespace x01.Weiqi
{
public partial class Chess : UserControl
{
public Chess(Brush fillBrush, int size = 38 )
{
InitializeComponent();
m_Ellipse.Fill = fillBrush;
m_Ellipse.Width = m_Ellipse.Height = size;
}
}
}

进入 Board.xaml.cs 代码文件， 修改如下：

namespace x01.Weiqi

{

    public partial class Board : UserControl

    {

Ready

// 为灵活调整而设
public int ChessSize{ get ; set ;}

bool m_IsBlack = false ;
Pos m_NotInPos = new Pos( - 1 , - 1 );
Step[,] m_Steps = new Step[ 19 , 19 ];
int m_Count = 0 ;
List < Pos > m_DeadPos = new List < Pos > ();
List < DeadStep > m_DeadSteps = new List < DeadStep > ();

struct DeadStep
{
public int Count;
public ChessColor Color;

// key 为死子 Count，value 为死子 Column，Row
public Dictionary < int , Pos > DeadInfo;
}

// 本欲用 Point，但 double 类型不方便
struct Pos
{
public int X;
public int Y;

public Pos( int x, int y)
{
X = x;
Y = y;
}
}

enum ChessColor
{
Black, White, Empty
}

// 每一步的棋子信息
struct Step
{
public Chess Chess;
public ChessColor Color;
public bool IsDead;
public int Count;
public int Column;
public int Row;
}

public Board( int size = 38 )
{
InitializeComponent();

ChessSize = size;
Init();
}

void Init()
{
Width = Height = ChessSize * 19 ;
Background = new SolidColorBrush(Color.FromArgb( 0x5e , 0xef , 0xdf , 0x56 ));

for ( int i = 0 ; i < 19 ; i ++ )
{
for ( int j = 0 ; j < 19 ; j ++ )
{
m_Steps[i, j].Chess = null ;
m_Steps[i, j].Color = ChessColor.Empty;
m_Steps[i, j].IsDead = false ;
m_Steps[i, j].Count = - 1 ;
m_Steps[i, j].Row = - 1 ;
m_Steps[i, j].Column = - 1 ;
}
}

// 画线
for ( int i = 0 ; i < 19 ; i ++ )
{
Line l = new Line();
l.Stroke = Brushes.Black;
int y = i * ChessSize + ChessSize / 2 ;
l.X1 = ChessSize / 2 ;
l.Y1 = y;
l.X2 = 19 * ChessSize - ChessSize / 2 ;
l.Y2 = y;
m_Canvas.Children.Add(l);

l = new Line();
l.Stroke = Brushes.Black;
int x = i * ChessSize + ChessSize / 2 ;
l.X1 = x;
l.Y1 = ChessSize / 2 ;
l.X2 = x;
l.Y2 = 19 * ChessSize - ChessSize / 2 ;
m_Canvas.Children.Add(l);
}

// 画星
for ( int j = 0 ; j < 3 ; j ++ )
for ( int i = 0 ; i < 3 ; i ++ )
{
Ellipse e = new Ellipse();
e.Fill = Brushes.Black;
e.Width = 8 ;
e.Height = 8 ;
double left = 4 * ChessSize - ChessSize / 2 + j * 6 * ChessSize;
double top = 4 * ChessSize - ChessSize / 2 + i * 6 * ChessSize;
Canvas.SetLeft(e, left - 4 );
Canvas.SetTop(e, top - 4 );
m_Canvas.Children.Add(e);
}
}

 

BackOne

protected override void OnMouseRightButtonDown(MouseButtonEventArgs e)
{
base .OnMouseRightButtonDown(e);

BackOne();
}

private void BackOne()
{
if (m_Count == 0 )
{
return ;
}

int count = m_Count -- ;
int index = - 1 ;

foreach (var dead in m_DeadSteps)
{
if (dead.Count == count)
{
index = m_DeadSteps.Count - 1 ;
Brush brush;
if (dead.Color == ChessColor.Black)
{
brush = Brushes.Black;
}
else
{
brush = Brushes.White;
}

foreach (var info in dead.DeadInfo)
{
int col = info.Value.X;
int row = info.Value.Y;

Ellipse e = new Ellipse();
e.Fill = brush;
e.Width = e.Height = ChessSize;
m_Steps[col, row].Chess.Content = e;
m_Steps[col, row].Color = dead.Color;
m_Steps[col, row].Count = info.Key;
m_Steps[col, row].Column = col;
m_Steps[col, row].Row = row;
}
}
}

if (index != - 1 )
{
m_DeadSteps.RemoveAt(index);
}

foreach (var item in m_Steps)
{
if (item.Chess != null && item.Count == count)
{
int col = item.Column;
int row = item.Row;
m_Steps[col, row].Chess.Content = null ;
m_Steps[col, row].Count = - 1 ;
m_Steps[col, row].Color = ChessColor.Empty;
m_Steps[col, row].Row = - 1 ;
m_Steps[col, row].Column = - 1 ;
m_IsBlack = ! m_IsBlack;
}
}
}

 

Eat

protected override void OnMouseLeftButtonDown(MouseButtonEventArgs e)
{
base .OnMouseLeftButtonDown(e);

int col = ( int )e.GetPosition( this ).X / ChessSize;
int row = ( int )e.GetPosition( this ).Y / ChessSize;

if (m_Steps[col, row].Color != ChessColor.Empty)
{
return ;
}

if (m_NotInPos.X == col && m_NotInPos.Y == row)
{
return ;
}
else
{
m_NotInPos.X = - 1 ;
m_NotInPos.Y = - 1 ;
}

DrawChess(col, row);

if ( ! EatOther(col, row))
{
if (EatSelf(col, row))
{
// 自杀一子为禁入
if (m_DeadPos.Count == 1 )
{
BackOne();
}
}
}
}

private void DrawChess( int col, int row)
{
int left = col * ChessSize;
int top = row * ChessSize;

Brush brush;
if (m_IsBlack = ! m_IsBlack)
{
brush = Brushes.Black;
m_Steps[col, row].Color = ChessColor.Black;
}
else
{
brush = Brushes.White;
m_Steps[col, row].Color = ChessColor.White;
}

if (m_Steps[col, row].Chess == null )
{
Chess chess = new Chess(brush, ChessSize);
Canvas.SetLeft(chess, left);
Canvas.SetTop(chess, top);
m_Canvas.Children.Add(chess);
m_Steps[col, row].Chess = chess;
}
else if (m_Steps[col, row].Chess.Content == null )
{
Ellipse e = new Ellipse();
e.Fill = brush;
e.Width = e.Height = ChessSize;
m_Steps[col, row].Chess.Content = e;
}
else
{
throw new Exception( string .Format( " Cannot Draw Chess at: col = {0}, row = {1}. " , col, row));
}

m_Steps[col, row].Count = ++ m_Count;
m_Steps[col, row].Column = col;
m_Steps[col, row].Row = row;
}

private bool EatOther( int col, int row)
{
// 上、下、左、右各吃一通。
bool ok1 = false ;
if (col != 0 && m_Steps[col, row].Color != m_Steps[col - 1 , row].Color)
{
ok1 = EatSelf(col - 1 , row);
}
bool ok2 = false ;
if (col != 18 && m_Steps[col, row].Color != m_Steps[col + 1 , row].Color)
{
ok2 = EatSelf(col + 1 , row);
}
bool ok3 = false ;
if (row != 0 && m_Steps[col, row].Color != m_Steps[col, row - 1 ].Color)
{
ok3 = EatSelf(col, row - 1 );
}
bool ok4 = false ;
if (row != 18 && m_Steps[col, row].Color != m_Steps[col, row + 1 ].Color)
{
ok4 = EatSelf(col, row + 1 );
}

return ok1 || ok2 || ok3 || ok4;
}

private bool EatSelf( int col, int row)
{
ClearForEat();
if (CanEat(col, row, m_Steps[col, row].Color))
{
DeadStep deadStep;
deadStep.Count = m_Count;
deadStep.Color = m_Steps[col, row].Color;
deadStep.DeadInfo = new Dictionary < int , Pos > ();
if (m_DeadPos.Count == 1 )
{
Pos pos;
pos.X = m_DeadPos[ 0 ].X;
pos.Y = m_DeadPos[ 0 ].Y;

m_NotInPos.X = pos.X;
m_NotInPos.Y = pos.Y;

foreach (var item in m_Steps)
{
// 变色而已，m_Count 为上一步
if (item.Count == m_Count)
{
ClearForEat();
if (CanEat(pos.X, pos.Y, item.Color))
{
// 因有一子变色，故减一。实际 Count 至少为 3
if (m_DeadPos.Count - 1 > 0 )
{
m_NotInPos.X = - 1 ;
m_NotInPos.Y = - 1 ;
}
}
}
}

deadStep.DeadInfo.Add(m_Steps[pos.X, pos.Y].Count, new Pos(pos.X, pos.Y));

m_Steps[pos.X, pos.Y].Color = ChessColor.Empty;
m_Steps[pos.X, pos.Y].Chess.Content = null ;
}
else
{
foreach (var item in m_DeadPos)
{
deadStep.DeadInfo.Add(m_Steps[item.X, item.Y].Count, new Pos(item.X, item.Y));

m_Steps[item.X, item.Y].Color = ChessColor.Empty;
m_Steps[item.X, item.Y].Chess.Content = null ;
}
}
m_DeadSteps.Add(deadStep);

return true ;
}

return false ;
}

void ClearForEat()
{
foreach (var item in m_DeadPos)
{
m_Steps[item.X, item.Y].IsDead = false ;
}
m_DeadPos.Clear();
}

bool CanEat( int col, int row, ChessColor currentColor)
{
if (m_Steps[col, row].Color == ChessColor.Empty)
{
return false ;
}

m_DeadPos.Add( new Pos(col, row));
m_Steps[col, row].IsDead = true ;

// 边界问题，头疼问题。笨人笨法，分别处理之
return CanEatLeft(col, row, currentColor) && CanEatRight(col, row, currentColor)
&& CanEatUp(col, row, currentColor) && CanEatDown(col, row, currentColor);
}

bool CanEatLeft( int col, int row, ChessColor currentColor)
{
if (col != 0 )
{
if (m_Steps[col - 1 , row].Color == ChessColor.Empty)
{
return false ;
}
else if (m_Steps[col - 1 , row].Color == currentColor && m_Steps[col - 1 , row].IsDead == false )
{
m_DeadPos.Add( new Pos(col - 1 , row));
m_Steps[col - 1 , row].IsDead = true ;
if ( ! CanEatUp(col - 1 , row, currentColor))
{
return false ;
}
if ( ! CanEatDown(col - 1 , row, currentColor))
{
return false ;
}
if ( ! CanEatLeft(col - 1 , row, currentColor))
{
return false ;
}
}
}

return true ;
}

bool CanEatRight( int col, int row, ChessColor currentColor)
{
if (col != 18 )
{
if (m_Steps[col + 1 , row].Color == ChessColor.Empty)
{
return false ;
}
else if (m_Steps[col + 1 , row].Color == currentColor && m_Steps[col + 1 , row].IsDead == false )
{
m_DeadPos.Add( new Pos(col + 1 , row));
m_Steps[col + 1 , row].IsDead = true ;
if ( ! CanEatUp(col + 1 , row, currentColor))
{
return false ;
}
if ( ! CanEatDown(col + 1 , row, currentColor))
{
return false ;
}
if ( ! CanEatRight(col + 1 , row, currentColor))
{
return false ;
}
}
}

return true ;
}

bool CanEatUp( int col, int row, ChessColor currentColor)
{
if (row != 0 )
{
if (m_Steps[col, row - 1 ].Color == ChessColor.Empty)
{
return false ;
}
else if (m_Steps[col, row - 1 ].Color == currentColor && m_Steps[col, row - 1 ].IsDead == false )
{
m_DeadPos.Add( new Pos(col, row - 1 ));
m_Steps[col, row - 1 ].IsDead = true ;
if ( ! CanEatLeft(col, row - 1 , currentColor))
{
return false ;
}
if ( ! CanEatRight(col, row - 1 , currentColor))
{
return false ;
}
if ( ! CanEatUp(col, row - 1 , currentColor))
{
return false ;
}
}
}

return true ;
}

bool CanEatDown( int col, int row, ChessColor currentColor)
{
if (row != 18 )
{
if (m_Steps[col, row + 1 ].Color == ChessColor.Empty)
{
return false ;
}
else if (m_Steps[col, row + 1 ].Color == currentColor && m_Steps[col, row + 1 ].IsDead == false )
{
m_DeadPos.Add( new Pos(col, row + 1 ));
m_Steps[col, row + 1 ].IsDead = true ;
if ( ! CanEatLeft(col, row + 1 , currentColor))
{
return false ;
}
if ( ! CanEatRight(col, row + 1 , currentColor))
{
return false ;
}
if ( ! CanEatDown(col, row + 1 , currentColor))
{
return false ;
}
}
}

return true ;
}

    }

}

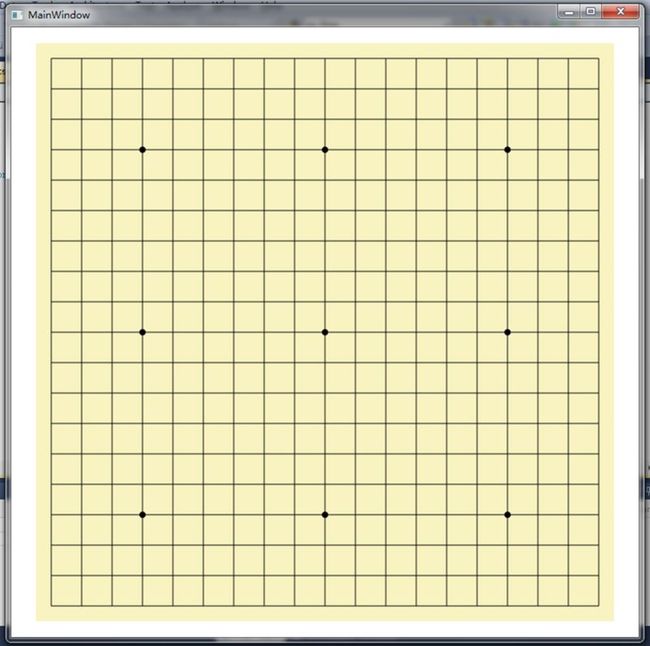
编译生成后，将工具栏上的 Board 控件拖入主窗口即可。

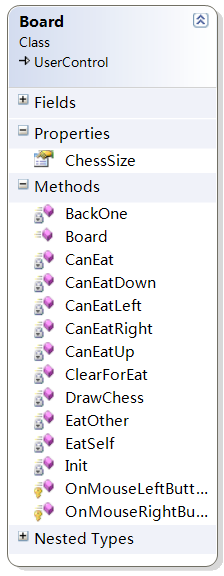
Board 图示如下:

                    

首先吃对方 EatOther，吃对方又可转化为吃自己 EatSelf， 吃自己的关键在于 CanEat， CanEat 的实现，采用分而治之的方针： CanEatUp， CanEatDown， CanEatLeft， CanEatRight。上下左右，各吃一通！

 

               两句三年得，

               一吟泪双流。

               知音如不赏，

               归卧故山秋。

 

代码可从 http://www.cnblogs.com/china_x01 的 Download/Code/x01.Weiqi 获取。

效果图如下：

              

Copyright (c) 2011 by x01 ([email protected])，未经本人许可，请勿擅自转载。