《算法系列》之滑动窗口
简介
其实滑动窗口是一类特殊的双指针类型题,两个指针同向移动,我们更关心两个指针内所包含的数据,这时就可以称为滑动窗口类型的题了,很多解法我们很自然的就能想到用滑动窗口去解决,比如,“在一个数组中,那段连续元素相加等于target”。这种一看就知道,应该用两个指针做滑动窗口,然后计算包含的值的结果即可,总不可能用循环嘛对不对。
理论基础
滑动窗口其实理论基础就是双指针,指的是一类问题的求解方法,在数组上通过双指针同向移动而解决的一类问题。其实我们可以不必为它们专门命名一个名字,它们的解法其实是很自然的。不过使用滑动窗口解决的问题通常是暴力解法的优化,掌握这一类问题最好的办法就是练习,然后思考清楚为什么可以使用滑动窗口。
解题心得
- 滑动窗口也可以看做是特殊的双指针题目,双指针同向移动而解决的一类问题。
- 滑动窗口和双指针最大的区别是,滑动窗口更关心窗口内的值,而不只两个指针上的元素。
- 使用滑动窗口解决的问题通常是暴力解法的优化。
- 经典滑动窗口需要了解与掌握。
- 很多时间滑动窗口会和哈希表一起使用。
- 需要多加练习,然后思考清楚为什么使用滑动窗口。
算法题目
3. 无重复字符的最长子串
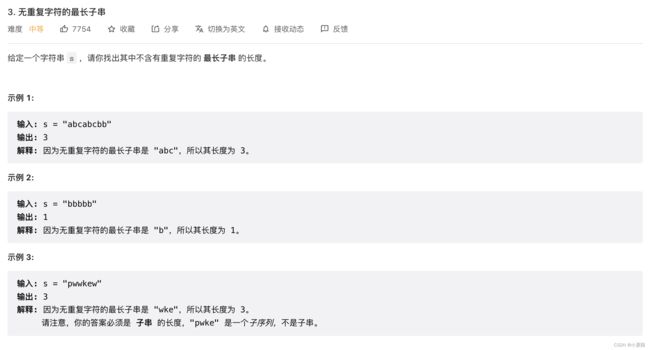
题目解析:用滑动窗口思想解题即可,用两个指针选择子串,然后用哈希表判断是否有重复。
代码如下:
/**
*
*/
class Solution {
public int lengthOfLongestSubstring(String s) {
int ans = 0;
char[] arr = s.toCharArray();
Map map = new HashMap<>();
for (int j = 0, i = 0; j < arr.length; j++) {
if (map.containsKey(arr[j])) {
i = Math.max(map.get(arr[j]), i);
}
ans = Math.max(ans, j - i + 1);
map.put(arr[j], j + 1);//下标 + 1 代表 i 要移动的下个位置
}
return ans;
}
}
30. 串联所有单词的子串

题目解析:记words的长度为m,words中每个单词的长度为n,s的长度为ls。 首先需要将s划分为单词组,每个单词的大小均为n (首尾除外)。这样的划分方法有n种,即先删去前i (i=0≈n-1) 个字母后,将剩下的字母进行划分,如果末尾有不到n个字母也删去。对这n种划分得到的单词数组分别使用滑动窗口对words进行类似于字母异位词的搜寻。
代码如下:
/**
* 滑动窗口
*/
class Solution {
public List findSubstring(String s, String[] words) {
List res = new ArrayList();
int m = words.length, n = words[0].length(), ls = s.length();
for (int i = 0; i < n; i++) {
if (i + m * n > ls) {
break;
}
Map differ = new HashMap();
for (int j = 0; j < m; j++) {
String word = s.substring(i + j * n, i + (j + 1) * n);
differ.put(word, differ.getOrDefault(word, 0) + 1);
}
for (String word : words) {
differ.put(word, differ.getOrDefault(word, 0) - 1);
if (differ.get(word) == 0) {
differ.remove(word);
}
}
for (int start = i; start < ls - m * n + 1; start += n) {
if (start != i) {
String word = s.substring(start + (m - 1) * n, start + m * n);
differ.put(word, differ.getOrDefault(word, 0) + 1);
if (differ.get(word) == 0) {
differ.remove(word);
}
word = s.substring(start - n, start);
differ.put(word, differ.getOrDefault(word, 0) - 1);
if (differ.get(word) == 0) {
differ.remove(word);
}
word = s.substring(start - n, start);
}
if (differ.isEmpty()) {
res.add(start);
}
}
}
return res;
}
}
76. 最小覆盖子串

题目解析:使用右指针不断扩张,去寻找一个可行解,找到可行解之后,使用左指针进行收缩,优化可行解,同时更新结果,一次遍历即可得到最终解。
代码如下:
/**
* 滑动窗口
*/
class Solution {
public String minWindow(String s, String t) {
HashMap need = new HashMap<>(); // 用来保存所需要匹配的字符个数
HashMap window = new HashMap<>(); // 用来保存当前窗口内能满足匹配的字符个数
int left = 0, right = 0; // 左右窗口指针,逻辑上定义为左闭右开的区间,这样的话[0,0)时,区间内就没有元素,方便边界处理
int valid = 0; // 记录当前window有多少个字符满足need,当全部满足时,开始收缩左指针
int start = 0, end = 0; // 记录满足条件字符串的起始位置
int len = Integer.MAX_VALUE; // 记录满足条件的字符串的长度,用于更新最终结果
// 初始化need
for(int i = 0; i < t.length(); i++){
need.put(t.charAt(i), need.getOrDefault(t.charAt(i), 0) + 1); // 将相应的键值对存入need
}
// 滑动窗口开始工作
while(right < s.length()){ // 保证right遍历了整个字符串
// 先右窗口扩张,找到可行解
char in_ch = s.charAt(right);
right++;
if(need.containsKey(in_ch)){ // 如果遍历到的是我们需要的字符,则将其加入window中,保证need和window保存的是同种字符
window.put(in_ch, window.getOrDefault(in_ch, 0) + 1);
if(window.get(in_ch).equals(need.get(in_ch))){ // 第一次相等时更新valid, 注意Integer对象要用equals来进行比较,不能用 ==
valid++; // 表示有一个字符已经满足了
}
}
// 如果valid全部满足,则去收缩左窗口,优化可行解
while(valid == need.size()){
// 保存当前解
if(len > right - left){
len = right-left;
start = left;
end = right;
}
// 同时收缩左窗口,优化当前可行解
char out_ch = s.charAt(left);
left++;
if(need.containsKey(out_ch)){
if(window.get(out_ch).equals(need.get(out_ch))){ // 因为window内的某字符数量可能多于need中的,所以当相等的时候再--
valid--;
}
window.put(out_ch, window.get(out_ch)-1); // 同时window内该字符数量-1
}
}
}
return s.substring(start, end);
}
}
187. 重复的DNA序列
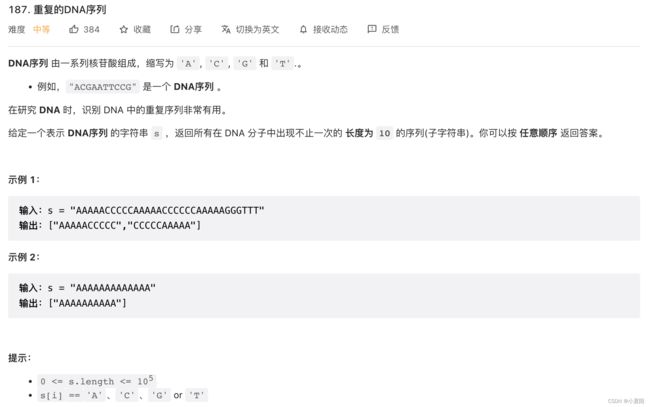
题目解析:用一个哈希表统计 s 所有长度为 10 的子串的出现次数,返回所有出现次数超过 10 的子串。
代码如下:
/**
* 滑动窗口 + 哈希表
*/
class Solution {
public List findRepeatedDnaSequences(String s) {
Set set = new HashSet();
List res = new ArrayList();
int len = s.length();
if(len <= 10) return res;
for(int i = 0; i < len - 9; i++){
String str =s.substring(i, i + 10);
if(!set.add(str) && !res.contains(str))res.add(str);
}
return res;
}
}
209. 长度最小的子数组
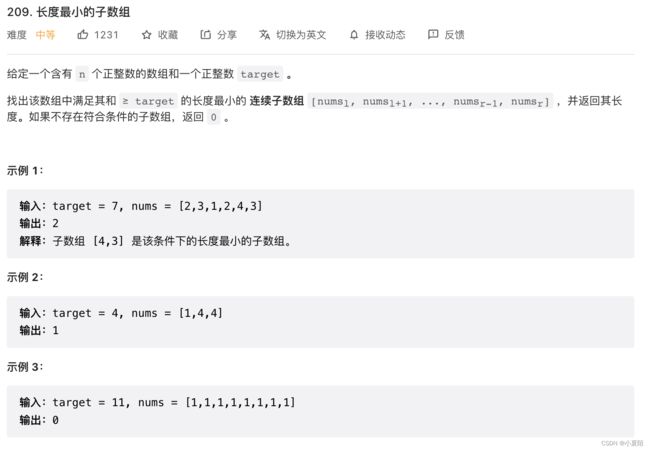
题目解析:滑动窗口经典题,用一个int值比较各窗口值大小即可。
代码如下:
/**
* 滑动窗口
*/
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int left = 0;
int sum = 0;
int result = Integer.MAX_VALUE;
for (int right = 0; right < nums.length; right++) {
sum += nums[right];
while (sum >= s) {
result = Math.min(result, right - left + 1);
sum -= nums[left++];
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}
220. 存在重复元素 III

题目解析:对于序列中每一个元素x左侧的至多k个元素,如果这k个元素中存在一个元素落在区间[x- t, x +t]中,我们就找到了一对符合条件的元素。注意到对于两个相邻的元素,它们各自的左侧的k个元素中有k-1个是重合的。于是我们可以使用滑动窗口的思路,维护一一个大小为k的滑动窗口,每次遍历到元素x时,滑动窗口中包含元素x前面的最多k个元素,我们检查窗口中是否存在元素落在区间[x - t, x + t]中即可。
代码如下:
/**
* 滑动窗口 + 有序集合
*/
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
// 滑动窗口结合查找表,此时滑动窗口即为查找表本身(控制查找表的大小即可控制窗口大小)
TreeSet set = new TreeSet<>();
for (int i = 0; i < nums.length; i++) {
// 边添加边查找
// 查找表中是否有大于等于 nums[i] - t 且小于等于 nums[i] + t 的值
Long ceiling = set.ceiling((long) nums[i] - (long) t);
if (ceiling != null && ceiling <= ((long) nums[i] + (long) t)) {
return true;
}
// 添加后,控制查找表(窗口)大小,移除窗口最左边元素
set.add((long) nums[i]);
if (set.size() == k + 1) {
set.remove((long) nums[i - k]);
}
}
return false;
}
}
239. 滑动窗口最大值
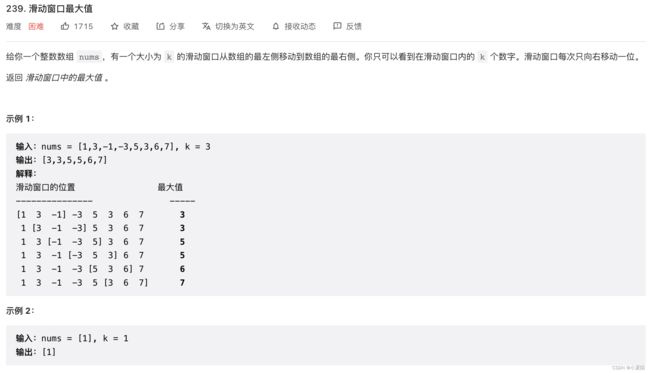
题目解析:利用双端队列手动实现单调队列,用一个单调队列来存储对应的下标,每当窗口滑动的时候,直接取队列的头部指针对应的值放入结果集即可。单调队列类似 (tail -->) 3 --> 2 --> 1 --> 0 (–> head) (右边为头结点,元素存的是下标)。
代码如下:
/**
* 单调队列
*/
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
ArrayDeque deque = new ArrayDeque<>();
int n = nums.length;
int[] res = new int[n - k + 1];
int idx = 0;
for (int i = 0; i < n; i++) {
// 根据题意,i为nums下标,是在[i - k + 1, i] 中选到最大值,只需要保证两点
// 1.队列头结点需要在[i - k + 1, i]范围内,不符合则要弹出
while (!deque.isEmpty() && deque.peek() < i - k + 1) {
deque.poll();
}
// 2.既然是单调,就要保证每次放进去的数字要比末尾的都大,否则也弹出
while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
deque.offer(i);
// 因为单调,当i增长到符合第一个k范围的时候,每滑动一步都将队列头节点放入结果就行了
if (i >= k - 1) {
res[idx++] = nums[deque.peek()];
}
}
return res;
}
}
回到首页
刷 leetcode 500+ 题的一些感受
下一篇
《算法系列》之排序