Adaptive Backstepping Besign自适应反步控制设计
Adaptive Backstepping Besign自适应反步控制设计
目录
- Adaptive Backstepping Besign自适应反步控制设计
-
- 前言
- 1. 基于反步法的跟踪控制设计
-
- 问题描述
- 控制器设计
- 小结
- 2.基于自适应反步控制的跟踪控制设计
-
- 问题描述
- 控制器设计
- 小结
前言
前面的文章分别涉及了自适应控制、自适应神经网络控制、模型参考自适应控制的内容,文章分别对应:
具有不确定参数系统的自适应跟踪控制设计_ADi_hhh的博客
自适应神经网络控制的应用举例_ADi_hhh的博客
(SISO)单输入单输出系统的模型参考自适应控制_ADi_hhh的博客
但其中涉及的最多是MIMO的线性系统,即多变量线性系统。其可以写成这样的形式:
x ˙ = A x + B u y = C x \begin{aligned} \dot x&=Ax+Bu\\ y&=Cx \end{aligned} x˙y=Ax+Bu=Cx
但针对非线性系统
x ˙ 1 = x 1 2 + x 2 x ˙ 2 = 2 x 1 3 + x 1 x 2 + u y = x 1 \begin{aligned} \dot x_1&=x_1^2+x_2\\ \dot x_2&=2x_1^3+x_1x_2+u\\ y&=x_1 \end{aligned} x˙1x˙2y=x12+x2=2x13+x1x2+u=x1
这样的非线性系统如何设置控制器,实现系统的镇定控制和跟踪控制那?如果这样的非线性系统中有未知参数又该怎么办那?
Backstepping方法能通过结构化的设计方法拆解设计过程,从而使得设计变得如同上山的路一样,虽有压力,却也是一步步可以抵达山巅。前面的文章中我们也有使用反步法进行设计控制器的例子:基于反步法的异构模型编队控制器设计_ADi_hhh的博客。关于Backestepping反步设计,可以通过搜索引擎以获得更多的背景信息
本文从反步法入手,进而介绍反步法和自适应控制相结合设计控制器的过程。
1. 基于反步法的跟踪控制设计
问题描述
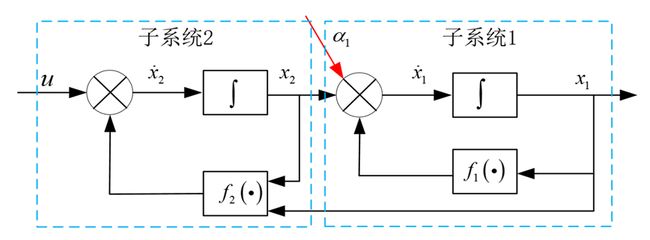
考虑如下系统
x ˙ 1 = f 1 ( x 1 ) + x 2 x ˙ 2 = f 2 ( x 1 , x 2 ) + u y = x 1 \begin{aligned} \dot x_1&=f_1(x_1)+x_2\\ \dot x_2&=f_2(x_1,x_2)+u\\ y&=x_1 \end{aligned} x˙1x˙2y=f1(x1)+x2=f2(x1,x2)+u=x1
其中 f 1 ( x 1 ) 、 f 2 ( x 1 , x 2 ) f_1(x_1)、f_2(x_1,x_2) f1(x1)、f2(x1,x2)是已知的,设计控制器使得 y → y d y→y_d y→yd,并且 y d y_d yd的导数可知。
按照之前设计控制器的流程化结构,设计控制器。
控制器设计
-
定义系统误差: e 1 = y − y d = x 1 − y d e_1=y-y_d=x_1-y_d e1=y−yd=x1−yd
-
系统误差的动态方程:
e ˙ = x ˙ 1 − y ˙ d = f 1 ( x 1 ) + x 2 − y ˙ d \begin{equation} \begin{aligned} \dot e &=\dot x_1 -\dot y_d\\ &=f_1(x_1)+x_2-\dot y_d \end{aligned} \end{equation} e˙=x˙1−y˙d=f1(x1)+x2−y˙d -
考虑如下候选李亚普诺夫函数: V 1 = 1 2 e 2 V_1 = \frac{1}{2}e^2 V1=21e2
对其求导得:
V ˙ 1 = e e ˙ = e ( f 1 ( x 1 ) + x 2 − y ˙ d ) \begin{aligned} \dot V_1 &=e\dot e\\ & = e(f_1(x_1)+x_2-\dot y_d) \end{aligned} V˙1=ee˙=e(f1(x1)+x2−y˙d)
这时候我们可以把 x 2 x_2 x2当作一个输入量,那么假如
x 2 = − k 1 e − f 1 ( x 1 ) + y ˙ d ( 2 ) x_2=-k_1e-f_1(x_1)+\dot y_d \qquad(2) x2=−k1e−f1(x1)+y˙d(2)
那么 V ˙ 1 \dot V_1 V˙1就能够达到负定的形式。可惜我们不能直接令 x 2 x_2 x2成为我们想要的形式,不过我们可以引入一虚拟控制量 α 1 \alpha_1 α1,其实可以看做是 x 2 d x_{2d} x2d,即 x 2 x_2 x2的预期设定值。即令
α 1 = − k 1 e − f 1 ( x 1 ) + y ˙ d ( 3 ) \alpha_1=-k_1e-f_1(x_1)+\dot y_d \qquad(3) α1=−k1e−f1(x1)+y˙d(3)
此时可以定义出第二个误差为 e 2 = x 2 − α 1 e_2=x_2-\alpha_1 e2=x2−α1将 x 2 = e 2 + α 1 x_2=e_2+\alpha_1 x2=e2+α1代入到公式(1)时,
e ˙ = f 1 ( x 1 ) + e 2 + α 1 − y ˙ d \begin{aligned} \dot e &=f_1(x_1)+e_2+\alpha_1-\dot y_d \end{aligned} e˙=f1(x1)+e2+α1−y˙d
则
V ˙ 1 = e e ˙ = e ( f 1 ( x 1 ) + e 2 + α 1 − y ˙ d ) = e ( − k 1 e + e 2 ) = − k 1 e 2 + e e 2 \begin{aligned} \dot V_1 &=e\dot e\\ & = e(f_1(x_1)+e_2+\alpha_1-\dot y_d)\\ &= e(-k_1e+e_2)\\ &=-k_1e^2+ee_2 \end{aligned} V˙1=ee˙=e(f1(x1)+e2+α1−y˙d)=e(−k1e+e2)=−k1e2+ee2
其中 e e 2 ee^2 ee2称为互联项,在之后进行处理。 -
写出误差 e 2 e_2 e2的动态方程
e ˙ 2 = x ˙ 2 − α ˙ 1 = f 2 ( x 1 , x 2 ) + u − α ˙ 1 \begin{aligned} \dot e_2&=\dot x_2-\dot \alpha_1\\ &=f_2(x_1,x_2)+u-\dot \alpha_1 \end{aligned} e˙2=x˙2−α˙1=f2(x1,x2)+u−α˙1
其中 α ˙ 1 \dot \alpha_1 α˙1为已知可求的,其本身是一个复合函数,如果内部含有未知参数,要表示出来,下一篇文章中的例子正是这样。 -
考虑新的候选李雅普诺夫函数 V 2 = V 1 + 1 2 e 2 2 V_2=V_1+\frac{1}{2}e_2^2 V2=V1+21e22
求导得:
V ˙ 2 = V ˙ 1 + e 2 e ˙ 2 = − k 1 e 2 + e e 2 + e 2 ( f 2 ( x 1 , x 2 ) + u − α ˙ 1 ) = − k 1 e 2 + e 2 ( e + f 2 ( x 1 , x 2 ) + u − α ˙ 1 ) \begin{aligned} \dot V_2&=\dot V_1+e_2 \dot e_2\\ &=-k_1e^2+ee_2+e_2(f_2(x_1,x_2)+u-\dot \alpha_1)\\ &=-k_1e^2+e_2(e+f_2(x_1,x_2)+u-\dot \alpha_1)\\ \end{aligned} V˙2=V˙1+e2e˙2=−k1e2+ee2+e2(f2(x1,x2)+u−α˙1)=−k1e2+e2(e+f2(x1,x2)+u−α˙1)
此时可以设计
u = − k 2 e 2 − e − f 2 ( x 1 , x 2 ) + α ˙ 1 ( 4 ) u=-k_2e_2-e-f_2(x_1,x_2)+\dot \alpha_1 \qquad(4) u=−k2e2−e−f2(x1,x2)+α˙1(4)
即可使得 V ˙ 2 \dot V_2 V˙2成为负定的形式。从而公式(4)即为所设计的控制器。
小结
上述过程即为比较啰嗦的反步法控制器设计。
2.基于自适应反步控制的跟踪控制设计
问题描述
考虑如下系统
x ˙ 1 = f 1 ( x 1 ) + x 2 x ˙ 2 = f 2 ( x 1 , x 2 ) θ + b u y = x 1 \begin{aligned} \dot x_1&=f_1(x_1)+x_2\\ \dot x_2&=f_2(x_1,x_2)\theta+bu\\ y&=x_1 \end{aligned} x˙1x˙2y=f1(x1)+x2=f2(x1,x2)θ+bu=x1
其中 f 1 ( x 1 ) 、 f 2 ( x 1 , x 2 ) f_1(x_1)、f_2(x_1,x_2) f1(x1)、f2(x1,x2)是已知的, θ \theta θ时未知的,设计控制器使得 y → y d y→y_d y→yd,并且 y d y_d yd的导数可知。
看到其中含有未知参数,我们应该想到前面的文章中我们利用自适应控制来估计参数。
控制器设计
-
定义系统误差: e 1 = y − y d = x 1 − y d e_1=y-y_d=x_1-y_d e1=y−yd=x1−yd
-
系统误差的动态方程:
e ˙ = x ˙ 1 − y ˙ d = f 1 ( x 1 ) + x 2 − y ˙ d ( 5 ) \begin{aligned} \dot e &=\dot x_1 -\dot y_d\\ &=f_1(x_1)+x_2-\dot y_d \end{aligned} \qquad(5) e˙=x˙1−y˙d=f1(x1)+x2−y˙d(5) -
考虑如下候选李亚普诺夫函数: V 1 = 1 2 e 2 V_1 = \frac{1}{2}e^2 V1=21e2
对其求导得:
V ˙ 1 = e e ˙ = e ( f 1 ( x 1 ) + x 2 − y ˙ d ) \begin{aligned} \dot V_1 &=e\dot e\\ & = e(f_1(x_1)+x_2-\dot y_d) \end{aligned} V˙1=ee˙=e(f1(x1)+x2−y˙d)
这时候我们可以把 x 2 x_2 x2当作一个输入量,那么假如
x 2 = − k 1 e − f 1 ( x 1 ) + y ˙ d ( 6 ) x_2=-k_1e-f_1(x_1)+\dot y_d \qquad(6) x2=−k1e−f1(x1)+y˙d(6)
那么 V ˙ 1 \dot V_1 V˙1就能够达到负定的形式。引入一虚拟控制量 α 1 \alpha_1 α1,即令
α 1 = − k 1 e − f 1 ( x 1 ) + y ˙ d ( 7 ) \alpha_1=-k_1e-f_1(x_1)+\dot y_d \qquad(7) α1=−k1e−f1(x1)+y˙d(7)
此时可以定义出第二个误差为 e 2 = x 2 − α 1 e_2=x_2-\alpha_1 e2=x2−α1将 x 2 = e 2 + α 1 x_2=e_2+\alpha_1 x2=e2+α1代入到公式(5)时,
e ˙ = f 1 ( x 1 ) + e 2 + α 1 − y ˙ d \begin{aligned} \dot e &=f_1(x_1)+e_2+\alpha_1-\dot y_d \end{aligned} e˙=f1(x1)+e2+α1−y˙d
则
V ˙ 1 = e e ˙ = e ( f 1 ( x 1 ) + e 2 + α 1 − y ˙ d ) = e ( − k 1 e + e 2 ) = − k 1 e 2 + e e 2 \begin{aligned} \dot V_1 &=e\dot e\\ & = e(f_1(x_1)+e_2+\alpha_1-\dot y_d)\\ &= e(-k_1e+e_2)\\ &=-k_1e^2+ee_2 \end{aligned} V˙1=ee˙=e(f1(x1)+e2+α1−y˙d)=e(−k1e+e2)=−k1e2+ee2
其中 e e 2 ee^2 ee2称为互联项,在之后进行处理。 -
写出误差 e 2 e_2 e2的动态方程
e ˙ 2 = x ˙ 2 − α ˙ 1 = f 2 ( x 1 , x 2 ) θ + b u − α ˙ 1 \begin{aligned} \dot e_2&=\dot x_2-\dot \alpha_1\\ &=f_2(x_1,x_2)\theta+bu-\dot \alpha_1 \end{aligned} e˙2=x˙2−α˙1=f2(x1,x2)θ+bu−α˙1
其中 α ˙ 1 \dot \alpha_1 α˙1为已知可求的,其本身是一个复合函数。其中含有未知参数 θ \theta θ,我们可以用 θ ^ \hat \theta θ^来估计它,估计误差为 θ ~ = θ ^ − θ \tilde \theta=\hat \theta-\theta θ~=θ^−θ
-
考虑新的候选李雅普诺夫函数 V 2 = V 1 + 1 2 e 2 2 + 1 2 γ θ ~ 2 V_2=V_1+\frac{1}{2}e_2^2+\frac{1}{2 \gamma}\tilde \theta^2 V2=V1+21e22+2γ1θ~2,其中 γ \gamma γ为参数调节率,前几篇文章中都提到过。
求导得:
V ˙ 2 = V ˙ 1 + e 2 e ˙ 2 + 1 γ θ ~ θ ^ ˙ = − k 1 e 2 + e e 2 + e 2 ( f 2 ( x 1 , x 2 ) θ + b u − α ˙ 1 ) + 1 γ θ ~ θ ^ ˙ = − k 1 e 2 + e 2 ( e + f 2 ( x 1 , x 2 ) θ + b u − α ˙ 1 ) + 1 γ θ ~ θ ^ ˙ \begin{aligned} \dot V_2&=\dot V_1+e_2 \dot e_2+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=-k_1e^2+ee_2+e_2(f_2(x_1,x_2)\theta+bu-\dot \alpha_1)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=-k_1e^2+e_2(e+f_2(x_1,x_2)\theta+bu-\dot \alpha_1)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ \end{aligned} V˙2=V˙1+e2e˙2+γ1θ~θ^˙=−k1e2+ee2+e2(f2(x1,x2)θ+bu−α˙1)+γ1θ~θ^˙=−k1e2+e2(e+f2(x1,x2)θ+bu−α˙1)+γ1θ~θ^˙
此时可以设计
b u = − k 2 e 2 − e − f 2 ( x 1 , x 2 ) θ ^ + α ˙ 1 ( 8 ) bu=-k_2e_2-e-f_2(x_1,x_2)\hat \theta+\dot \alpha_1 \qquad(8) bu=−k2e2−e−f2(x1,x2)θ^+α˙1(8)
将公式(8)带入到 V ˙ 2 \dot V_2 V˙2中去,得:
V ˙ 2 = − k 1 e 2 + e 2 ( e + f 2 ( x 1 , x 2 ) θ + b u − α ˙ 1 ) + 1 γ θ ~ θ ^ ˙ = − k 1 e 2 + e 2 ( e + f 2 ( x 1 , x 2 ) θ + ( − k 2 e 2 − e − f 2 ( x 1 , x 2 ) θ ^ + α ˙ 1 ) − α ˙ 1 ) + 1 γ θ ~ θ ^ ˙ = − k 1 e 2 − k 2 e 2 + θ ~ ( − e 2 f 2 ( x 1 , x 2 ) + 1 γ θ ^ ˙ ) \begin{aligned} \dot V_2&=-k_1e^2+e_2(e+f_2(x_1,x_2)\theta+bu-\dot \alpha_1)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=-k_1e^2+e_2(e+f_2(x_1,x_2)\theta+(-k_2e_2-e-f_2(x_1,x_2)\hat \theta+\dot \alpha_1)-\dot \alpha_1)+\frac{1}{\gamma}\tilde \theta \dot{\hat \theta}\\ &=-k_1e^2-k_2e^2+\tilde \theta(-e_2f_2(x_1,x_2)+\frac{1}{\gamma} \dot{\hat \theta}) \end{aligned} V˙2=−k1e2+e2(e+f2(x1,x2)θ+bu−α˙1)+γ1θ~θ^˙=−k1e2+e2(e+f2(x1,x2)θ+(−k2e2−e−f2(x1,x2)θ^+α˙1)−α˙1)+γ1θ~θ^˙=−k1e2−k2e2+θ~(−e2f2(x1,x2)+γ1θ^˙)
设计参数更新率为:
θ ^ ˙ = γ e 2 f 2 ( x 1 , x 2 ) ( 9 ) \dot{\hat \theta}=\gamma e_2f_2(x_1,x_2) \qquad(9) θ^˙=γe2f2(x1,x2)(9)
即可使得 V ˙ 2 \dot V_2 V˙2成为负定的形式。从而公式(8)和公式(9)即为所设计的控制器和参数更新率。
小结
上述设计跟第一部分没有未知参数的设计不一样的地方主要集中在第四步中对于未知参数的处理,而这一部分处理又与前面的文章中的自适应控制设计类似。
上文主要介绍了反步法的控制设计及自适应反步控制的设计。其中未知参数出现在匹配通道上,比较容易设计,下一篇文章主要介绍不匹配条件下的自适应反步控制及自适应神经网络反步控制设计。
如果觉得我写的不错,请给我一个免费的赞,如有错误,也欢迎向我反馈。