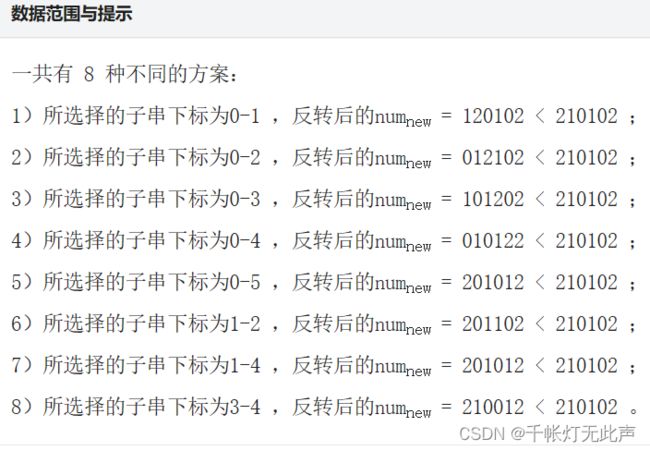
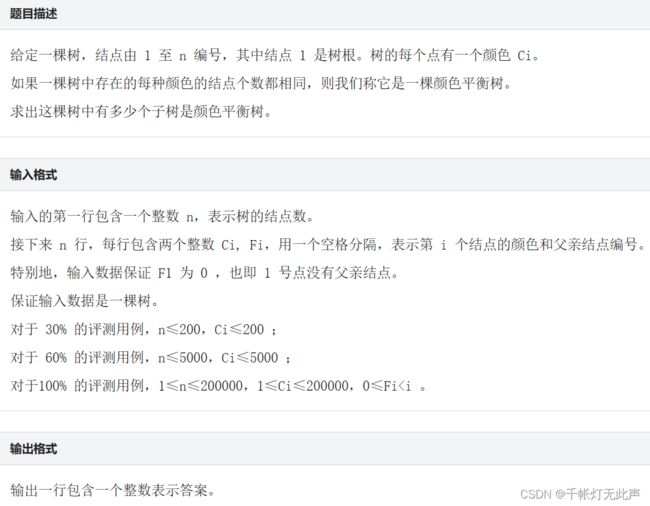
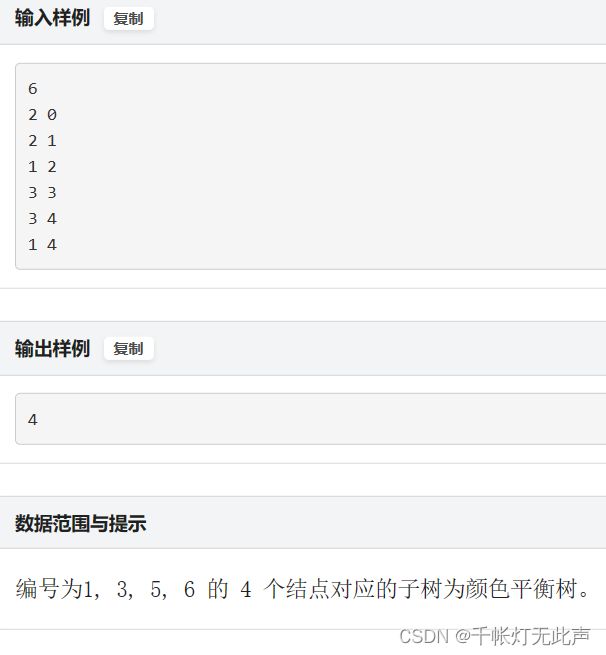
2023蓝桥杯C++A组题解(第十四届)
面向爆零选手
水平有限,将就着看,有空再补充后5题
目录
吐槽
A,2067: [蓝桥杯2023初赛] 幸运数
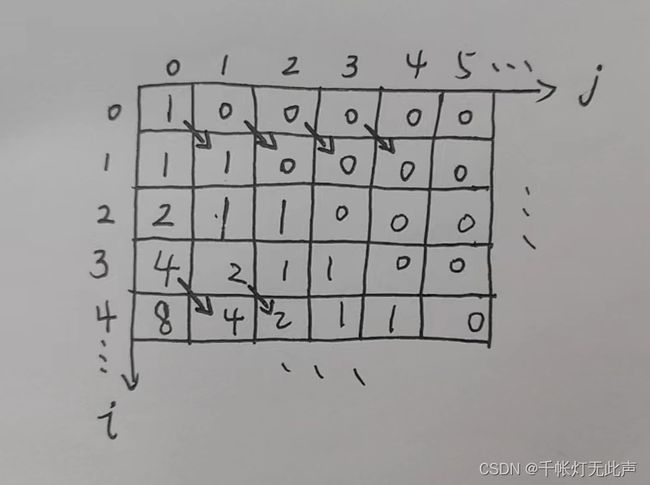
B,2068: [蓝桥杯2023初赛] 有奖问答
AC DFS
AC DP
C,2069: [蓝桥杯2023初赛] 平方差
AC 28% 暴力
AC 92% O(n)
AC 100% O(1)
D,2070: [蓝桥杯2023初赛] 更小的数
AC 44% s.substr
AC DP
AC 常规
E,2071: [蓝桥杯2023初赛] 颜色平衡树
AC 9% 暴力
AC 按秩合并
AC 启发式合并
材料
G:并查集,维护网络连通性
H:异或和之和
吐槽
先吐槽下,比赛结束才发现的技巧 ---- 打表,以前只是知道这个东西,但一直不知道到底是个什么
所谓“暴搜挂着机,打表出省一”,不是没道理的,以前的理解还不到位
暴搜就是暴力2层,3层,4层for循环或者dfs暴力
挂着机就是程序需要十几秒甚至几分钟才能输出完(数据量大,复杂度高)
---->
这么说填空题当然可以直接等输出
编程题也能cout输出中间过程,然后cout前几十个数据(打表),至少拿30%分,运气好直接靠打表AC也不是没可能
(所以今年有人靠着打表,做了四五题,哪怕他不会,在看懂样例的基础上,就能拿多10~20分)
A,2067: [蓝桥杯2023初赛] 幸运数
P2067 - [蓝桥杯2023初赛] 幸运数 - New Online Judge (ecustacm.cn)
标签:入门题,模拟,枚举
思路
写个统计位数的函数,保证数位len % 2 == 0
再写个计算前半数位和,以及后半数位和,判断相等(这里采取整数除以(/),取余(%)的方法)
AC 代码
等个5秒才会输出;;提交时直接cout
#include
using namespace std;
int ans, fir, sec, cnt; //fir前半段, sec后半段, cnt当前第几位
//判断位数
int lo(int x)
{
int len = 0;
while(x) {
len++;
x /= 10;
}
return len;
}
//判断前半和后半数字相加和
void cal(int x)
{
int y = x;
while(cnt< lo(y) / 2) {
fir += x % 10;
cnt++;
x /= 10;
}
while(cnt < lo(y)) {
sec += x % 10;
cnt++;
x /= 10;
}
}
int main()
{
for(int i = 1; i <= 100000000; ++i) {
fir = 0, sec = 0, cnt = 0;
cal(i); //得到first和second的值
if(fir == sec && lo(i) % 2 == 0) { //偶数且前半 = 后半
ans++;
}
}
cout< 4430091代码2 知识点
to_stirng应该也能做,只是代码跑了5分钟没跑出来,就给删了
数字常量(整型,浮点型)转化位字符串,需要用到to_string函数
如果是 ' ' 里面是单个字符,返回对应的ASCII值
(9条消息) C++ to_string()函数_WeSiGJ的博客-CSDN博客
#include
using namespace std;
int main()
{
string b = to_string('5');
cout< 53
12.523400
97
97B,2068: [蓝桥杯2023初赛] 有奖问答
P2068 - [蓝桥杯2023初赛] 有奖问答 - New Online Judge (ecustacm.cn)
标签:基础题,深度优先搜索,组合数学
当时就写了dfs,还错了
先分享一下组合数学的知识,虽然本题不知道哪里用了组合数学
组合数学(来源于Oi-Wiki)
AC DFS
详情看注释
#include
using namespace std;
int ans;
void dfs(int step, int score)
{
// == 70要放在==100和return;前
if(score == 70) ans++; //此时不需要return;
//30题答完或分数达到100
if(step == 31 || score == 100) return;
//分治递归
dfs(step + 1, score + 10); //答对
dfs(step + 1, 0); //答错
}
int main()
{
dfs(1, 0); //第1题, 分数0开始
cout< 跑个5秒出答案
8335366DP的方法
本题用dp的话,时间和空间复杂度都是线性的,效率高,适用于大规模数据的计算
思路
这里我们将每10分变成1分,70分变成7分,100分变成10分,便于计算
1,状态确定
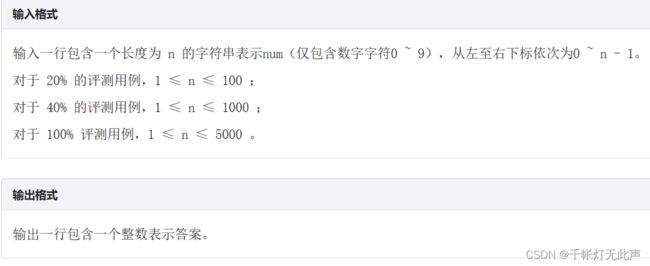
dp[i][j]表示第 i 题拿到 j 分的方案数,30题最多100分 --> 10分,我们声明 int dp[40][20];
2,递推式
(1)
由于答错一题就归零,不论前面情况如何,7分时,这7分前面一定是 ***** + 错
(此处*****代表所有情况)(所以答错一题就继承上一题所有分数的方案数和)
然后连续7题答对,是一种方案数,dp[i][0] += dp[i - 1][j] (+=是因为,注意看前面描述,“前面所有情况,就是第i - 1题所有得分情况的方案数的和才是dp[i][0]的方案数,所以是+=”)
(2)
dp[i][j] = dp[i - 1][j - 1] 则表示第i题答对了,+10分并继承上一题的方案数
3,初始化
由递推式推初始状态,显然,除了dp[0][0]为1,其余设置为0
因为dp[i][0]表示二维矩阵第1列,也就是每一行第一个都是由上面一行相加得到
而dp[i][j]表示当 j != 0 时,都是由左上角(i - 1, j - 1)的值得到
dp[0][0] = 1,表示未开始答题且得分为0时,方案数只有1种
特别解释下代码第10,12行
第10行,if(j != 10),因为dp[i][10]会继承dp[i - 1][9]的数据,当分数为100时,会自动停止答题,所以dp[i][10]都应该设为0,如果不用if(j != 10),第一列的dp[i][0]就会加上上一行第10列的值,进而增大了后面dp[i][7]的值,结果就会偏大
第12行,j != 0为了不超限
AC DP
#include
using namespace std;
int dp[40][20], ans; //答对一题+1分
int main()
{
dp[0][0] = 1; //初始化
for(int i = 1; i <= 30; ++i) //30题
for(int j = 0; j <= 10; ++j) {//100分
if(j != 10) //否则j = 10时会得到左上角的方案数
dp[i][0] += dp[i - 1][j];
if(j != 0)
dp[i][j] = dp[i - 1][j - 1];
}
//遍历每一题70分的方案数加起来
for(int i = 0; i <= 30; ++i)
ans += dp[i][7];
cout< 8335366C,2069: [蓝桥杯2023初赛] 平方差
P2069 - [蓝桥杯2023初赛] 平方差 - New Online Judge (ecustacm.cn)
标签:基础题,数论
AC 28% 暴力
暴力
#include
using namespace std;
int ans;
int main()
{
int l, r;
cin>>l>>r;
for(int k = l; k <= r; ++k) {
int flag = 0;
for(int i = 1; i < 3000; ++i) {
for(int j = 0; j < i; ++j) {
if(i*i - j*j == k) {
flag = 1;
ans++;
break; //每满足一次, k就自增
}
//剪枝
if(i*i - (i-1)*(i-1) > k) break;
}
if(flag) break; //防止ans重复自增
}
}
cout< 找规律
隔1个数
“容易”发现1,3,5,7,9......来源于1^2 - 0^2 == 1,2^2 - 1^2 == 3,3^2 - 2^2 == 5......
也就是隔一个数的平方差可以得到所有奇数
隔2个数
“容易”发现4的倍数来源于m的平方 - (m - 2)的平方,比如2^2 - 0^2 == 4或者
3^2 - 1^2 == 8或者4^2 - 2^2 == 12...
也就是隔两个数的平方差可以得到所有4的倍数
再一观察,除了2的倍数外,是不是齐活了?
因为所有大于0的(奇数 + 偶数)等于所有正数(题目中1 <= L <= R)
然后目前得到了所有奇数 + 所有4的倍数
所以满足这个条件的x一定是奇数或者4的倍数
AC 92% O(n)
数据量高达1e9,显然就算O(n)也会超时
#include
using namespace std;
int main()
{
int l, r, ans = 0;
cin>>l>>r;
for(int i = l; i <= r; ++i) {
if(i % 2 == 1) ans++; //奇数
else if(i % 4 == 0) ans++; //4的倍数
}
cout< AC 100% O(1)
转化为求[left, right]之间,是2的倍数不是4的倍数的个数ans(wer),也就是2倍数的个数 - 4倍数的个数
再用[l, r]的个数(r - l + 1)减去ans即可O(1),也就不用遍历了
额外的测试
2 19
9 4
13
3 19
8 4
13
4 19
8 4
12
2 20
10 5
14AC 代码
#include
using namespace std;
int main()
{
int l, r, ans = 0; //ans为不满足的条件
cin>>l>>r;
int x = r / 2 - (l-1) / 2; //2的倍数
int y = r / 4 - (l-1) / 4; //4的倍数
ans = x - y; //不满足条件
//cout< D,2070: [蓝桥杯2023初赛] 更小的数
P2070 - [蓝桥杯2023初赛] 更小的数 - New Online Judge (ecustacm.cn)
当时也不会,只能用s.substr做了,所幸还挺好做
功能:截取子串
s.substr(i)从下标 i 开始到结尾,s.substr(i, j)从下标 i 开始截取 j 个字符
#include //s.substr()
string s1 = s.substr(j, i); //下标j开始, 截取i个字符
string s2 = s.substr(i); //下标i开始,截取到末尾 AC 44% s.substr
比赛时的代码 --> 时间超限
#include
using namespace std;
int ans;
string s2, s3; //全局变量
//字符串反向函数
void rever()
{
for(int i = s2.size() - 1; i >= 0; --i)
s3 += s2[i];
}
int main()
{
string s;
cin>>s;
for(int i = 0; i < s.size() - 1; ++i)
for(int j = 2; i + j <= s.size(); ++j) {
s2 = s.substr(i, j); //原子串
s3 = ""; //初始化新子串
rever(); //反向
if(s3 < s2) ans++;
}
cout< DP 做法
实际上是区间dp,还没学,但是!dp都一个鸟样,把四部曲分析清楚就行
(虽然大多数时候连状态都确定不了,或者状态确定了,递推式不会推)
思路
由题目,一个子串反转能否s_new < s,只需要对子串长度和左端下标进行遍历
(这就和substr的想法有点像,不过substr每次都要重新比较每一个位置的字符,所以效率低,而动规直接继承子问题的数据)
右端下标可有长度和左端下标得出(由题目,显然长度>=2)
1,
如果发现左端字符大于右端,显然这部分子串可以反转,方案数为1
2,
如果等于,就继续往中间遍历,且方案数等于下一个下标处的方案数
3,
如果小于,方案数为0
显然,子问题重叠,且子问题的最优解能代表整个问题的最优解,当然用动规
然后注意到数据量达5000,“众所周知”,32位int全局变量开二维数组,最大约dp[5050][5050]
直接想到了二维dp,当然如果数据量增大到1e5
后续需要转一维,而能否“滚动数组”,压到一维,看“当前层是否都由上一层推导过来的”
dp四部曲
1,状态
dp[l][r]表示区间[l, r]的子串,也就是子串左端下标为l(eft),右端下标为r(ight)
2,递推式
(1)
if(s[l] > s[r]) dp[l][r] = 1; 表示左端字符 < 右端字符,由于从外向中间遍历,在这个特定的长度和左右下标下,反转满足方案数为1
(2)
if(s[l] == s[r]) dp[l][r] = dp[l + 1][r - 1],向里遍历,此时判断不出反转后是否满足要求,是否满足取决于下一步
(3)
if(s[l] > s[r]) dp[l][r] = 0,这步可省略,全局变量已经初始化为0
3,初始化
考虑到 len(子串长度 len>=2)所以dp[l + 1][r - 1]中的r - 1并不会越界,因为r = l + len - 1
无需特别初始化
4,遍历方向
一般二维怎么都行,一维得逆序遍历
AC DP
#include
using namespace std;
int dp[5010][5010], ans;
int main()
{
string s;
cin>>s;
int n = s.size();
for(int len = 2; len <= n; ++len) { //len子串长度
for(int l = 0; l + len <= n; ++l) { //l子串左端下标
int r = l + len - 1; //右端下标
if(s[l] > s[r]) dp[l][r] = 1;
else if(s[l] == s[r]) dp[l][r] = dp[l + 1][r - 1];
ans += dp[l][r];
}
}
cout< AC 常规
2层for循环遍历,同时,遇到可以翻转的情况,开始逐层向外遍历,出现连续的字符相等的情况,也算一种方案数
#include
using namespace std;
int main()
{
string s;
cin>>s;
int n = s.size(), ans = 0;
//遍历
for(int i = 0; i < n; ++i)
for(int j = i + 1; j < n; ++j) {
if(s[i] <= s[j]) continue;
ans++; //反转符合要求
//翻转后, 外层连续的相等也符合
for(int k = 1; i - k >= 0 && j + k < n; ++k) {
if(s[i - k] == s[j + k]) //由里向外遍历
ans++;
else
break; //剪枝
}
}
cout< E,2071: [蓝桥杯2023初赛] 颜色平衡树
标签:进阶题,启发式合并
比赛时暴力了,下面我展示当时暴力的代码和AC代码
AC代码主要2种,一是并查集路径压缩 + 按秩合并,而是启发式合并(dsu on tree)
启发式合并有模板的
AC 9% 暴力
15 * 0.09 = 1.35(时间超限),四舍五入 = 1分????考场上就1分
#include
#include //scanf()
#include //sort()
#include //memset()
using namespace std;
int vis[200010];
struct node
{
int color, fa; //颜色和父节点
}a[200010];
bool cmp(node x, node y)
{
return x.fa < y.fa; //按父节点从小到大排序
}
int main()
{
int n, ans = 0;
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%d%d", &a[i].color, &a[i].fa);
sort(a, a + n, cmp);
//暴力每个节点的子树
for(int i = 0; i < n; ++i) {
int u = 0, flag = 1;
memset(vis, 0, sizeof(vis));
for(int j = i; j < n; ++j) {
vis[a[j].color]++;
u = max(u, a[j].color); //出现过颜色中的最大值
}
for(int k = 1; k <= u; ++k)
if(vis[k] != 0 && vis[k] != vis[u]) {
flag = 0;
break;
}
if(flag) ans++;
}
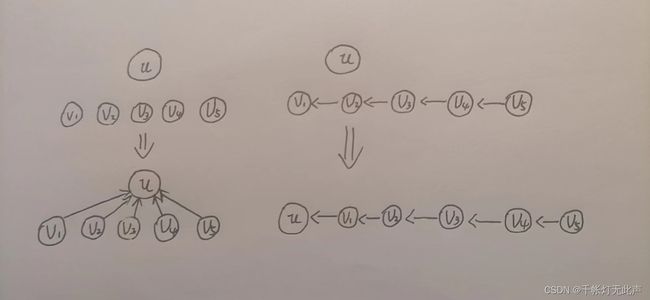
cout< 关于为什么用启发式合并,而不是直接暴力,比如
如果是第一种情况,暴力也没问题,但是第二种情况
让大的集合向小的集合合并,时间复杂度就会很高
知识点
下面讲讲启发式合并
→ 树上启发式合并 - OI Wiki (oi-wiki.org)
→ 并查集复杂度 - OI Wiki (oi-wiki.org)
→ DSU on Tree入门 - TheLostWeak - 博客园 (cnblogs.com)
→ (18条消息) 并查集(按秩合并+路径压缩)基础讲解_并查集按秩合并_夜幕而已的博客-CSDN博客
每次合并时,都将较少元素的集合合并至较多元素的集合
当一个元素转移到另一个集合,新集合的大小至少是原集合2倍
所以一个元素最多被插入logn次,单个元素对时间复杂度的贡献为O(logn)
n个元素的时间复杂度就为O(nlogn)
补充
1,子节点:根节点以外的其他节点
2,重儿子:子节点重,子树大小最大的节点
代码实现
最常见的是并查集的按秩合并,元素少的集合合并到元素多的集合上,以减少树的深度
其中秩指的是以某个节点为根的子树的深度,或者说高度
const int N = 10010;
int dad[N], deep[N];
//初始化
void init()
{
for(int i = 0; i < N; ++i) {
dad[i] = i; //自己是自己的爸爸
deep[i] = 1; //初始深度都是1
}
}
//找爸爸
int Find(int x)
{
if(x != dad[x])
return dad[x] = Find(dad[x]); //记得return
}
//合并
void join(int x, int y)
{
int xx = Find(x), yy = Find(y);
if(xx != yy) {
if(deep[xx] > deep[yy])
dad[yy] = xx; //xx更大
else {
dad[xx] = yy; //yy更大
if(deep[xx] == deep[yy])
deep[xx]++; //随便一个深度+1
}
}
Find(yy); //路径压缩优化
}解释
疑问1:为什么每次深度只+1呢,如果深度多了更多,不应该加更多吗?
按秩合并算法中deep[]记录的不是节点所在树的实际深度,而是根据当前节点的子树大小估计出来的一个“秩”(rank),用于优化合并操作的效率
具体就是,deep[]越大,其子树包含的节点数越多
这里有道(启发式 或 按秩)合并都能做的例题,先放这了
P3201 [HNOI2009] 梦幻布丁 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
不挣扎了,作业4天没写了,今晚2个ddl,下午还得足球裁判,晚上3节线代,先这样吧!
AC 按秩合并
bla...AC 启发式合并
bla...