第五章 RNN
目录
- 5.1 概率和语言模型
-
- 5.1.1 概率视角下的 word2vec
- 5.1.2 语言模型
- 5.1.3 将CBOW模型用作语言模型?
- 5.2 RNN
-
- 5.2.1 循环的神经网络
- 5.2.2 展开循环
- 5.2.3 Backpropagation Through Time
- 5.2.4 Truncated BPTT
- 5.2.5 Truncated BPTT的mini-batch学习
- 5.3 RNN的实现
-
- 5.3.1 RNN层的实现
- 5.3.2 Time RNN层的实现
- 5.4 处理时序数据的层的实现
-
- 5.4.1 RNNLM的全貌图
- 5.4.2 Time层的实现
- 5.5 RNNLM的学习和评价
-
- 5.5.1 RNNLM的实现
- 5.5.2 语言模型的评价
- 5.5.3 RNNLM的学习代码
- 5.5.4 RNNLM的Trainer类
到目前为止, 我们看到的神经网络都是前馈型神经网络。前馈(feedforward)是指网络的传播方向是单向的。具体地说,先将输入信号传给下一层(隐藏层),接收到信号的层也同样传给下一层,然后再传给下一 层 … … \dots \dots ……像这样,信号仅在一个方向上传播。
虽然前馈网络结构简单、易于理解,但是可以应用于许多任务中。不过, 这种网络存在一个大问题,就是不能很好地处理时间序列数据(以下简称为 “时序数据”)。更确切地说,单纯的前馈网络无法充分学习时序数据的性质(模式)。于是,RNN(Recurrent Neural Network,循环神经网络)便应运而生。
5.1 概率和语言模型
5.1.1 概率视角下的 word2vec
考虑由单词序列 w 1 , w 2 , … , w T w_1, w_2, \dots , w_T w1,w2,…,wT 表示的语料库,将第 t t t 个单词作为目标词,将它左右的 (第 t − 1 t − 1 t−1 个和第 t + 1 t + 1 t+1 个)单词作为上下文。如图 5-1 所示,CBOW 模型所做的事情就是从上下文( w t − 1 w_{t−1} wt−1 和 w t + 1 w_{t+1} wt+1) 预测目标词( w t w_t wt)。
下面,我们用数学式来表示 “当给定 w t − 1 w_{t−1} wt−1 和 w t + 1 w_{t+1} wt+1 时目标词是 w t w_t wt 的概率”,如下式所示:
P ( w t ∣ w t − 1 , w t + 1 ) P(w_t|w_{t-1},w_{t+1}) P(wt∣wt−1,wt+1)
CBOW 模型对式 (5.1) 这一后验概率进行建模。这个后验概率表示 “当给定 w t − 1 w_{t−1} wt−1 和 w t + 1 w_{t+1} wt+1 时 w t w_t wt 发生的概率”。这是窗口大小为 1 1 1 时的 CBOW 模型。 顺便提一下,我们之前考虑的窗口都是左右对称的。这里我们将上下文限定为左侧窗口,比如图 5-2 所示的情况。
在仅将左侧 2 个单词作为上下文的情况下,CBOW 模型输出的概率如 式 (5.2) 所示:
P ( w t ∣ w t − 2 , w t − 1 ) P(w_t|w_{t-2}, w_{t-1}) P(wt∣wt−2,wt−1)
使用上式的写法,CBOW 模型的损失函数可以写成下式。下式是从交叉熵误差推导出来的结果。
L = − l o g P ( w t ∣ w t − 2 , w t − 1 ) L = -log\ P(w_t|w_{t-2}, w_{t-1}) L=−log P(wt∣wt−2,wt−1)
CBOW 模型的学习旨在找到使上式表示的损失函数(确切地说, 是整个语料库的损失函数之和)最小的权重参数。只要找到了这样的权重参数,CBOW 模型就可以更准确地从上下文预测目标词。
CBOW 模型的学习目的是从上下文预测出目标词,随着学习的推进,(作为副产品)获得了编码了单词含义信息的单词的分布式表示。
那么,CBOW 模型本来的目的 “从上下文预测目标词” 是否可以用来做些什么呢?上式表示的概率 P ( w t ∣ w t − 2 , w t − 1 ) P(w_t|w_{t-2}, w_{t-1}) P(wt∣wt−2,wt−1) 是否可以在一些实际场景中发挥作用呢?说到这里,就要提一下语言模型了。
5.1.2 语言模型
语言模型(language model)给出了单词序列发生的概率。具体来说, 就是使用概率来评估一个单词序列发生的可能性,即在多大程度上是自然的单词序列。比如,对于 “you say goodbye” 这一单词序列,语言模型给出高概率(比如 0.092);对于 “you say good die” 这一单词序列,模型则给出低概率(比如 0.000 000 000 003 2)
语言模型可以应用于多种应用,典型的例子有机器翻译和语音识别。比如,语音识别系统会根据人的发言生成多个句子作为候选。此时,使用语言模型,可以按照 “作为句子是否自然” 这一基准对候选句子进行排序。
语言模型也可以用于生成新的句子。因为语言模型可以使用概率来评价单词序列的自然程度,所以它可以根据这一概率分布造出(采样)单词。
现在,我们使用数学式来表示语言模型。这里考虑由 m m m 个单词 w 1 , … , w m w_1, \dots , w_m w1,…,wm 构成的句子,将单词按 w 1 , … , w m w_1, \dots , w_m w1,…,wm 的顺序出现的概率记为 P ( w 1 , … , w m ) P(w_1, \dots , w_m) P(w1,…,wm)。因为这个概率是多个事件一起发生的概率,所以称为联合概率。
使用后验概率可以将这个联合概率 P ( w 1 , … , w m ) P(w_1, \dots , w_m) P(w1,…,wm) 分解成如下形式:
P ( w 1 , … , w m ) = P ( w m ∣ w 1 , … , w m − 1 ) P ( w m − 1 ∣ w 1 , … , w m − 2 ) … P ( w 3 ∣ w 1 , w 2 ) P ( w 2 ∣ w 1 ) P ( w 1 ) = ∏ t = 1 m P ( w t ∣ w 1 , … , w t − 1 ) \begin{align} P(w_1, \dots, w_m) &= P(w_m|w_1, \dots, w_{m-1})P(w_{m-1}|w_1, \dots, w_{m-2})\dots P(w_3|w_1,w_2)P(w_2|w_1)P(w_1) \\ &=\prod_{t=1}^m P(w_t|w_1, \dots, w_{t-1}) \end{align} P(w1,…,wm)=P(wm∣w1,…,wm−1)P(wm−1∣w1,…,wm−2)…P(w3∣w1,w2)P(w2∣w1)P(w1)=t=1∏mP(wt∣w1,…,wt−1)
如上式所示,联合概率 P ( w 1 , … , w m ) P(w_1, \dots , w_m) P(w1,…,wm) 可以表示为后验概率的乘积 ∏ P ( w t ∣ w 1 , … , w t − 1 ) \prod P(w_t|w_1, \dots , w_{t−1}) ∏P(wt∣w1,…,wt−1)。这里需要注意的是,这个后验概率是以目标词左侧的全部单词为上下文(条件)时的概率,如图 5-3 所示。
这里我们来总结一下,我们的目标是求 P ( w t ∣ w 1 , … , w t − 1 ) P(w_t|w_1, \dots , w_{t−1}) P(wt∣w1,…,wt−1) 这个概率。 如果能计算出这个概率,就能求得语言模型的联合概率 P ( w 1 , … , w m ) P(w_1, \dots , w_m) P(w1,…,wm)。
P ( w t ∣ w 1 , … , w t − 1 ) P(w_t|w_1, \dots , w_{t−1}) P(wt∣w1,…,wt−1) 表示的模型称为条件语言模型(conditional language model),有时也将其称为语言模型。
5.1.3 将CBOW模型用作语言模型?
那么,如果要把 word2vec 的 CBOW 模型(强行)用作语言模型,该怎么办呢?可以通过将上下文的大小限制在某个值来近似实现,用数学式可以如下表示:
P ( w 1 , … , w m ) = ∏ t = 1 m P ( w t ∣ w 1 , … , w t − 1 ) ≈ ∏ t = 1 m P ( w t ∣ w t − 2 , w t − 1 ) P(w_1, \dots, w_m) =\prod_{t=1}^m P(w_t|w_1, \dots, w_{t-1}) \approx \prod_{t=1}^m P(w_t|w_{t-2},\ w_{t-1}) P(w1,…,wm)=t=1∏mP(wt∣w1,…,wt−1)≈t=1∏mP(wt∣wt−2, wt−1)
这里,我们将上下文限定为左侧的 2 个单词。如此一来,就可以用 CBOW 模型(CBOW 模型的后验概率)近似表示。
在机器学习和统计学领域,经常会听到 “马尔可夫性”(或者“马尔可夫模型”“马尔可夫链”)这个词。马尔可夫性是指未来的状态仅依存于当前状态。此外,当某个事件的概率仅取决于其前面的 N 个 事件时,称为“N阶马尔可夫链”。这里展示的是下一个单词仅取决 于前面 2 个单词的模型,因此可以称为 “2阶马尔可夫链”。
上式是使用 2 个单词作为上下文的例子,但是这个上下文的大小可以设定为任意长度(比如 5 或 10)。不过,虽说可以设定为任意长度,但必须是某个“固定”长度。比如,即便是使用左侧 10 个单词作为上下文的 CBOW 模型,其上下文更左侧的单词的信息也会被忽略,而这会导致问题, 如图 5-4 中的例子所示。
在图 5-4 的问题中,“Tom 在房间看电视,Mary 进了房间”。根据该语境(上下文),正确答案应该是 Mary 向 Tom(或者“him”)打招呼。这里要获得正确答案,就必须将 “?” 前面第 18 个单词处的 Tom 记住。如果 CBOW 模型的上下文大小是 10,则这个问题将无法被正确回答。
那么,是否可以通过增大 CBOW 模型的上下文大小(比如变为 20 或 30)来解决此问题呢?的确,CBOW 模型的上下文大小可以任意设定,但是 CBOW 模型还存在忽视了上下文中单词顺序的问题。
CBOW 是 Continuous Bag-Of-Words 的简称。Bag-Of-Words 是 “一袋子单词” 的意思,这意味着袋子中单词的顺序被忽视了。
关于上下文的单词顺序被忽视这个问题,我们举个例子来具体说明。比如,在上下文是 2 个单词的情况下,CBOW 模型的中间层是那 2 个单词向量的和,如图 5-5 所示。
如图 5-5 的左图所示,在 CBOW 模型的中间层求单词向量的和,因此上下文的单词顺序会被忽视。比如,(you, say) 和 (say, you) 会被作为相同的内容进行处理。
我们想要的是考虑了上下文中单词顺序的模型。为此,可以像图 5-5 中 的右图那样,在中间层“拼接”(concatenate)上下文的单词向量。但是,如果采用拼接的方法,权重参数的数量将与上下文大小成比例地增加。显然,这是我们不愿意看到的。
这里,RNN 具有一个机制,那就是无论上下文有多长,都能将上下文信息记住。因此,使用 RNN 可以处理任意长度的时序数据。
word2vec 是以获取单词的分布式表示为目的的方法,因此一般不会用于语言模型。这里,为了引出 RNN 的魅力,我们拓展了话题,强行将 word2vec 的 CBOW 模型应用在了语言模型上。
5.2 RNN
RNN(Recurrent Neural Network)中的 Recurrent 源自拉丁语,意思是 “反复发生”,可以翻译为 “重复发生” “周期性地发生” “循环”,因此 RNN 可以直译为 “复发神经网络” 或者 “循环神经网络”。
Recurrent Neural Network 通常译为“循环神经网络”。另外, 还有一种被称为 Recursive Neural Network(递归神经网络)的网络。这个网络主要用于处理树结构的数据,和循环神经网络不是一个东西。
5.2.1 循环的神经网络
“循环”是什么意思呢?是 “反复并持续” 的意思。从某个地点出发, 经过一定时间又回到这个地点,然后重复进行,这就是“循环”一词的含 义。这里要注意的是,循环需要一个“环路”。
只有存在了“环路”或者“回路”这样的路径,媒介(或者数据)才能在相同的地点之间来回移动。随着数据的循环,信息不断被更新。
RNN 的特征就在于拥有这样一个环路(或回路)。这个环路可以使数据不断循环。通过数据的循环,RNN 一边记住过去的数据,一边更新到最新的数据。
下面,我们来具体地看一下 RNN。这里,我们将 RNN 中使用的层称为“RNN 层”,如图 5-6 所示。
如图 5-6 所示,RNN 层有环路。通过该环路,数据可以在层内循环。 在图 5-6 中,时刻 t t t 的输入是 x t x_t xt,这暗示着时序数据 ( x 0 , x 1 , … , x t , … ) (x_0, x_1, \dots , x_t, \dots) (x0,x1,…,xt,…) 会被输入到层中。然后,以与输入对应的形式,输出 ( h 0 , h 1 , … , h t , … ) (h_0, h_1, \dots , h_t, \dots) (h0,h1,…,ht,…)。
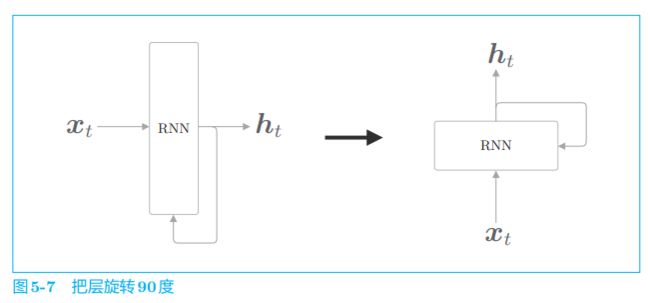
接着,我们来详细介绍一下图 5-6 的循环结构。在此之前,我们先将 RNN 层的绘制方法更改如下。
如图 5-7 所示,到目前为止,我们在绘制层时都是假设数据从左向右流动的。不过,从现在开始,为了节省纸面空间,我们将假设数据是从下向上流动的(这是为了在之后需要展开循环时,能够在左右方向上将层铺开)。
5.2.2 展开循环
如图 5-8 所示,通过展开 RNN 层的循环,我们将其转化为了从左向右延伸的长神经网络。这和我们之前看到的前馈神经网络的结构相同(前馈网络的数据只向一个方向传播)。不过,图 5-8 中的多个 RNN 层都是 “同一 个层”,这一点与之前的神经网络是不一样的。
时序数据按时间顺序排列。因此,我们用 “时刻” 这个词指代时序数据的索引(比如,时刻 t t t 的输入数据为 x t x_t xt)。在自然语言处理的情况下,既使用 “第 t t t 个单词” “第 t t t 个 RNN 层” 这样的表述, 也使用 “时刻 t t t 的单词” 或者 “时刻 t t t 的 RNN 层” 这样的表述。
由图 5-8 可以看出,各个时刻的 RNN 层接收传给该层的输入和前一个 RNN 层的输出,然后据此计算当前时刻的输出,此时进行的计算可以用下式表示:
h t = t a n h ( h t − 1 W h + x t W x + b ) h_t = tanh(h_{t-1}W_h \ + \ x_tW_x \ + \ b) ht=tanh(ht−1Wh + xtWx + b)
RNN 有两个权重,分别是将输入 x x x 转化为输出 h h h 的权重 W x W_x Wx 和将前一个 RNN 层的输出转化为当前时刻的输出的权重 W h W_h Wh。此外,还有偏置 b b b。这里, h t − 1 h_{t−1} ht−1 和 x t x_t xt 都是行向量。
在上式 中,首先执行矩阵的乘积计算,然后使用 t a n h tanh tanh 函数(双曲正切函数)变换它们的和,其结果就是时刻 t t t 的输出 h t h_t ht。这个 h t h_t ht 一方面向上输出到另一个层,另一方面向右输出到下一个 RNN 层(自身)。
观察上式可以看出,现在的输出 h t h_t ht 是由前一个输出 h t − 1 h_{t−1} ht−1 计算出来的。从另一个角度看,这可以解释为,RNN 具有 “状态” h h h,并以上式的形式被更新。这就是说 RNN 层是 “具有状态的层” 或 “具有存储(记忆)的层” 的原因。
RNN 的 h h h 存储 “状态”,时间每前进一步(一个单位),它就以上式的形式被更新。许多文献中将 RNN 的输出 h t h_t ht 称为隐藏状态(hidden state)或隐藏状态向量(hidden state vector)。
5.2.3 Backpropagation Through Time
将 RNN 层展开后,就可以视为在水平方向上延伸的神经网络,因此 RNN 的学习可以用与普通神经网络的学习相同的方式进行,如图 5-10 所示。
如图 5-10 所示,将循环展开后的 RNN 可以使用(常规的)误差反向传播法。换句话说,可以通过先进行正向传播,再进行反向传播的方式求目标梯度。因为这里的误差反向传播法是 “按时间顺序展开的神经网络的误差反向传播法”,所以称为 Backpropagation Through Time(基于时间的反向传播),简称 BPTT。
通过该 BPTT,RNN 的学习似乎可以进行了,但是在这之前还有一个必须解决的问题,那就是学习长时序数据的问题。因为随着时序数据的时间跨度的增大,BPTT 消耗的计算机资源也会成比例地增大。另外,反向传播的梯度也会变得不稳定。
要基于 BPTT 求梯度,必须在内存中保存各个时刻的 RNN 层的中间数据(RNN 层的反向传播将在后文中说明)。因此,随着时序数据变长,计算机的内存使用量(不仅仅是计算量)也会增加。
5.2.4 Truncated BPTT
在处理长时序数据时,通常的做法是将网络连接截成适当的长度。具体来说,就是将时间轴方向上过长的网络在合适的位置进行截断,从而创建多个小型网络,然后对截出来的小型网络执行误差反向传播法,这个方法称为 Truncated BPTT(截断的 BPTT)。
在 Truncated BPTT 中,网络连接被截断,但严格地讲,只是网络的反向传播的连接被截断,正向传播的连接依然被维持,这一点很重要。也就是说,正向传播的信息没有中断地传播。与此相对,反向传播则被截断为适当的长度,以被截出的网络为单位进行学习。
现在,我们结合具体的例子来介绍 Truncated BPTT。假设有一个长度为 1000 的时序数据。在自然语言处理的情况下,这相当于一个有 1000 个单词的语料库。
在处理长度为 1000 的时序数据时,如果展开 RNN 层,它将成为在水平方向上排列有 1000 个层的网络。当然,无论排列多少层,都可以根据误差反向传播法计算梯度。但是,如果序列太长,就会出现计算量或者内存使用量方面的问题。此外,随着层变长,梯度逐渐变小,梯度将无法向前一层传递。因此,如图 5-11 所示,我们来考虑在水平方向上以适当的长度截断网络的反向传播的连接。
在图 5-11 中,我们截断了反向传播的连接,以使学习可以以 10 个 RNN 层为单位进行。像这样,只要将反向传播的连接截断,就不需要再考虑块范围以外的数据了,因此可以以各个块为单位(和其他块没有关联)完成误差反向传播法。
这里需要注意的是,虽然反向传播的连接会被截断,但是正向传播的连接不会。因此,在进行 RNN 的学习时,必须考虑到正向传播之间是有关联的,这意味着必须按顺序输入数据。下面,我们来说明什么是按顺序输入 数据。
我们之前看到的神经网络在进行 mini-batch 学习时,数据都是随机选择的。但是,在 RNN 执行 Truncated BPTT 时,数据需要按顺序输入。
现在,我们考虑使用 Truncated BPTT 来学习 RNN。我们首先要做的是,将第 1 1 1 个块的输入数据 ( x 0 , … , x 9 ) (x_0, \dots , x_9) (x0,…,x9) 输入 RNN 层。这里要进行的处理如图 5-12 所示。
如图 5-12 所示,先进行正向传播,再进行反向传播,这样可以得到所需的梯度。接着,对下一个块的输入数据 ( x 10 , x 11 , … , x 19 ) (x_{10}, x_{11}, \dots , x_{19}) (x10,x11,…,x19) 执行误差反向传播法,如图 5-13 所示。
这里,和第 1 个块一样,先执行正向传播,再执行反向传播。这里的重点是,这个正向传播的计算需要前一个块最后的隐藏状态 h 9 h_9 h9,这样可以维持正向传播的连接。
用同样的方法,继续学习第 3 个块,此时要使用第 2 个块最后的隐藏状态 h 19 h_{19} h19。像这样,在 RNN 的学习中,通过将数据按顺序输入,从而继承隐藏状态进行学习。根据到目前为止的讨论,可知 RNN 的学习流程如图 5-14 所示。
如图 5-14 所示,Truncated BPTT 按顺序输入数据,进行学习。这样一来,能够在维持正向传播的连接的同时,以块为单位应用误差反向传播法。
5.2.5 Truncated BPTT的mini-batch学习
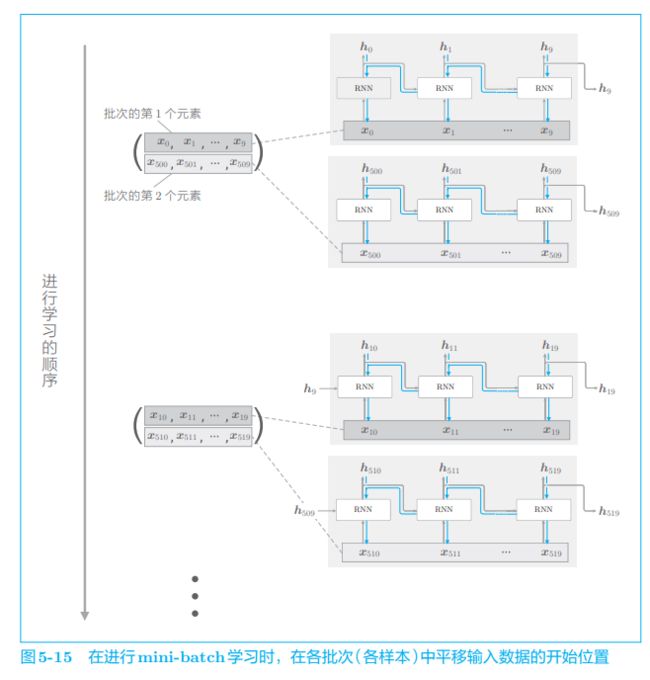
到目前为止,我们在探讨 Truncated BPTT 时,并没有考虑 minibatch 学习。换句话说,我们之前的探讨对应于批大小为 1 的情况。为了执行 mini-batch 学习,需要考虑批数据,让它也能像图 5-14 一样按顺序输入数据。因此,在输入数据的开始位置,需要在各个批次中进行 “偏移” 。
仍用上一节的通过 Truncated BPTT 进行学习的例子,对长度为 1000 的时序数据,以时间长度10为单位进行截断。此时,如何将批大小设为 2 进行学习呢?在这种情况下,作为 RNN 层的输入数据, 第 1 笔样本数据从头开始按顺序输入,第 2 笔数据从第 500 个数据开始按顺序输入。也就是说,将开始位置平移 500,如图 5-15 所示。
如图 5-15 所示,批次的第 1 个元素是 x 0 , … , x 9 x_0, \dots , x_9 x0,…,x9,批次的第 2 个元素是 x 500 , … , x 509 x_{500}, \dots , x_{509} x500,…,x509,将这个 mini-batch 作为 RNN 的输入数据进行学习。因 为要输入的数据是按顺序的,所以接下来是时序数据的第 $10 \sim 19 $个数据和第 510 ∼ 519 510 \sim 519 510∼519 个数据。像这样,在进行 mini-batch 学习时,平移各批次输入数据的开始位置,按顺序输入。此外,如果在按顺序输入数据的过程中遇到了结尾,则需要设法返回头部。
如上所述,虽然 Truncated BPTT 的原理非常简单,但是关于数据的输入方法有几个需要注意的地方。具体而言,一是要按顺序输入数据,二是要平移各批次(各样本)输入数据的开始位置。
5.3 RNN的实现
实际上,我们要实现的是一个在水平方向上延伸的神经网络。另外,考虑到基于 Truncated BPTT 的学习,只需要创建一个在水平方向上长度固定的网络序列即可,如图 5-16 所示。
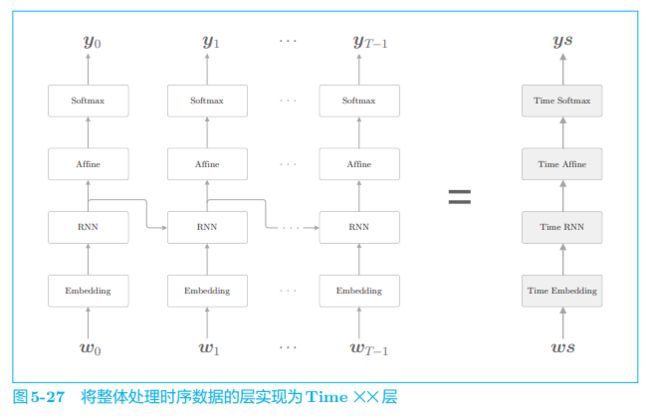
如图 5-16 所示,目标神经网络接收长度为 T T T 的时序数据( T T T 为任意值), 输出各个时刻的隐藏状态 T T T 个。这里,考虑到模块化,将图 5-16 中在水平方向上延伸的神经网络实现为“一个层”,如图 5-17 所示。
如图 5-17 所示,将垂直方向上的输入和输出分别捆绑在一起,就可以将水平排列的层视为一个层。换句话说,可以将 ( x 0 , x 1 , … , x T − 1 ) (x_0, x_1, \dots , x_{T−1}) (x0,x1,…,xT−1) 捆绑为 x s x_s xs 作为输入,将 ( h 0 , h 1 , … , h T − 1 ) (h_0, h_1, \dots , h_{T−1}) (h0,h1,…,hT−1) 捆绑为 h s h_s hs 作为输出。这里,我们将进行 Time RNN 层中的单步处理的层称为 “RNN 层”,将一次处理 T 步的层 称为“Time RNN 层”。
我们接下来进行的实现的流程是:首先,实现进行 RNN 单步处理的 RNN 类;然后,利用这个 RNN 类,完成一次进行 T T T 步处理的 TimeRNN 类。
5.3.1 RNN层的实现
见书
5.3.2 Time RNN层的实现
见书
5.4 处理时序数据的层的实现
将基于 RNN 的语言模型称为 RNNLM(RNN Language Model,RNN 语言模型)。
5.4.1 RNNLM的全貌图
图 5-25 所示为最简单的 RNNLM 的网络,其中左图显示了 RNNLM 的层结构,右图显示了在时间轴上展开后的网络。
图 5-25 中的第 1 层是 Embedding 层,该层将单词 ID 转化为单词的分布式表示(单词向量)。然后,这个单词向量被输入到 RNN 层。RNN 层向 下一层(上方)输出隐藏状态,同时也向下一时刻的 RNN 层(右侧)输出隐藏状态。RNN 层向上方输出的隐藏状态经过 Affine 层,传给 Softmax 层。
现在,我们仅考虑正向传播,向图 5-25 的神经网络传入具体的数据, 并观察输出结果。这里使用的句子还是我们熟悉的 “you say goodbye and i say hello.”,此时 RNNLM 进行的处理如图 5-26 所示。
如图 5-26 所示,被输入的数据是单词 ID 列表。首先,我们关注第 1 个 时刻。作为第 1 个单词,单词 ID 为 0 的 you 被输入。此时,查看 Softmax 层输出的概率分布,可知 say 的概率最高,这表明正确预测出了 you 后面出现的单词为 say。当然,这样的正确预测只在有“好的”(学习顺利的)权重时才会发生。
接着,我们关注第 2 个单词 say。此时,Softmax 层的输出在 goodbye 处和 hello 处概率较高。确实,“you say goodby”和“you say hello”都是很自然的句子(顺便说一下,正确答案是 goodbye)。这里需要注意的是, RNN 层 “记忆” 了 “you say” 这一上下文。更准确地说,RNN 将 “you say” 这一过去的信息保存为了简短的隐藏状态向量。RNN 层的工作是将这个信息传送到上方的 Affine 层和下一时刻的 RNN 层。
像这样,RNNLM 可以 “记忆” 目前为止输入的单词,并以此为基础预测接下来会出现的单词。RNN 层通过从过去到现在继承并传递数据,使得编码和存储过去的信息成为可能。
5.4.2 Time层的实现
之前我们将整体处理时序数据的层实现为了 Time RNN 层,这里也同样使用 Time Embedding 层、Time Affine 层等来实现整体处理时序数据的层。一旦创建了这些 Time 层,我们的目标神经网络就可以像图 5-27 这 样实现。
Time 层的实现很简单。比如,在 Time Affine 层的情况下,只需要像图 5-28 那样,准备 T 个 Affine 层分别处理各个时刻的数据即可。
Time Embedding 层也一样,在正向传播时准备 T 个 Embedding 层, 由各个 Embedding 层处理各个时刻的数据。
关于 Time Affine 层和 Time Embedding 层没有什么特别难的内容, 我们就不再赘述了。需要注意的是,Time Affine 层并不是单纯地使用 T 个 Affine 层,而是使用矩阵运算实现了高效的整体处理。
我们在 Softmax 中一并实现损失误差 Cross Entropy Error 层。这里, 按照图 5-29 所示的网络结构实现 Time Softmax with Loss 层。
图 5-29 中的 x 0 、 x 1 x_0、x_1 x0、x1 等数据表示从下方的层传来的得分(得分是正规化为概率之前的值), t 0 、 t 1 t_0、t_1 t0、t1 等数据表示正确解标签。如该图所示, T T T 个 Softmax with Loss 层各自算出损失,然后将它们加在一起取平均,将得到的值作为最终的损失。此处进行的计算可用下式表示:
L = 1 T ( L 0 + L 1 + ⋯ + L T − 1 ) L = \frac{1}{T}(L_0 + L_1 + \dots + L_{T-1}) L=T1(L0+L1+⋯+LT−1)
顺便说一下,这里的 Softmax with Loss 层计算 mini-batch 的平均损失。 具体而言,假设 mini-batch 有 N N N 笔数据,通过先求 N N N 笔数据的损失之和, 再除以 N N N,可以得到单笔数据的平均损失。这里也一样,通过取时序数据的平均,可以求得单笔数据的平均损失作为最终的输出。
5.5 RNNLM的学习和评价
5.5.1 RNNLM的实现
见书
5.5.2 语言模型的评价
语言模型基于给定的已经出现的单词(信息)输出将要出现的单词的概率分布。
困惑度(perplexity)常被用作评价语言模型的预测性能的指标。
简单地说,困惑度表示 “概率的倒数”(这个解释在数据量为 1 时严格一 致)。为了说明概率的倒数,我们仍旧考虑 “you say goodbye and i say hello.” 这一语料库。假设在向语言模型 “模型 1” 传入单词 you 时会输出图 5-32 的 左图所示的概率分布。此时,下一个出现的单词是 say 的概率为 0.8 0.8 0.8,这是一 个相当不错的预测。取这个概率的倒数,可以计算出困惑度为 1 0.8 = 1.25 \frac{1}{0.8} = 1.25 0.81=1.25。
而图 5-32 右侧的模型(“模型 2”)预测出的正确单词的概率为 0.2 0.2 0.2,这 显然是一个很差的预测,此时的困惑度为 1 0.2 = 5 \frac{1}{0.2}=5 0.21=5。
总结一下,“模型 1” 能准确地预测,困惑度是 1.25 1.25 1.25;“模型 2” 的预测未能命中,困惑度是 5.0 5.0 5.0。此例表明,困惑度越小越好。
那么,如何直观地解释值 1.25 1.25 1.25 和 5.0 5.0 5.0 呢?它们可以解释为 “分叉度”。 所谓分叉度,是指下一个可以选择的选项的数量(下一个可能出现的单词的候选个数)。在刚才的例子中,好的预测模型的分叉度是 1.25 1.25 1.25,这意味着下 一个要出现的单词的候选个数可以控制在 1 1 1 个左右。而在差的模型中,下一 个单词的候选个数有 5 5 5 个。
如上面的例子所示,基于困惑度可以评价模型的预测性能。好的模型可以高概率地预测出正确单词,所以困惑度较小(困惑度的最小 值是 1.0 1.0 1.0);而差的模型只能低概率地预测出正确单词,困惑度较大。
以上都是输入数据为 1 个时的困惑度。那么,在输入数据为多个的情况下,可以根据下面的式子进行计算。
L = − 1 N ∑ n ∑ k t n k l o g y n k 困惑度 = e L \begin{align} L &= -\frac{1}{N} \sum_n \sum_k t_{nk}\ logy_{nk}\\ 困惑度 &= e^L \end{align} L困惑度=−N1n∑k∑tnk logynk=eL
这里,假设数据量为 N N N 个。 t n t_n tn 是 one-hot 向量形式的正确解标签, t n k t_{nk} tnk 表 示第 n n n 个数据的第 k k k 个值, y n k y_{nk} ynk 表示概率分布(神经网络中的 Softmax 的输出)。顺便说一下, L L L 是神经网络的损失,使用这个 L L L 计算出的 e L e^L eL 就是困惑度。
在信息论领域,困惑度也称为 “平均分叉度”。这可以解释为,数据量为 1 时的分叉度是数据量为 N N N 时的分叉度的平均值。
5.5.3 RNNLM的学习代码
见书
5.5.4 RNNLM的Trainer类
见书