代码随想录算法训练营第五十九天 | 503.下一个更大元素II、42. 接雨水

打卡第59天，继续单调栈。

今日任务

• 503.下一个更大元素II
• 42.接雨水

503.下一个更大元素II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

提示:

• 1 <= nums.length <= 104
• -109 <= nums[i] <= 109

我的题解

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        vector<int> nums1(nums.begin(), nums.end());
        nums.insert(nums.end(), nums1.begin(), nums1.end());

        vector<int> res(nums.size(), -1);
        stack<int> st;
        for(int i = nums.size() - 1; i >= 0; i--) {
            while(!st.empty() && st.top() <= nums[i]) st.pop();
            if(!st.empty()) res[i] = st.top();
            st.push(nums[i]);
        }
        // 最后再把结果集即result数组resize到原数组大小
        res.resize(nums.size() / 2);
        return res;
    }
};

=## 42.接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

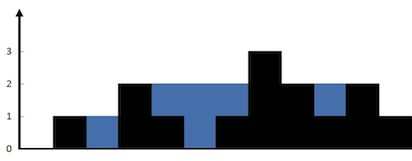
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

代码随想录

看了卡哥 的题解：使用单调栈，使得栈内元素单调递减，当前柱子高度大于（或等于${}^{[1]}$）栈顶柱子高度，栈顶柱子 为 接水的容器 底面，栈顶下一个元素是 接水的容器 的左侧，当前柱子接水的容器 的右侧， 容器宽度 w 等于 左右侧举例， 高度 h 等于 左右侧最短柱与地面柱子 的高度差，体积 $w\ast h$。

$[1]$ : 当前柱子高度等于栈顶柱子高度，要更新栈顶，当有两根一样的柱子其实是右边那根柱子充当下一个容器壁。为什么直接就height[st.top()] <= height[i] 大于等于情况一起处理了呢， 其实 等于的情况 也是当前的 容器 右侧，只不过跟底面等高，$h\ast w$ 计算结果为 0 。

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> st;
        int sum = 0;
        for(int i = 0; i < height.size(); i++) {
            while(!st.empty() && height[st.top()] <= height[i]) {
                int low  = st.top();
                st.pop();
                if(!st.empty()) {
                    int h = min(height[st.top()], height[i]) - height[low];
                    int w = i - st.top() - 1;
                    sum += h * w;
                }
            }
            st.push(i);
        }
        return sum;
    }
};