传输线的物理基础（九）：N 截面集总电路模型

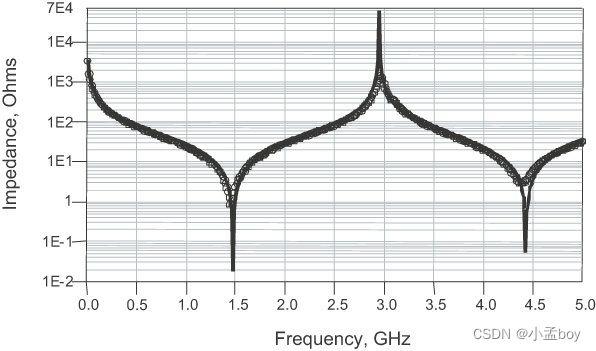
理想的传输线电路元件是一种分布式元件，可以非常准确地预测实际互连的测量性能。下图显示了 1 英寸长传输线在频域中的实测阻抗和仿真阻抗对比。我们看到甚至高达 5 GHz 的测量带宽也能达成出色的协议。

1英寸长、50欧姆传输线的测量（圆圈）和模拟（线路）阻抗。该模型是一条理想的无损传输线。在测量带宽范围内，一致性非常好。

 真实的互连将理想传输线模型的行为与高带宽相匹配。理想的输电线路模型对于实际的互连来说是一个非常好的模型。

我们可以用LC集总电路部分的组合来近似这个理想模型。我们如何知道在给定的精度水平下要使用多少LC切片？如果我们使用的部分太少会发生什么？这些问题可以使用SPICE这样的模拟工具来探讨。我们将首先在频域中工作，通过观察传输线的前端来评估阻抗，然后在时域中解释这一结果。
在频域中，我们可以问，在远端开路的情况下，观察传输线的前端时，阻抗是多少？在这个例子中，我们将使用一条50欧姆的线，它长6英寸，介电常数为4。它的时延为1纳秒。

总电容由 C = TD/Z = 1 纳秒/50 欧姆 = 20 pF 给出。总环路电感由 L = Z × TD = 50 Ohms × 1 nsec = 50 nH 给出。传输线最简单的近似是单个 LC 模型，其中 L 和 C 值作为传输线的总值。这是理想传输线的最简单的集总电路模型。
下图显示了理想分布式传输线的预测阻抗和使用这些值计算的单节 LC 集总电路模型的阻抗。在低频范围内，LC 模型的性能非常匹配。该模型的带宽约为 100 MHz。带宽的限制是因为，事实上，这条理想的传输线并没有在一个地方有它的所有电容。相反，它沿着长度分布，并且在每个电容器之间是一些与各部分的长度相关的环路电感。然而，从这个比较中可以清楚地看出，在远端开路的传输线在低频时看起来就像一个理想电容器。

理想传输线的仿真阻抗（圆圈）和单节 LC 集总电路模型（线）的仿真阻抗。该协议在高达约 100 MHz 的带宽范围内表现出色。

 理想传输线的阻抗显示了当频率与可以适合传输线长度的另一半波长匹配时出现的谐振峰。峰值谐振频率 f 由下式给出：

其中：
f = 阻抗峰值的频率
m = 峰值数，也就是适合传输线的半波数
TD = 传输线的时间延迟
f = 一个完整波适合传输线的频率
m = 1 的第一个谐振是 1 × 1 GHz/2 = 0.5 GHz。在这里，只有一个半波将均匀地适合传输线的长度，TD 为 1 纳秒。 m = 2 的第二个谐振位于 2 × 1 GHz/2 = 1 GHz。在这里，只有一个波适合传输线。这些驻波模式如下图所示。

传输线上的电压波。当额外的半波长可以适合线路时，就会发生共振。

 单节 LC 模型的带宽约为第一谐振频率的四分之一，最高可达约 125 MHz。我们可以通过将传输线分成更多部分来提高模型的带宽。如果我们将其分成两部分，则每个部分都可以建模为相同的 LC 模型，并且每个 L 和 C 的值将为 L /2 和 C /2。与理想 T 线相比，此两段 LC 模型的预测阻抗如图 7-40 所示。该模型的带宽大致为第一个共振峰的一半。这是大约 250 MHz 的频率。

理想传输线的仿真阻抗（圆圈）和一段和两段 LC 集总电路模型（线）的仿真阻抗。

 我们可以通过将长度分成更多的 LC 部分来进一步增加此集总电路模型的带宽。图 7-41 显示了与理想传输线的比较，使用 16 个不同的 LC 部分，每个 L 和 C 分别为 L /16 和 C /16。随着我们增加部分的数量，我们能够更好地近似于更高带宽的理想传输线的阻抗行为。该模型的带宽大约达到第四个共振峰，频率为 2 GHz。

理想传输线的仿真阻抗（圆圈）和 16 节 LC 集总电路模型（线）的仿真阻抗。

 n 节 LC 电路是理想传输线的近似值。部分越多，近似的带宽就越高。

我们可以根据这条理想传输线的时间延迟来估算 n 节集总电路模型的带宽。最后这些示例说明 LC 模型中的段越多，带宽越高。一个部分的带宽高达第一个谐振峰的四分之一； 2 个部分，最多为第一个共振的一半；和 16 个部分，直到第二个谐振频率。我们可以归纳出我们具有良好一致性的最高频率——模型的带宽——是：

或者：

 

其中：
BW=n段集总电路模型的带宽
n=模型中LC截面的数量
TD=传输线的时间延迟
f=一个完整波长的谐振频率=1/TD
通过使用n=10×BW×TD而不是n=8×BW×TD，我们将该关系近似为更保守且更易于记忆。

这是一个非常重要的经验法则，需要牢记在心。它说要达到等于 1/TD 的模型带宽，需要 10 个 LC 部分。它还表示，因为该频率对应于传输线中的一个波长，为了获得良好的近似值，信号的每 1/10 波长应该有一个 LC 部分。

例如，如果互连的 TD = 1 纳秒，而我们想要一个带宽为 5 GHz 的 n 节 LC 模型，那么我们至少需要 n = 10 × 5 GHz × 1 纳秒 = 50 个节。在这个最高频率下，传输线上将有 5 GHz × 1 纳秒 = 5 个波长。对于每一波，我们需要 10 个部分；因此，我们需要 5 × 10 = 50 个 LC 部分以获得良好的近似值。
如果一条线路的 TD 为 0.5 纳秒，而我们需要 2 GHz 的带宽，则所需的段数为 n = 10 × 2 GHz × 0.5 纳秒 = 10 段。
我们还可以评估我们可以使用单个 LC 部分来模拟传输线的频率。换句话说，传输线在什么频率下看起来像一个简单的 LC 电路？一段带宽为：

对于 TD = 1 纳秒的传输线，该线路的单节 LC 模型的带宽为 0.1 × 1/1 纳秒 = 100 MHz。如果 TD = 0.16 纳秒（大约 1 英寸长），则该线路的简单 LC 模型的带宽为 0.1 × 1/0.16 纳秒 = 600 MHz。传输线的时间延迟越长，我们可以将其近似为简单 LC 模型的频率就越低。

在评估我们需要描述所需带宽的传输线的部分数量时，我们发现信号的最高频率分量的每个波长需要大约 10 个 LC 部分，并且 LC 部分的总数取决于数量可以适合传输线的信号的最高频率分量的波长。 

如果我们有一个上升时间为RT的信号，则与该信号相关的带宽（重要的最高正弦波频率分量）为BW=0.35/RT。如果我们有时间延迟为TD的传输线，并且我们希望用n段集总电路模型来近似它，则我们需要确保模型的带宽BW至少大于BW：

 

 

其中：

 BW sig= 信号带宽
BW model= 模型的带宽
RT = 信号的上升时间
TD = 传输线的时间延迟
n = 精确模型所需的最小 LC 部分数

例如，上升时间为 0.5 纳秒，时间延迟为 1 纳秒，我们需要 n > 3.5 × 1/0.5 = 7 个部分才能获得准确的模型。当上升时间等于我们要建模的线路的 TD 时，我们至少需要 3.5 个部分才能获得准确的模型。在这种情况下，上升时间的空间范围就是传输线的长度。这暗示了一个非常重要的经验法则，在以下提示中给出。

为了将互连准确地描述为n截面LC模型，我们需要沿着前缘的空间范围具有至少3.5个LC截面。就好像信号的前沿的每三分之一与互连大致作为集总电路元件相互作用一样。

这个经验法则如下图所示。在 FR4 中，如果上升时间为 1 纳秒，则前沿的空间范围为 6 英寸。每 6 英寸长度需要 3.5 个 LC 部分，或每个部分约 1.7 英寸。我们可以这样概括：如果上升时间是 RT，信号的速度是 v，那么每个 LC 部分的长度是 (RT × v)/3.5。在 FR4 中，速度约为 6 英寸/纳秒，上升时间所需的每个 LC 部分的长度 RT 为 1.7 × RT，上升时间以纳秒为单位。

作为一般经验法则，每个上升时间的空间范围至少应有 3.5 个 LC 部分，以便在信号带宽处建立准确的互连模型。

 这是一个非常强大的经验法则：对于给定上升时间 RT（以纳秒为单位）的 n 部分集总电路模型的足够带宽，每个 LC 部分的尺寸（以英寸为单位）不应超过 1.7 × RT 英寸。

如果上升时间为 1 纳秒，则每个单个 LC 的长度应小于 1.7 英寸。如果上升时间为 0.5 纳秒，则每个 LC 部分的长度不应超过 0.5 × 1.7 = 0.85 英寸。

当然，理想的分布式传输线模型始终是低频和高频统一互连的良好模型。
本节中的分析评估了以足够的精度对高达信号带宽的真实传输进行建模所需的许多 LC 部分的最少数量。但这仍然是带宽有限的近似值。这就是为什么在为实际传输线选择模型时，首选应该始终是理想传输线，由特性阻抗和时间延迟定义。只有在非常罕见的情况下，当问题用 L 或 C 值来表述时，才应该使用 n 节集总模型来模拟真实的传输线。始终从理想的传输线模型开始。