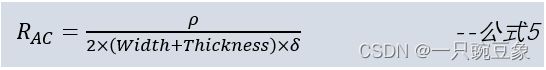传输线设计的参量解析

目录

序言

传输线分布参数模型

电感和电容的计算

高频损耗

导体直流电阻

导体交流电阻

介质损耗

分布电感、电容与介电常数的关系

参考文献

序言

        讨论传输线效应，就必须转变传统的电路分析思维，在电路分析中，不论是戴维南定理，还是基尔霍夫电压电流定律，其分析的基本出发点：在做等效计算时，电路任一时刻的电压电流可近似看为不发生任何波动，即实际传输线的长度远小于电路工作时的电磁波长，此时，电路模型可看成是集总参数模型，而在高速传输系统中，实际传输线的长度远大于工作时的电磁波长，在线路上的每一时刻，电压电流都在发生变化，此时，必须考虑电路分布性参数对变化信号的影响，电路模型就需要看成是分布参数模型。

传输线分布参数模型

        传输线必须用大量的R-L-C-G单元∆z表示，如下图所示，理想状态下，这样的单元数量是无限的，随着传输的信号频率越高，所用的单元越多，模型才能越准确，通用的规则是：工作在频域时，如果导线的长度大于波长的1/10，或者，工作在时域时，如果信号的上升时间小于两倍的传输时延，导线就应作为传输线进行分布参数计算（请记住这句话，在后续关于TDR的文章中，会运用这个规则）。

        如下图所示，R表示单位长度导线的电阻值，单位是Ω/m；L表示单位长度导线的电感值，单位是H/m；C表示单位长度导线间的电容值，单位是C/m；G表示隔开两导线的介质材料单位长度的电导（电阻的倒数）值，单位是S/m。

        利用这一分布参数模型，就可以求解出有损传输线的特性阻抗如公式1所示，公式的推导较为繁琐，大家可以参考微波工程类的书籍（如参考文献5），书里均有详细的求解过程，本文不再赘述。

        如果是无耗传输，则R=0和G=0，公式1可改写为公式2：

电感和电容的计算

        在小编看来，通常描述传输线性能的仅是特性阻抗和单位长度电容，利用这两个参数，即可以快速计算出单位长度的电感，因此，回归到工程应用上，常用的一种微带线的分布电容、电感及特性阻抗的快速计算公式集合如下：

        利用这个公式集合，以单端50Ω微带线为例，小编计算了不同规格下的导线分布参数，通过对计算结果的横向对比，可以获取如下信息：

        导线的分布电感≈ 0.28 nH/mm

        导线的分布电容≈ 0.1 pF/mm

        可以看出，相比于分布电容，单位长度走线的分布电感的量级更大，对高速传输系统造成的影响也会更为显著（这点在信号反射及串扰中需要着重关注和考察）。

 ​​

高频损耗

        以上讨论了L和C参量在传输线模型中的应用，但是，无耗传输线模型显然不适用于从1MHz往上的工作情况，因为它不能计算信号沿传输线传输时的高频损耗，传输线的损耗有两种基本类型：

        1. 源于导体电阻的欧姆损耗，影响有损传输线公式中的R参量；

        2. 源于介质材料的介质损耗，影响有损传输线公式中的G参量；

导体直流电阻

        欧姆损耗是唯一和导体性能相关的传输线参数，其它的参数均是介质材料或尺寸的函数，导线的电阻分为直流电阻和交流电阻，如下图所示，一个矩形横截面导体的直流电阻计算如公式3所示：

        如下表所示，计算了厚17um铜导线在不同尺寸下的直流欧姆损耗，通过数据对比，可以发现：

        1. 当导线是正方形结构时（即Length = Width），欧姆损耗值恒定为1mΩ，此可以作为经验值进行使用；

        2. 线宽固定的情况下，走线越长，造成的欧姆损耗越大，产生的直流电平压降越大；

        3. 线长固定的情况下，走线越宽，造成的欧姆损耗越小，产生的直流电平压降越小；

        以上结论可以对直流压降的评估起到很好的理论支撑作用。

导体交流电阻

        如下图所示，由于趋肤效应，高频工作时的信号电流只在导线的表面流过，并且，随着工作频率的增高，导线横截面上的电流越往导线的外表面集中，即常说的趋肤深度更大。

        常见的铜的趋肤深度如公式4所示，可见，随着频率值的增高，δ_copper 取值越小，表示趋肤效应越显著；

        而矩形横截面的交流阻抗计算与趋肤参数紧密相关，如公式5所示： 

        将式4代入式5可得到矩形铜导线的交流电阻表达式如公式6所示： 

        注意，以上所有的电阻方程均假设是单独一根直导线，实际的情况，可能会更为复杂，需要考虑导线间的互感和互容，这点已经超出了本文讨论的范畴，不再赘述。

        利用公式6，计算了厚17um铜导线工作在100MHz情况下，不同尺寸下的交流欧姆损耗，通过数据对比，可以发现，导线越长，导线宽度越小，带来的交流累积阻抗就越大，与导线单位电感同步进行考虑时，对于高频信号的衰减将更为明显，这也就是为何在高速链路系统设计中，需要对PCB走线提出长度及阻抗控制的要求；

介质损耗

        介质材料的损耗取决于材料的耗散因数，耗散因数定义为每赫兹材料的存储能量与耗散能量的比值，通常用损耗角正切tan⁡(δ)表示，材料的tan⁡(δ)越大，损耗越高，介质损耗的表达式如公式7所示：

        举例来说，当f_GHz=1， tan⁡(δ)=0.02， ϵ_r=4时， α_dielectric=0.092 dB/in，即1英寸产生0.092dB介质损耗，换句话说，如果是1V的信号幅度，最终幅度衰减后为0.989V。

        通常，如果按照前文的传输线尺寸判定原则，对于一个短传输线而言，介质损耗几乎可以被忽略，直到频率达到1GHz及以上时，才会加以考虑。

        关于耗散因数、损耗角正切，本文不做展开讨论，感兴趣的小伙伴，可以从参考文献[1]的9.5章节中，获取详细的描述。

分布电感、电容与介电常数的关系

        最后，讨论下这三者之间的联系，由于传播速度是介质材料的函数，而介质材料与传输线的电感和电容有关，因此，如公式8所示，电感、电容和速度其实都是相关的；

        --c是自由空间中光的速度=3×10^8 / 

        将特性阻抗的表达公式2带入公式8中，可以计算出传输线的L和C的表达式：

        这两个公式在实际工程应用中，将会非常有用，它们表明了传输线的特性阻抗、电容、电感和介电常数之间的关系，请谨记！

        针对本文如有任何的技术问题，欢迎大家在文章下方给与评论，或者私信，小编将在最快的时间内回复大家的问题！！！

参考文献

        [1] Signal Integrity: Simplified 1st Edition, Eric Bogatin

        [2] High-Speed Circuit Board Signal Integrity, 2nd Edition, Stephen C Thierauf

        [3] Printed Circuit Board Design Techniques for EMC Compliance: A Handbook for Designers, 2nd Edition, Mark I. Montrose

        [4] Electromagnetic Compatibility Engineering, Henry W.Ott

        [5] Microwave Engineering, 4th Edition, David M. Pozar