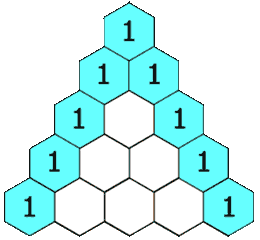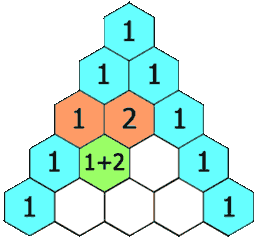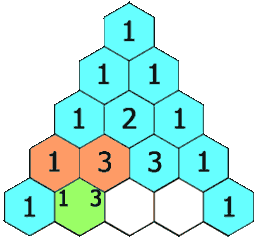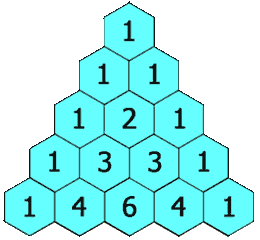
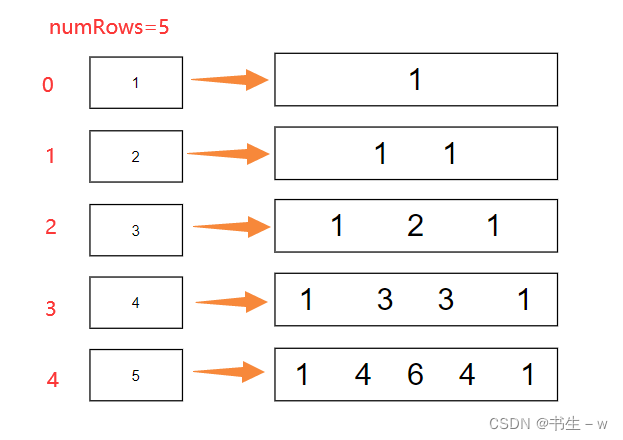
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- Long类型前后端数据不一致
igotyback
前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题,尤其是当后端使用Java的Long类型(64位)与前端JavaScript的Number类型(最大安全整数为2^53-1,即16位)进行数据交互时,很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
- LocalDateTime 转 String
igotyback
java开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
- Linux下QT开发的动态库界面弹出操作(SDL2)
13jjyao
QT类qt开发语言sdl2linux
需求:操作系统为linux,开发框架为qt,做成需带界面的qt动态库,调用方为java等非qt程序难点:调用方为java等非qt程序,也就是说调用方肯定不带QApplication::exec(),缺少了这个,QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出);这与qt调用本身qt库是有本质的区别的思路:1.调用方缺QApplication::exec(),那么我们在接口
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
- 【华为OD机试真题2023B卷 JAVA&JS】We Are A Team
若博豆
java算法华为javascript
华为OD2023(B卷)机试题库全覆盖,刷题指南点这里WeAreATeam时间限制:1秒|内存限制:32768K|语言限制:不限题目描述:总共有n个人在机房,每个人有一个标号(1<=标号<=n),他们分成了多个团队,需要你根据收到的m条消息判定指定的两个人是否在一个团队中,具体的:1、消息构成为:abc,整数a、b分别代
- 数组去重
好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考?如何去除数组中重复的项例如数组:[1,3,4,3,5]我们在做去重的时候,一开始想到的肯定是,逐个比较,外面一层循环,内层后一个与前一个一比较,如果是久不将当前这一项放进新的数组,挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低,代码量还多,思考?有没有更好的方法这时候不禁一想当然有了!!!hashtable啊,通过对象的hash办法
- 关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript
二挡起步
web前端期末大作业javascripthtmlcss旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业,Web大学生网页HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
- HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
- 回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
- Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
- Faiss:高效相似性搜索与聚类的利器
网络·魚
大数据faiss
Faiss是一个针对大规模向量集合的相似性搜索库,由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构,用于加速向量之间的相似性搜索,特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理:近似最近邻搜索:Faiss的核心功能之一是近似最近邻搜索,它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的,
- 数据结构之哈希表
X同学的开始
数据结构数据结构散列表
哈希表(散列表)出现的原因在顺序表中查找时,需要从表头开始,依次遍历比较a[i]与key的值是否相等,直到相等才返回索引i;在有序表中查找时,我们经常使用的是二分查找,通过比较key与a[i]的大小来折半查找,直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是,这两种方法的效率都依赖于查找中比较的次数。我们有一种想法,能不能不经过比较,而是直接通过关键字key一次得到所要的结果呢?这时,
- insert into select 主键自增_mybatis拦截器实现主键自动生成
weixin_39521651
insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
前言前阵子和朋友聊天,他说他们项目有个需求,要实现主键自动生成,不想每次新增的时候,都手动设置主键。于是我就问他,那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成,因此为了项目稳定性,不会切换id的生成方式。朋友问我有没有什么实现思路,他们公司的orm框架是mybatis,我就建议他说,不然让你老大把mybatis切换成mybatis-plus。mybat
- k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题)
寻找你83497
k均值聚类算法考试例题
?算法:第一步:选K个初始聚类中心,z1(1),z2(1),…,zK(1),其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定,例如可选开始的K个.k均值聚类:---------一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则;模糊的c均值聚类算法:--------一种模糊聚类算法,是.K均值聚类算法是先随机选取K个对象作为初始的聚类
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- Java 重写(Override)与重载(Overload)
叨唧唧的
Java重写(Override)与重载(Overload)重写(Override)重写是子类对父类的允许访问的方法的实现过程进行重新编写,返回值和形参都不能改变。即外壳不变,核心重写!重写的好处在于子类可以根据需要,定义特定于自己的行为。也就是说子类能够根据需要实现父类的方法。重写方法不能抛出新的检查异常或者比被重写方法申明更加宽泛的异常。例如:父类的一个方法申明了一个检查异常IOExceptio
- 简单了解 JVM
记得开心一点啊
jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称,意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统(如:JVM、VMwave、VirtualBox)。JVM和其他两个虚拟机
- 1分钟解决 -bash: mvn: command not found,在Centos 7中安装Maven
Energet!c
开发语言
1分钟解决-bash:mvn:commandnotfound,在Centos7中安装Maven检查Java环境1下载Maven2解压Maven3配置环境变量4验证安装5常见问题与注意事项6总结检查Java环境Maven依赖Java环境,请确保系统已经安装了Java并配置了环境变量。可以通过以下命令检查:java-version如果未安装,请先安装Java。1下载Maven从官网下载:前往Apach
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- Java企业面试题3
马龙强_
java
1.break和continue的作用(智*图)break:用于完全退出一个循环(如for,while)或一个switch语句。当在循环体内遇到break语句时,程序会立即跳出当前循环体,继续执行循环之后的代码。continue:用于跳过当前循环体中剩余的部分,并开始下一次循环。如果是在for循环中使用continue,则会直接进行条件判断以决定是否执行下一轮循环。2.if分支语句和switch分
- JVM、JRE和 JDK:理解Java开发的三大核心组件
Y雨何时停T
Javajava
Java是一门跨平台的编程语言,它的成功离不开背后强大的运行环境与开发工具的支持。在Java的生态中,JVM(Java虚拟机)、JRE(Java运行时环境)和JDK(Java开发工具包)是三个至关重要的核心组件。本文将探讨JVM、JDK和JRE的区别,帮助你更好地理解Java的运行机制。1.JVM:Java虚拟机(JavaVirtualMachine)什么是JVM?JVM,即Java虚拟机,是Ja
- 推荐算法_隐语义-梯度下降
_feivirus_
算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵,值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
- K近邻算法_分类鸢尾花数据集
_feivirus_
算法机器学习和数学分类机器学习K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
- Java面试题精选:消息队列(二)
芒果不是芒
Java面试题精选javakafka
一、Kafka的特性1.消息持久化:消息存储在磁盘,所以消息不会丢失2.高吞吐量:可以轻松实现单机百万级别的并发3.扩展性:扩展性强,还是动态扩展4.多客户端支持:支持多种语言(Java、C、C++、GO、)5.KafkaStreams(一个天生的流处理):在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制:Kafka进行生产或者消费的时候会
- jQuery 跨域访问的三种方式 No 'Access-Control-Allow-Origin' header is present on the reque
qiaolevip
每天进步一点点学习永无止境跨域众观千象
XMLHttpRequest cannot load http://v.xxx.com. No 'Access-Control-Allow-Origin' header is present on the requested resource. Origin 'http://localhost:63342' is therefore not allowed access. test.html:1
- mysql 分区查询优化
annan211
java分区优化mysql
分区查询优化
引入分区可以给查询带来一定的优势,但同时也会引入一些bug.
分区最大的优点就是优化器可以根据分区函数来过滤掉一些分区,通过分区过滤可以让查询扫描更少的数据。
所以,对于访问分区表来说,很重要的一点是要在where 条件中带入分区,让优化器过滤掉无需访问的分区。
可以通过查看explain执行计划,是否携带 partitions
- MYSQL存储过程中使用游标
chicony
Mysql存储过程
DELIMITER $$
DROP PROCEDURE IF EXISTS getUserInfo $$
CREATE PROCEDURE getUserInfo(in date_day datetime)-- -- 实例-- 存储过程名为:getUserInfo-- 参数为:date_day日期格式:2008-03-08-- BEGINdecla
- mysql 和 sqlite 区别
Array_06
sqlite
转载:
http://www.cnblogs.com/ygm900/p/3460663.html
mysql 和 sqlite 区别
SQLITE是单机数据库。功能简约,小型化,追求最大磁盘效率
MYSQL是完善的服务器数据库。功能全面,综合化,追求最大并发效率
MYSQL、Sybase、Oracle等这些都是试用于服务器数据量大功能多需要安装,例如网站访问量比较大的。而sq
- pinyin4j使用
oloz
pinyin4j
首先需要pinyin4j的jar包支持;jar包已上传至附件内
方法一:把汉字转换为拼音;例如:编程转换后则为biancheng
/**
* 将汉字转换为全拼
* @param src 你的需要转换的汉字
* @param isUPPERCASE 是否转换为大写的拼音; true:转换为大写;fal
- 微博发送私信
随意而生
微博
在前面文章中说了如和获取登陆时候所需要的cookie,现在只要拿到最后登陆所需要的cookie,然后抓包分析一下微博私信发送界面
http://weibo.com/message/history?uid=****&name=****
可以发现其发送提交的Post请求和其中的数据,
让后用程序模拟发送POST请求中的数据,带着cookie发送到私信的接入口,就可以实现发私信的功能了。
- jsp
香水浓
jsp
JSP初始化
容器载入JSP文件后,它会在为请求提供任何服务前调用jspInit()方法。如果您需要执行自定义的JSP初始化任务,复写jspInit()方法就行了
JSP执行
这一阶段描述了JSP生命周期中一切与请求相关的交互行为,直到被销毁。
当JSP网页完成初始化后
- 在 Windows 上安装 SVN Subversion 服务端
AdyZhang
SVN
在 Windows 上安装 SVN Subversion 服务端2009-09-16高宏伟哈尔滨市道里区通达街291号
最佳阅读效果请访问原地址:http://blog.donews.com/dukejoe/archive/2009/09/16/1560917.aspx
现在的Subversion已经足够稳定,而且已经进入了它的黄金时段。我们看到大量的项目都在使
- android开发中如何使用 alertDialog从listView中删除数据?
aijuans
android
我现在使用listView展示了很多的配置信息,我现在想在点击其中一条的时候填出 alertDialog,点击确认后就删除该条数据,( ArrayAdapter ,ArrayList,listView 全部删除),我知道在 下面的onItemLongClick 方法中 参数 arg2 是选中的序号,但是我不知道如何继续处理下去 1 2 3
- jdk-6u26-linux-x64.bin 安装
baalwolf
linux
1.上传安装文件(jdk-6u26-linux-x64.bin)
2.修改权限
[root@localhost ~]# ls -l /usr/local/jdk-6u26-linux-x64.bin
3.执行安装文件
[root@localhost ~]# cd /usr/local
[root@localhost local]# ./jdk-6u26-linux-x64.bin&nbs
- MongoDB经典面试题集锦
BigBird2012
mongodb
1.什么是NoSQL数据库?NoSQL和RDBMS有什么区别?在哪些情况下使用和不使用NoSQL数据库?
NoSQL是非关系型数据库,NoSQL = Not Only SQL。
关系型数据库采用的结构化的数据,NoSQL采用的是键值对的方式存储数据。
在处理非结构化/半结构化的大数据时;在水平方向上进行扩展时;随时应对动态增加的数据项时可以优先考虑使用NoSQL数据库。
在考虑数据库的成熟
- JavaScript异步编程Promise模式的6个特性
bijian1013
JavaScriptPromise
Promise是一个非常有价值的构造器,能够帮助你避免使用镶套匿名方法,而使用更具有可读性的方式组装异步代码。这里我们将介绍6个最简单的特性。
在我们开始正式介绍之前,我们想看看Javascript Promise的样子:
var p = new Promise(function(r
- [Zookeeper学习笔记之八]Zookeeper源代码分析之Zookeeper.ZKWatchManager
bit1129
zookeeper
ClientWatchManager接口
//接口的唯一方法materialize用于确定那些Watcher需要被通知
//确定Watcher需要三方面的因素1.事件状态 2.事件类型 3.znode的path
public interface ClientWatchManager {
/**
* Return a set of watchers that should
- 【Scala十五】Scala核心九:隐式转换之二
bit1129
scala
隐式转换存在的必要性,
在Java Swing中,按钮点击事件的处理,转换为Scala的的写法如下:
val button = new JButton
button.addActionListener(
new ActionListener {
def actionPerformed(event: ActionEvent) {
- Android JSON数据的解析与封装小Demo
ronin47
转自:http://www.open-open.com/lib/view/open1420529336406.html
package com.example.jsondemo;
import org.json.JSONArray;
import org.json.JSONException;
import org.json.JSONObject;
impor
- [设计]字体创意设计方法谈
brotherlamp
UIui自学ui视频ui教程ui资料
从古至今,文字在我们的生活中是必不可少的事物,我们不能想象没有文字的世界将会是怎样。在平面设计中,UI设计师在文字上所花的心思和功夫最多,因为文字能直观地表达UI设计师所的意念。在文字上的创造设计,直接反映出平面作品的主题。
如设计一幅戴尔笔记本电脑的广告海报,假设海报上没有出现“戴尔”两个文字,即使放上所有戴尔笔记本电脑的图片都不能让人们得知这些电脑是什么品牌。只要写上“戴尔笔
- 单调队列-用一个长度为k的窗在整数数列上移动,求窗里面所包含的数的最大值
bylijinnan
java算法面试题
import java.util.LinkedList;
/*
单调队列 滑动窗口
单调队列是这样的一个队列:队列里面的元素是有序的,是递增或者递减
题目:给定一个长度为N的整数数列a(i),i=0,1,...,N-1和窗长度k.
要求:f(i) = max{a(i-k+1),a(i-k+2),..., a(i)},i = 0,1,...,N-1
问题的另一种描述就
- struts2处理一个form多个submit
chiangfai
struts2
web应用中,为完成不同工作,一个jsp的form标签可能有多个submit。如下代码:
<s:form action="submit" method="post" namespace="/my">
<s:textfield name="msg" label="叙述:">
- shell查找上个月,陷阱及野路子
chenchao051
shell
date -d "-1 month" +%F
以上这段代码,假如在2012/10/31执行,结果并不会出现你预计的9月份,而是会出现八月份,原因是10月份有31天,9月份30天,所以-1 month在10月份看来要减去31天,所以直接到了8月31日这天,这不靠谱。
野路子解决:假设当天日期大于15号
- mysql导出数据中文乱码问题
daizj
mysql中文乱码导数据
解决mysql导入导出数据乱码问题方法:
1、进入mysql,通过如下命令查看数据库编码方式:
mysql> show variables like 'character_set_%';
+--------------------------+----------------------------------------+
| Variable_name&nbs
- SAE部署Smarty出现:Uncaught exception 'SmartyException' with message 'unable to write
dcj3sjt126com
PHPsmartysae
对于SAE出现的问题:Uncaught exception 'SmartyException' with message 'unable to write file...。
官方给出了详细的FAQ:http://sae.sina.com.cn/?m=faqs&catId=11#show_213
解决方案为:
01
$path
- 《教父》系列台词
dcj3sjt126com
Your love is also your weak point.
你的所爱同时也是你的弱点。
If anything in this life is certain, if history has taught us anything, it is
that you can kill anyone.
不顾家的人永远不可能成为一个真正的男人。 &
- mongodb安装与使用
dyy_gusi
mongo
一.MongoDB安装和启动,widndows和linux基本相同
1.下载数据库,
linux:mongodb-linux-x86_64-ubuntu1404-3.0.3.tgz
2.解压文件,并且放置到合适的位置
tar -vxf mongodb-linux-x86_64-ubun
- Git排除目录
geeksun
git
在Git的版本控制中,可能有些文件是不需要加入控制的,那我们在提交代码时就需要忽略这些文件,下面讲讲应该怎么给Git配置一些忽略规则。
有三种方法可以忽略掉这些文件,这三种方法都能达到目的,只不过适用情景不一样。
1. 针对单一工程排除文件
这种方式会让这个工程的所有修改者在克隆代码的同时,也能克隆到过滤规则,而不用自己再写一份,这就能保证所有修改者应用的都是同一
- Ubuntu 创建开机自启动脚本的方法
hongtoushizi
ubuntu
转载自: http://rongjih.blog.163.com/blog/static/33574461201111504843245/
Ubuntu 创建开机自启动脚本的步骤如下:
1) 将你的启动脚本复制到 /etc/init.d目录下 以下假设你的脚本文件名为 test。
2) 设置脚本文件的权限 $ sudo chmod 755
- 第八章 流量复制/AB测试/协程
jinnianshilongnian
nginxluacoroutine
流量复制
在实际开发中经常涉及到项目的升级,而该升级不能简单的上线就完事了,需要验证该升级是否兼容老的上线,因此可能需要并行运行两个项目一段时间进行数据比对和校验,待没问题后再进行上线。这其实就需要进行流量复制,把流量复制到其他服务器上,一种方式是使用如tcpcopy引流;另外我们还可以使用nginx的HttpLuaModule模块中的ngx.location.capture_multi进行并发
- 电商系统商品表设计
lkl
DROP TABLE IF EXISTS `category`; -- 类目表
/*!40101 SET @saved_cs_client = @@character_set_client */;
/*!40101 SET character_set_client = utf8 */;
CREATE TABLE `category` (
`id` int(11) NOT NUL
- 修改phpMyAdmin导入SQL文件的大小限制
pda158
sqlmysql
用phpMyAdmin导入mysql数据库时,我的10M的
数据库不能导入,提示mysql数据库最大只能导入2M。
phpMyAdmin数据库导入出错: You probably tried to upload too large file. Please refer to documentation for ways to workaround this limit.
- Tomcat性能调优方案
Sobfist
apachejvmtomcat应用服务器
一、操作系统调优
对于操作系统优化来说,是尽可能的增大可使用的内存容量、提高CPU的频率,保证文件系统的读写速率等。经过压力测试验证,在并发连接很多的情况下,CPU的处理能力越强,系统运行速度越快。。
【适用场景】 任何项目。
二、Java虚拟机调优
应该选择SUN的JVM,在满足项目需要的前提下,尽量选用版本较高的JVM,一般来说高版本产品在速度和效率上比低版本会有改进。
J
- SQLServer学习笔记
vipbooks
数据结构xml
1、create database school 创建数据库school
2、drop database school 删除数据库school
3、use school 连接到school数据库,使其成为当前数据库
4、create table class(classID int primary key identity not null)
创建一个名为class的表,其有一
![]()
![]()