第五十九章 线段树（二）

一、懒标记（lazy_tag）

1、作用

通过第五十八章节的讲解，我们发现在上一章节中实现的线段树操作只能实现单点修改。如果是题目中要求的是区间修改操作，我们可以对该区间中的每个点进行单点修改，该思路的时间复杂度是$O(nlogn)$的，但是如果我们想要通过$O(logn)$的时间复杂度去实现区间修改的话，就必须使用今天所讲解的懒标记。

2、思路

懒标记的思路源于我们的查询操作。我们先回顾一下线段树的区间查询操作，查询函数的复杂度是$O(logn)$的，他的思想就是用尽量少的子区间拼出当前区间。
如下图所示：

我们就可以借用这个思路去实现区间修改，假设我们现在想给红色区间内的每一个数字都加上一个数，那么我们只需要找到拼出该红色区间的蓝色区间，给每个蓝色区间都打上一个标记。这个标记的含义是：给当前区间的所有子区间都加上一个数 （不包含当前区间）。

二、结构体定义

struct Node
{
	int l, r;
	int sum;
	int tag;//懒标记
}tre[N * 4];

三、带有懒标记的函数操作

我们现在就以给整个区间加上一个数字为例。

1、pushup函数

这个函数我们很熟悉了，这个函数的作用就是利用子节点去更新当前节点的和。

void pushup(int u)
{
	tre[u].sum = tre[u << 1].sum + tre[u << 1 | 1].sum;
}

2、build函数

这个函数的作用就是去利用最初的原始数据建立其我们的线段树。递归建好线段树以后，我们还需要利用子区间的和维护出当前区间的信息，即在最后加上一个$pushup$操作。同时，由于我们一开始并没有给任何区间加上数字，所以我们的懒标记初始化为0即可。

void build(int u, int l, int r)
{
	if(l == r)
		tre[u] = {l, r, a[l], 0};
	else
	{
		tre[u] = {l, r};
		int mid = tre[u].l + tre[u].r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

3、modify函数

这个函数的作用就是给一个区间加上一个数字。那么如何实现呢？我们看下面的图：

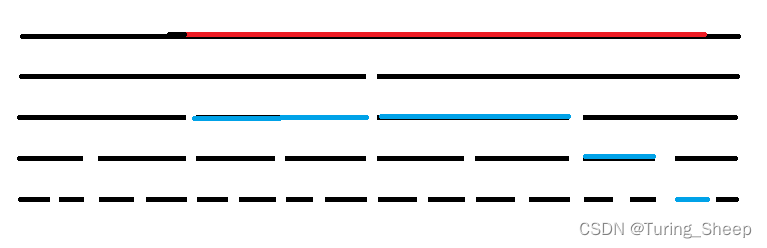
这个红色覆盖的区间可以分为两类。一类是完全被覆盖的区间，比如蓝色区间，那么对于这些蓝色区间而言直接加上一个懒标记即可。但是由于我们的懒标记的定义是给当前节点的子节点都加上一个数，并不包括当前节点，所以对于当前节点所维护的区间和而言，我们需要手动添加。

另外一类区间即只有部分被红色区间覆盖。那么这些区间应该怎么办呢？

由于我们的懒标记是针对整个区间而言的，所以这些部分被覆盖的区间是不能去加懒标记的。我们只能把部分覆盖转化为完全覆盖。即将当前父节点的懒标记传递给子节点，并且清空当前父节点的懒标记。直到懒标记所在的区间被红色区间完全覆盖。而这个懒标记下放的操作叫做$pushdown$。

$pushdown$函数具体怎么实现我们放到后面讲。当我们修改以后，我们还需要利用$pushup$操作更新当前节点的数值。

void modify(int u, int l, int r, int d)
{
	if(tre[u].l >= l && tre[u].r <= r)
	{
		tre[u].sum += (tre[u].r - tre[u].l + 1) * d;
		tre[u].tag += d;
	}
	else
	{
		pushdown(u);//懒标记下放
		int mid = tre[u].l + tre[u].r >> 1;
		if(l <= mid)
			modify(u << 1, l, r, d);
		if(r > mid)
			modify(u << 1 | 1, l, r, d);
		pushup(u);
	}
}

4、pushdown函数

我们再回顾一下懒标记的作用：给当前区间的子区间都加上一个数（不包括当前区间）。

同时，根据我们刚刚的$modify$函数可知，我们的$pushdown$函数的作用是将当前区间的懒标记传递给子节点。并且清空父节点的懒标记。为什么需要清空呢？因为如果不清空的话，对于当前区间的儿子的儿子而言，由于其父亲和父亲的父亲都有懒标记，所以这个区间会被重复加上一个数字，因此我们需要清空。

现在，我们需要根据刚刚的懒标记的作用来实现$pushdown$函数。
我们将标记下传的同时，需要给左右子节点维护的区间和都加上父节点的懒标记所记录的数值。同时，还需给左右子节点维护的懒标记加上该数值。左右子节点的懒标记加上该数值很好理解，但是为什么左右子节点的区间和也要加上这个数值呢？

因为我们的懒标记是说给子树加上一个数值，而不是当前区间，也就是说如果我们只把懒标记向下传递的话，我们的左右子节点所代表的区间和是不会加上该数值的。所以，我们需要进行该操作。

void pushdown(int u)
{
	auto &root = tre[u], &left = tre[u << 1], &right = tre[u << 1 | 1];
	if(root.tag)
	{
		left.sum += (left.r - left.l + 1) * root.tag;
		left.tag += root.tag;
		right.sum += (right.r - right.l + 1) * root.tag;
		right.tag += root.tag;
		root.tag = 0;
	}
}

5、query函数

query函数的作用是查询某个区间的区间和。我们$query$函数的思想是用尽可能少的区间去拼凑出当前查询的区间。那么在查询的过程中，如果某个区间只是部分被覆盖了，按照我们的逻辑，我们需要通过判断去递归查询该区间的子区间，但是此时我们就会面对一个问题。

这个问题就是：我们的懒标记只会给父节点标记，子节点上是没有标记的，假设我们讨论的这个部分覆盖的区间上是有懒标记的，我们查询到他的子区间的时候，子区间是没有标记的，但实际上这个区间是应该被加上一个数字的。

因此，为了解决这个问题，我们只需要在向下查询的时候，加上我们的$pushdown$操作。

int query(int u, int l, int r)
{
	if(tre[u].l >= l && tre[u].r <= r)
		return tre[u].sum;
	
	pushdown(u);
	int res = 0;
	int mid = tre[u].l + tre[u].r >> 1;
	if(l <= mid)
		res += query(u << 1, l, r);
	if(r > mid)
		res += query(u << 1 | 1, l, r);
	return res;
}

四、代码

#include
#define endl '\n'
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
int n, m;
int a[N];
struct Node
{
	int l, r;
	int sum;
	int tag;
}tre[N * 4];

void pushup(int u)
{
	tre[u].sum = tre[u << 1].sum + tre[u << 1 | 1].sum;
}

void pushdown(int u)
{
	auto &root = tre[u], &left = tre[u << 1], &right = tre[u << 1 | 1];
	if(root.tag)
	{
		left.sum += (left.r - left.l + 1) * root.tag;
		left.tag += root.tag;
		right.sum += (right.r - right.l + 1) * root.tag;
		right.tag += root.tag;
		root.tag = 0;
	}
}

void build(int u, int l, int r)
{
	if(l == r)
		tre[u] = {l, r, a[l], 0};
	else
	{
		tre[u] = {l, r};
		int mid = tre[u].l + tre[u].r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

void modify(int u, int l, int r, int d)
{
	if(tre[u].l >= l && tre[u].r <= r)
	{
		tre[u].sum += (tre[u].r - tre[u].l + 1) * d;
		tre[u].tag += d;
	}
	else
	{
		pushdown(u);
		int mid = tre[u].l + tre[u].r >> 1;
		if(l <= mid)
			modify(u << 1, l, r, d);
		if(r > mid)
			modify(u << 1 | 1, l, r, d);
		pushup(u);
	}
}

int query(int u, int l, int r)
{
	if(tre[u].l >= l && tre[u].r <= r)
		return tre[u].sum;
	
	pushdown(u);
	int res = 0;
	int mid = tre[u].l + tre[u].r >> 1;
	if(l <= mid)
		res += query(u << 1, l, r);
	if(r > mid)
		res += query(u << 1 | 1, l, r);
	return res;
}

void solve()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ )
		cin >> a[i];
	build(1, 1, n);
	while(m--)
	{
		char opt;
		int l, r, d;
		cin >> opt >> l >> r;
		if(opt == 'C')
		{
			cin >> d;
			modify(1, l, r, d);
		}
		else
			cout << query(1, l, r) << endl;
	}
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	solve();
}