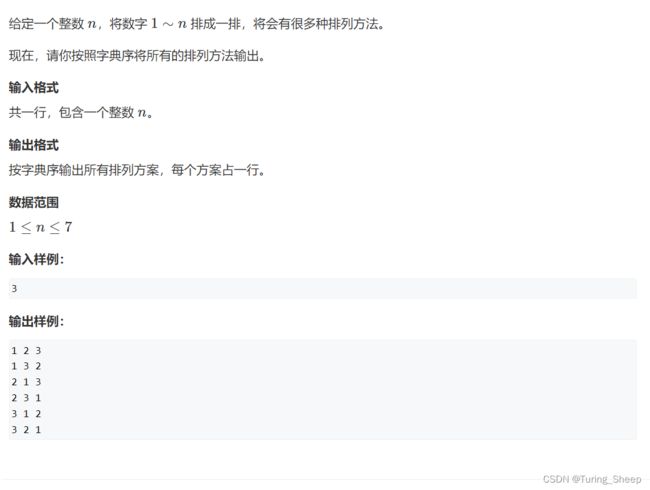
第十三章 DFS与BFS（保姆级教学！！超级详细的图示！！）

一、深度优先搜索

1、什么是DFS？

DFS即Depth First Search，深度优先搜索。简单地理解为一条路走到黑。那么什么叫一条路走到黑呢？假设我们想在如下的地图中走出一条最长的路，那么最粗暴的方式就是枚举出每一种情况。

因此，按照DFS一条路走到黑的思想，我们将会出现如下路线：

先走A，然后到B，到了B有三种情况，意味着这条路还没走完，那我就接着走，从B走到E，走到E之后没路了。那我就回溯到B,为什么呢？
因为我原本走到B的时候就有三种情况，但是刚刚只走了一种情况，因此我要回到B再去尝试第二条路，于是我们就从E回到B，然后从B去F。到了F，又没路了，那我们就回到B走第三种情况，从B到G。这样我们就走完了从A->B的三种情况。又因为在A处其实还有三种情况，因此我们走完B的三种情况后，回到A,去走除了从A->B的第二种情况，即A->C。由此以往。

简而言之，就是我们一头扎进去，撞了南墙，我就退一步，但是决不放弃，在原基础上做出局部的改变去尝试第二条路，直到所有的情况我都试了，实在没有其他情况了，那我就回到A，从头出发，再做选择，再一头扎进去，直到成功。

2、DFS代码模板

（1）问题：

（2）分析：

我们将其各种选择，继续画成一棵树：

这张图就清晰很多了，因此想要用DFS，我们首先要有逻辑地画出一张地图，有了地图才能去搜。

（3）模板：

#include
using namespace std;
const int N=10;
int ans[N];
bool mark[N];
int n;
void dfs(int u)
{
    //"回头"的条件
    if(u==n)
    {
        for(int i=0;i<n;i++)cout<<ans[i]<<" ";
        puts("");
        return;
    }
    
    for(int i=1;i<=n;i++)
    {
        if(mark[i]==false)
        {
            mark[i]=true;
            ans[u]=i;
            dfs(u+1);
            //复原
            mark[i]=false;
            ans[u]=0;
        }
    }
}

int main()
{
    cin>>n;
    dfs(0);
    return 0;
}

3、DFS代码分析

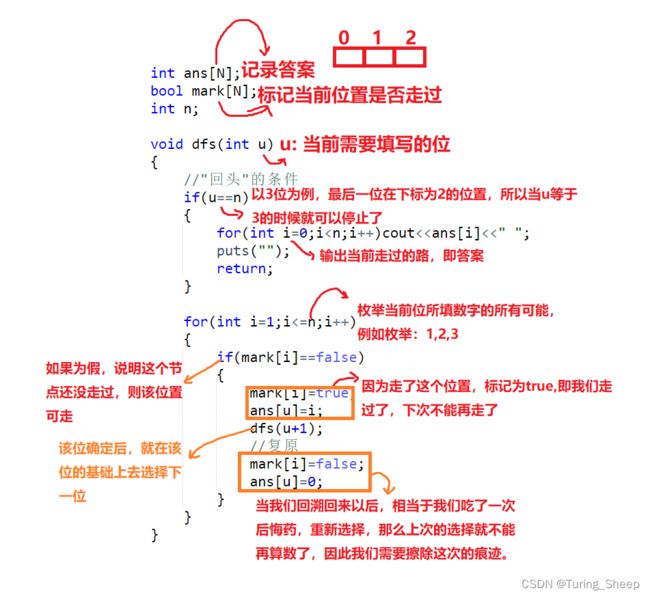
当然这个过程很抽象，那么我就帮大家模拟一下函数进行的过程吧^ _ ^（这里只模拟一部分，不理解的读者可自己模拟完。）

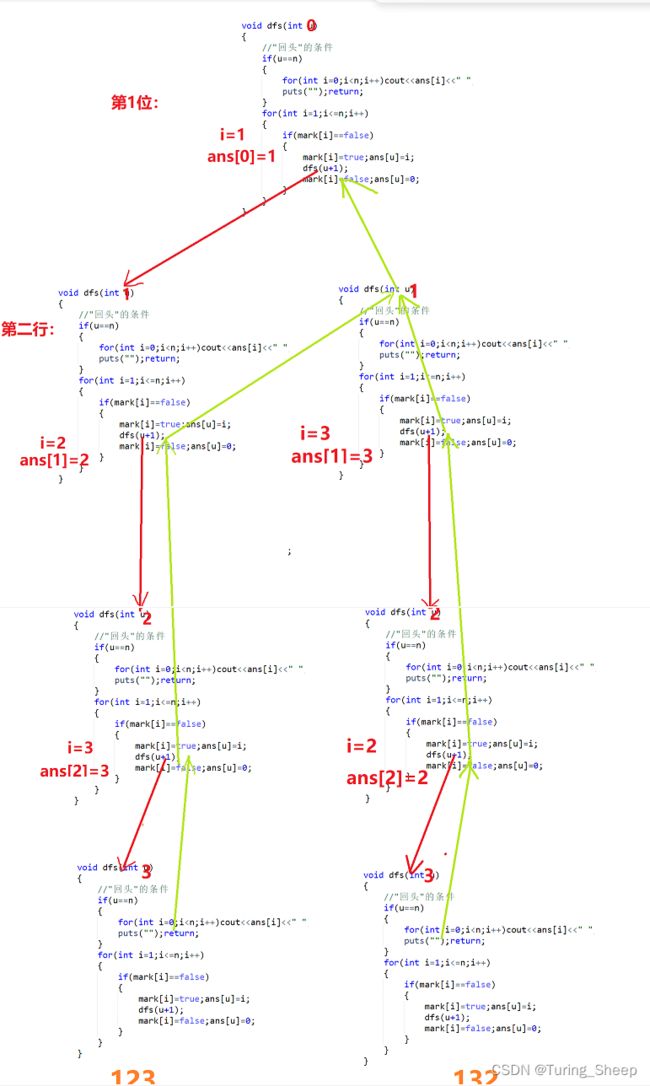
二、广度优先搜索

1、什么是BFS？

BFS即Breadth First Search，即广度优先搜索。如果说DFS是一条路走到黑的话，BFS就完全相反了。BFS会在每个岔路口都各向前走一步。因此其遍历顺序如下图所示：

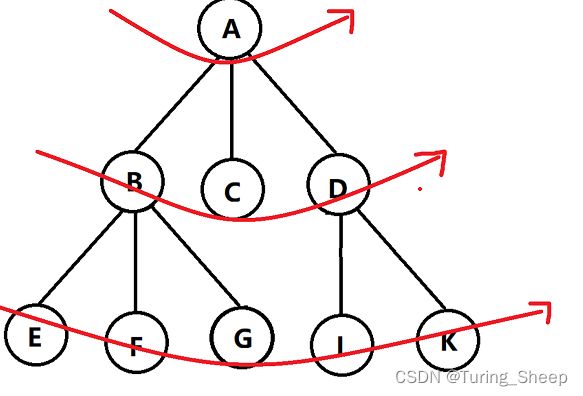
我们发现每次搜索的位置都是距离当前节点最近的点。因此，BFS是具有最短路的性质的。为什么呢？这就类似于我们后面要学习的贪心策略。这里简单地介绍一下贪心，假设我们可以做出12次选择。我们想得到一个最好的方案。那么我们可以在第一次选择的时候，做出当前最好的选择，在第二次选择的时候，再做出那时候最好的选择，由此积累。当我们在每次的选择面前，都做到了当前最好的选择，那么我们就可以由局部最优推出整体最优。

这里也是类似的，我们可以在每次出发的时候，走到离自己最近的点，由此我们每次都保证走最近的，那从局部最近推整体最近，必有一条路是整体最近的。所以我们可以利用BFS做最短路问题。

2、BFS代码模板

（1）问题：

本题求的是最短路，因此我们可以利用BFS从当前节点出发，每次都向周围拓展。

（2）代码：

#include
#include
#include
using namespace std;
const int N=110;
typedef pair<int,int> PII;
int map[N][N],mark[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1},n,m,ans;
void bfs()
{
    memset(mark,-1,sizeof mark);
    queue<PII>q;
    q.push({0,0});
    mark[0][0]=0;
    while(!q.empty())
    {
        PII top=q.front();
        for(int i=0;i<4;i++)
        {
            int nex=top.first+dx[i],ney=top.second+dy[i];
            if(nex>=0&&nex<n&&ney>=0&&ney<m&&mark[nex][ney]==-1&&map[nex][ney]==0)
            {
                mark[nex][ney]=mark[top.first][top.second]+1;
                q.push({nex,ney});
            }
        }
        q.pop();
    }
    cout<<mark[n-1][m-1];
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            scanf("%d",&map[i][j]);
        }
    }
    bfs();
}

3、BFS代码分析

（1）问题1：为什么要用队列？

BFS要保证的第一件事就是我们需要先走最近的，因此，队列的作用就是基于此的。

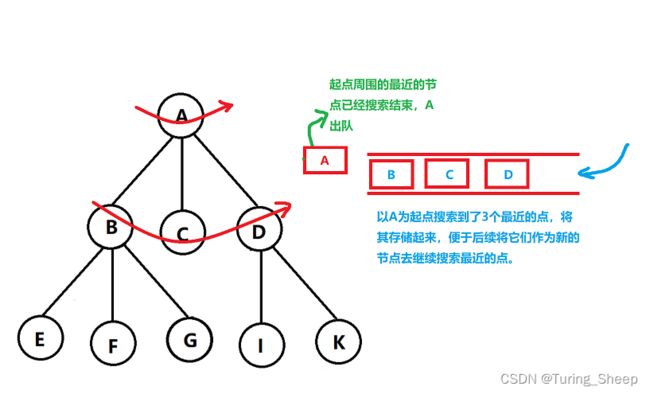
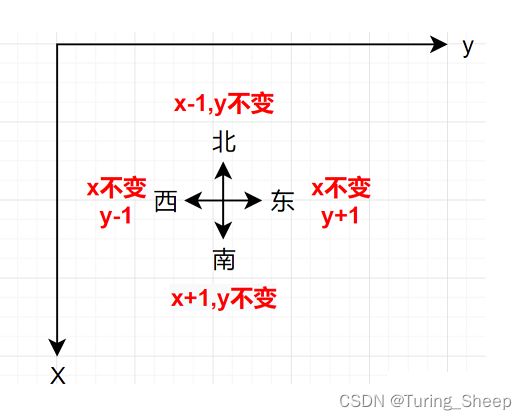
（2）问题2：方向向量怎么用？

我们将上面的方向变化可以写成如下的数组：

（3）问题3：为什么最后的输出是最短路？

我们每个点都是同时向外拓展一步，并且只拓展一次。那么我们将其速度看作1步/次。每个点都向外探索一次。那么此时我们的次数可以类比为时间，由此每条路的速度和时间都是一样的，因此每条路的路程都是一样的。

而各个点都是从起点开始扩散的。我们看下面的例子：

某时刻，绿色线到达了B点，此时各个路线的长度都是L，那么接下来再走的话，蓝色线的路程和黄色线的路程只会更长，因此其再到达B点的时候，必不如绿色线近。== 因此，第一次到达某个点的路线，就是最短的路线 ==

由于mark数组中的点，踩过一次后，就不许再经过了。于是，我们惊奇地发现，每个点记录的路程都是从起点到该点的最短路！！！