2022MathorCup赛题B

以下所有文字均基于作者的实际经验，并不具有完全的合理性，请谨慎参考

目录

一、问题分析

（一）问题一

（二）问题二

二、预处理

（一）训练集预处理

（二）测试集预处理

三、相关性分析

（一）线性相关性

 （二）非线性相关性

 四、结果预测

五、材料源码

---

一、问题分析

首先要明白要解决一个什么问题，在原本的文档中，有六个数据集，分别是附件一语音业务满意度、附件二上网业务满意度、附件三语音业务满意度预测、附件四上网业务满意度预测、附件五字段说明、result预测集。

对于语音业务来说，里面有语音通话整体满意度、网络覆盖与信号强度、语音通话清晰度、语音通话稳定性四个标签属性，且这四个属性的取值都是0-10的离散取值。这就说明，这可能是一个典型的十分类问题，且需要对这四个属性分别建立分类器，也就是单单一个语音业务就是四个十分类。

同样，对于上网业务来说，里面有手机上网整体满意度、网络覆盖与信号强度、手机上网速度、手机上网稳定性四个标签属性，且这四个属性的取值都是0-10的离散取值。同样，这可能是典型的四个十分类。

以上为我们观察数据结构的基本判断，然后我们再关注文档中的要求。

（一）问题一

问题一需要我们找到语音业务和上网业务中对这八个评分影响最大的因素，那其实就是相关性的分析，也就是找到两种业务中剩余属性中对上面提到的八个标签属性影响最大的属性，因为显而易见，出题方希望找到影响他们业务最大的相关因素，从而对该服务进行重点关注。（本质是相关性分析，可能可以使用关联规则挖掘的相关工具）

（二）问题二

问题二需要我们根据自己建立的模型和预测集得出预测结果，然后填入result表格，那就根据建模情况进行预测即可。

二、预处理

结果的预测好坏跟数据的前期处理非常相关

首先需要关注训练集和预测集属性的异同，从中分析实际有用的属性。结合到本赛题的实际情况，需要关注附件五字段说明中对各属性的描述。

这里发现训练集中存在预测集中没有的属性，这种情况基本很少发生，但是本赛题出现，就可以直接删除。这里比如语音业务中的“重定向次数”，这个属性在预测集中并没有存在。

第二种发现预测集中存在训练集中没有的属性，这种情况基本也不会发生，所以建议仔细比对各属性的实际含义，然后考虑对训练集的属性进行删除或者合并或者其它操作。比如语音业务中，训练集中存在“家宽投诉”和“资费投诉”两个属性，但是预测集中是“是否投诉”属性，那么可以把家宽投诉和资费投诉合并为是否投诉，这里就需要对每个样本的两个属性取并集。

（一）训练集预处理

1、删除预测集中不存在的属性

2、删除无关属性。例如本题中的用户id

3、按照题目要求填充空缺值。这里是按照附件五字段说明填充空缺值，比如语音业务中的“是否关怀用户”

4、空缺值、异常值填充。某些属性下样本的值与其它样本与众不同，比如其它都是float类型，然后异常显示为string类型，这种一般用值填充。

连续值的话一般用均值填充，离散值的话可以用众值或“其它”填充，前提是有“其他”这个值，很多时候，离散值都是string类型（可能表格有“其他选项”，生活中调研问卷也会给出这样的选项）。或者可以选择直接把该样本删除，这样做的好处是可以提高拟合度，但是相反就丢失了一些可能重要的信息。（意思就是取舍，看你是愿意为了提高拟合度舍弃部分信息，还是为了模型考虑更加周全而降低你的准确率）

这里建议单独查看这些异常值样本的情况，如果数量相对于整体样本特别少，或者此样本还存在其他属性上的问题（比如好几个属性值异常，好几个属性值缺失），都建议删除。

5、列索引重整化。为了后面属性编码方便，建议进行这个操作，这个操作可以重新把属性的索引下标进行排列。

6、离散属性编码。某些属性可能是string类型，不利于模型训练，这里可以使用一些编码方式，比如one-hot编码、映射编码等多种编码方式。

7、归一化、标准化。这一步的操作就是让特征向量变得更加趋近中心化，更呈现出某种分布，某些模型空间性要求比较高，这一步就非却不可，比如SVM。但是对于一些通过离散方式训练的模型就显得比较多余，甚至会因此影响模型，比如决策树，但是Cart树和C4.5克服了连续属性的影响，这里需要仔细斟酌。

注意：数据属性取值要么是连续的，要么是离散的，某些模型需要连续属性，某些模型需要离散属性，但连续属性能适应大部分模型，所以不存在连续属性或离散属性的好坏，对属性进行连续或离散的变换能够更好拟合模型，但同时也会让属性失去一些信息，所以需要抉择和判断。数据连续化比较容易处理，数据离散化通常需要用到分箱方法，而且很需要能力和经验，如何进行分箱也是一门学问。

（二）测试集预处理

基本操作同训练集预处理相同，可能由于某些属性不同需要进行个别调整。

以下为语音业务训练集的预处理部分代码

# coding=utf-8
import os
import numpy as np
from sklearn.preprocessing import StandardScaler
import pandas as pd
# 填充空缺值
def my_fill(data):
    # print(data.isnull().sum()) #查看空值

    # 测试集中没有相关属性
    data.drop(['重定向次数', '重定向驻留时长','语音方式','是否去过营业厅','ARPU（家庭宽带）','是否实名登记用户'],axis=1,inplace=True)

    # 删除无关属性
    data.drop(['用户描述', '用户id', '用户描述.1'], axis=1,inplace=True)

    # 按照表格要求填充空缺值
    data['是否关怀用户'].fillna('否',inplace=True)

    # 该属性下的样本缺失值较多，且样本量较少直接删除（其它属性也缺失）
    drop1 = data[data["是否4G网络客户（本地剔除物联网）"].isnull()].index.tolist()
    data.drop(labels=drop1,axis=0,inplace=True)

    # 该属性下的样本格式错误，无法读取，导致变为0，由于是连续值，用均值代替
    drop2 = data[data["外省流量占比"].isnull()].index.tolist()
    temp_data = data.drop(labels=drop2,axis=0,inplace=False)
    fill = temp_data["外省流量占比"].unique()
    data["外省流量占比"].fillna(np.mean(fill),inplace=True)

    # 替换异常值0变为其他，这些特征其他属性没问题，在这里全是string类型的值里是0，可能是异常
    data['终端品牌'].replace(0, '其他', inplace=True)

    # 将两个投诉变为合并为一个投诉
    cnt1 = data['家宽投诉']+data['资费投诉']
    data['家宽投诉'] = cnt1
    data.drop(['资费投诉'],axis=1,inplace=True)
    data.rename(columns={'家宽投诉':'是否投诉'},inplace=True)
    data['是否投诉'] = data['是否投诉'].apply(lambda x: '否' if x == 0 else '是')

    # 将两个欠费变为合并为一个欠费
    cnt2 = data['当月欠费金额'] + data['前第3个月欠费金额']
    data['当月欠费金额'] = cnt2
    data.drop(['前第3个月欠费金额'], axis=1, inplace=True)
    data.rename(columns={'当月欠费金额': '是否不限量套餐到达用户'}, inplace=True)
    data['是否不限量套餐到达用户'] = data['是否不限量套餐到达用户'].apply(lambda x: '否' if x == 0 else '是')

    #重整行索引，为后面编码提供方便
    data.reset_index(drop=True,inplace=True)
    return data

# 属性编码
def my_encode(data):
    # 映射（层次）编码，对字符串属性进行特征编码
    code4 = {
        '2G':0,
        '4G':1,
        '5G':2
    }
    data['4\\5G用户'] = data['4\\5G用户'].map(code4)

    # 映射编码
    code6 = {
        '否':0,
        '是':1
    }
    data['是否关怀用户'] = data['是否关怀用户'].map(code6)
    data['是否4G网络客户（本地剔除物联网）'] = data['是否4G网络客户（本地剔除物联网）'].map(code6)
    data['是否5G网络客户'] = data['是否5G网络客户'].map(code6)
    data['是否投诉'] = data['是否投诉'].map(code6)
    data['是否不限量套餐到达用户'] = data['是否不限量套餐到达用户'].map(code6)

    # 映射编码
    val = data['终端品牌'].unique()
    labels = [i for i in range(0,len(val))]
    code14 = dict(zip(val,labels))
    data['终端品牌'] = data['终端品牌'].map(code14)

    #映射编码
    val = data['终端品牌类型'].unique()
    labels = [i for i in range(0, len(val))]
    code15 = dict(zip(val, labels))
    data['终端品牌类型'] = data['终端品牌类型'].map(code15)

    # 映射编码
    val = data['客户星级标识'].unique()
    labels = [i for i in range(0, len(val))]
    code18 = dict(zip(val, labels))
    data['客户星级标识'] = data['客户星级标识'].map(code18)

    return data
def scalelize(data):
    scal = StandardScaler()
    new_data = scal.fit_transform(data)
    return new_data

data = pd.read_excel('../附件1语音业务用户满意度数据.xlsx')
data_fill = my_fill(data) #填充后的数据
data_encode = my_encode(data_fill) #编码后的数据

y1 = data_encode['语音通话整体满意度'] #总标签1
y2 = data_encode['网络覆盖与信号强度'] #标签2
y3 = data_encode['语音通话清晰度'] #标签3
y4 = data_encode['语音通话稳定性'] #标签4
y_all = pd.concat([y1,y2],axis=1)
y_all = pd.concat([y_all,y3],axis=1)
y_all = pd.concat([y_all,y4],axis=1)

# 去除标签的特征
x_dataframe = data_encode.drop(['语音通话整体满意度', '网络覆盖与信号强度','语音通话清晰度','语音通话稳定性'], axis=1)
x = pd.DataFrame(scalelize(x_dataframe))
x.columns = ['是否遇到过网络问题', '居民小区', '办公室', '高校', '商业街', '地铁', '农村', '高铁', '其他，请注明', '手机没有信号', '有信号无法拨通', '通话过程中突然中断', '通话中有杂音、听不清、断断续续', '串线', '通话过程中一方听不见', '其他，请注明.1', '脱网次数', 'mos质差次数', '未接通掉话次数', '是否投诉', '4\\5G用户', '是否关怀用户', '套外流量（MB）', '是否4G网络客户（本地剔除物联网）', '套外流量费（元）', '外省语音占比', '语音通话-时长（分钟）', '省际漫游-时长（分钟）', '终端品牌', '终端品牌类型', '当月ARPU', '当月MOU', '前3月ARPU', '前3月MOU', '外省流量占比', 'GPRS总流量（KB）', 'GPRS-国内漫游-流量（KB）', '是否5G网络客户', '客户星级标识', '是否不限量套餐到达用户']

# 导出
writer = pd.ExcelWriter("./1_train.xlsx")
x.to_excel(writer,index=False)
writer.save()

writer1 = pd.ExcelWriter("./1_train_label.xlsx")
y_all.to_excel(writer1,index=False)
writer1.save()

三、相关性分析

相关性分析可以理解为找多个属性之间的相似度，一些书本上记录了许多相关系数可以进行参考，这里仅给出部分

（一）线性相关性

最典型的就是皮尔逊相关系数，也就是通过协方差的方式得出每个属性之间的相关度，然后可以用协方差矩阵和热力图直观看出属性之间的相关影响。例如下图

 （二）非线性相关性

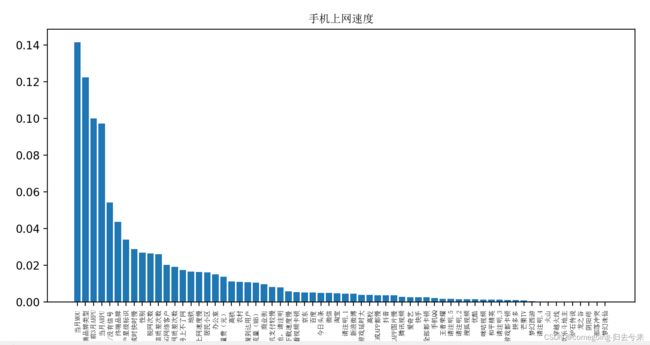
这里最典型的就是信息增益，通过决策树模型得出每个属性对标签属性的信息增益。例如下图

 四、结果预测

针对这个赛题，其实我们通过皮尔逊相关系数发现其线性相关度较小，那么通过决策树既可以得到相关度同时也可以对结果进行预测

五、材料源码

github（仅代码）：

GitHub - comegoing/2022mathorcup

百度网盘（完整）：

链接：https://pan.baidu.com/s/1efuzvLE7RTV_U4TZA9KnKw?pwd=2023 
提取码：2023