量子退火Python实战（5）：PyQUBO高级攻略 MathorCup2023最后助攻

---

---

前言

今天发布有点晚了，希望能给大家最后一点帮助。希望大家比赛结束有兴趣的也能接着研究，提出问题。

---

参考此文：https://www.fruity-floral.com/programming/pyqubotips/

一、高次项怎么用PyQUBO直接编程？

下面是最简单的一个立方项，有$x,y,z$三项。

1. 三次项示例

2. PyQUBO实现

#常量系数
alpha = Placeholder("alpha")
#变量
x, y, z = Binary("x"), Binary("y"), Binary("z")
#目标函数
H = alpha * x * y * z
#PyQUBO自动编译
model = H.compile()
#生成QUBO
QUBO, offset = model.to_qubo(feed_dict = {"alpha": 7})
#打印变量列表
print(model.variables)
#打印QUBO
print(QUBO)

结果如下：

['x', 'y', 'z', '0*1']
{('x', 'x'): 0.0, ('y', 'y'): 0.0, ('z', 'z'): 0.0, ('y', '0*1'): -10.0, ('z', '0*1'): 7.0, ('0*1', '0*1'): 15.0, ('x', '0*1'): -10.0, ('x', 'y'): 5.0}

最后的二次多项式结果就是下面的式子：$S=5$

超高次项，大家用for循环就能实现。

二、不等式怎么用PyQUBO实现？

参考此文：https://www.fruity-floral.com/programming/pyqubotips/

1. 不等式的例子

考虑将以下不等式定义的约束合并到目标函数中。

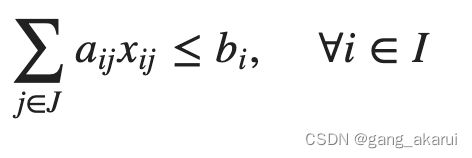
这里又个新概念：松弛变量(slack variable) 。
就是0～$b_i$之间的整数列表。定义为$y_i$。
至于为什么，有兴趣的可以想一下，今天想提前发布文章，之后更新。

2. PyQUBO实现

from pyqubo import Array,Sum,Constraint,Placeholder,LogEncInteger

#创建松弛变量
y = []
for i in range(n):
    y.append(LogEncInteger(f"y{i}",lower=0,upper=JOB_SIZE*2))
#约束定义    
H2 = Sum(0,n,lambda i: Constraint(Sum(0,m,lambda j: x[(i,j)]*a[i,j] +y[i] - b[i])**2,f"Agent Resource {i}"))

总结

两个例子可以具体展开讲，今天想发布实用简略版。大家有问题接着留言。