手把手教你Temporal Fusion Transformer——Pytorch实战

建立了一个关于能源需求预测的端到端项目：
如何为 TFT 格式准备我们的数据。
如何构建、训练和评估 TFT 模型。
如何获取对验证数据和样本外预测的预测。
如何使用built-in model的可解释注意力机制计算特征重要性、季节性模式和极端事件鲁棒性。

什么是Temporal Fusion Transformer （TFT）

Temporal Fusion Transformer （TFT） 是一个基于变压器的模型，它利用自我注意力来捕捉多个时间序列的复杂时间动态。

TFT 支持：

Multiple time series:：我们可以在数千个单变量或多变量时间序列上训练 TFT 模型。
Multi-Horizon Forecasting： 该模型输出一个或多个目标变量的多步预测，包括预测区间。
Heterogeneous features： TFT 支持多种类型的特征，包括时变和静态外生变量。
Interpretable predictions： 预测可以根据可变的重要性和季节性来解释。
其中一个特征是Temporal Fusion Transformer独有的。

扩展时间序列数据格式

TFT 支持各种类型的功能:
Time-varying known
Time-varying unknown
Time-invariant real
Time-invariant categorical

假设我们必须预测 3 种产品的销售情况。num sales是目标变量。或 CPI index or the number of visitors是时变的未知特征，因为它们仅在预测时间内已知。但是，并且holidays和special days是随时间变化的已知事件

product id是一个时不变（静态）分类特征。其他数值且不随时间变化的特征，例如yearly_revenue可以归类为时不变实数。

在进入我们的项目之前，我们将首先展示一个关于如何将数据转换为扩展时间序列格式的迷你教程。

时间序列数据集函数TimeSeriesDataSet Function

在本教程中，我们使用 PyTorch 预测库和 PyTorch Lightning 中的模型：TemporalFusionTransformer

pip install torch pytorch-lightning pytorch_forecasting

整个过程涉及3件事：

1. 使用我们的时间序列数据创建pandas数据帧。
2. 将数据帧包装到TimeSeriesDataset实例中。
3. 将我们的TimeSeriesDataset实例传递给TemporalFusionTransformer.

TimeSeriesDataset非常有用，因为它可以帮助我们指定特征是时变的还是静态的。另外，它是TemporalFusionTransformer唯一接受的格式。
让我们创建一个最小的训练数据集来展示 TimeSeriesDataset 的工作原理：

import numpy as np
import pandas as pd
from pytorch_forecasting import TimeSeriesDataSet

sample_data = pd.DataFrame(
    dict(
        time_idx=np.tile(np.arange(6), 3),
        target=np.array([0,1,2,3,4,5,20,21,22,23,24,25,40,41,42,43,44,45]),
        group=np.repeat(np.arange(3), 6),
        holidays = np.tile(['X','Black Friday', 'X','Christmas','X', 'X'],3),
    )
)
sample_data

代码创建了一个名为 sample_data 的数据框，使用了 pandas 和 numpy 库。数据框有4列：time_idx，target，group 和 holidays。 time_idx 列包含6个时间索引，重复3次。 target 列包含每个时间索引增加1的值，并在每6个时间索引后重置。 group 列包含3个组，重复6次。 holidays 列包含假期名称和 ‘X’ 值的重复序列。

我们应该按以下方式格式化数据：每个彩色框代表一个不同的时间序列，由其group值表示。

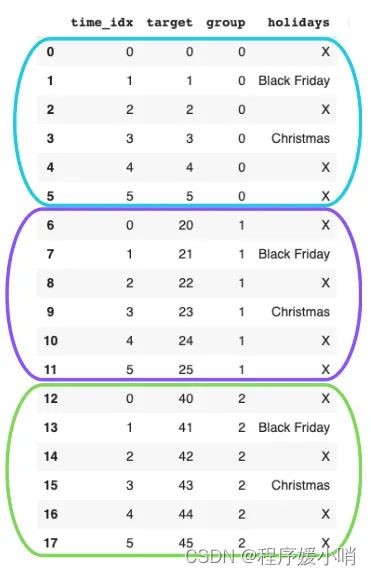
数据帧中最重要的列是time_idx — 它决定了样本的顺序。如果没有缺失观测值，则每个时间序列的值应增加 +1。

接下来，我们将数据帧包装到TimeSeriesDataset实例中：

create the time-series dataset from the pandas df

dataset = TimeSeriesDataSet(
    sample_data,
    group_ids=["group"],
    target="target",
    time_idx="time_idx",
    max_encoder_length=2,
    max_prediction_length=3,
    time_varying_unknown_reals=["target"],
    static_categoricals=["holidays"],
    target_normalizer=None
)

代码使用 pytorch_forecasting 库中的 TimeSeriesDataSet 类创建了一个名为 dataset 的时间序列数据集。数据集使用 sample_data 数据框作为输入，并指定了以下参数：

group_ids：指定用于分组的列，这里是 group 列。
target：指定目标列，这里是 target 列。
time_idx：指定时间索引列，这里是 time_idx 列。
max_encoder_length：定义lookback period，指定编码器的最大长度，这里是2。
max_prediction_length：指定预测的最大长度，指定将要预测的数据点数，这里是3。
time_varying_unknown_reals：指定未知实数的时间变化列，这里是 target 列。
static_categoricals：指定静态分类列，这里是 holidays 列。
target_normalizer：指定目标正则化器，这里为None。

在我们的例子中，我们回顾过去的 3 个时间步长以输出 2 个预测。
TimeSeriesDataset 实例现在用作数据加载器。

让我们打印一个批次并检查我们的数据将如何传递给 TFT：

pass the dataset to a dataloader

dataloader = dataset.to_dataloader(batch_size=1)

代码使用 to_dataloader 方法将 dataset 转换为一个数据加载器，命名为 dataloader。这个方法接受一个参数 batch_size，它指定了每个批次的大小。在这里，你将批次大小设置为1。

数据加载器可用于在训练过程中迭代地加载数据。你可以使用它来训练模型或进行预测。

load the first batch

x, y = next(iter(dataloader))
print(x['encoder_target'])
print(x['groups'])
print('\n')
print(x['decoder_target'])

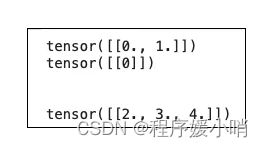
此批处理包含来自第一个时间序列 （group 0） 的训练值[0,1]和测试值[2,3,4]。

如果重新运行此代码，将获得不同的值，因为默认情况下数据是随机排列的。

需求能源预测

使用UCI的ElectricLoadDiagrams20112014数据集。

此数据集包含 370 个客户端/使用者的电源使用情况（以 KW 为单位），
频率为 15 分钟。
数据跨度为4年（2011-2014年）。

一些消费者是在2011年之后创建的，因此他们的用电量最初为零。

我们根据原论文代码进行数据预处理：

• 按小时聚合我们的目标变量power_usage。
• 查找电量为非零的每个时间序列的最早日期。
• 创建新要素 ： month，day，hour，day_of_week。
• 选择介于2014–01–01和2014–09–07之间的所有日期。

下载数据 Download Data

wget https://archive.ics.uci.edu/ml/machine-learning-databases/00321/LD2011_2014.txt.zip
!unzip LD2011_2014.txt.zip

Data Preprocessing

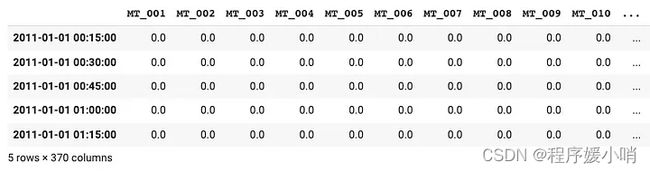
data = pd.read_csv('LD2011_2014.txt', index_col=0, sep=';', decimal=',')
data.index = pd.to_datetime(data.index)
data.sort_index(inplace=True)
data.head(5)

每列代表一个使用者。大多数power_usage初始值为 0。

接下来，我们聚合到每小时数据。由于模型的大小和复杂性，我们仅在 5 个使用者上训练模型（对于具有非零值的使用者）。

data = data.resample('1h').mean().replace(0., np.nan)
earliest_time = data.index.min()
df=data[['MT_002', 'MT_004', 'MT_005', 'MT_006', 'MT_008' ]]

现在，我们为 TimeSeriesDataset 格式准备数据集。请注意，每列表示不同的时间序列。因此，我们“融化”了数据帧，以便所有时间序列都垂直堆叠而不是水平堆叠。在此过程中，我们创建了新功能。

df_list = []

for label in df:

    ts = df[label]
    start_date = min(ts.fillna(method='ffill').dropna().index)
    end_date = max(ts.fillna(method='bfill').dropna().index)

    active_range = (ts.index >= start_date) & (ts.index <= end_date)
    ts = ts[active_range].fillna(0.)

    tmp = pd.DataFrame({'power_usage': ts})
    date = tmp.index

    tmp['hours_from_start'] = (date - earliest_time).seconds / 60 / 60 + (date - earliest_time).days * 24
    tmp['hours_from_start'] = tmp['hours_from_start'].astype('int')
  
    tmp['days_from_start'] = (date - earliest_time).days
    tmp['date'] = date
    tmp['consumer_id'] = label
    tmp['hour'] = date.hour
    tmp['day'] = date.day
    tmp['day_of_week'] = date.dayofweek
    tmp['month'] = date.month

    #stack all time series vertically
    df_list.append(tmp)

time_df = pd.concat(df_list).reset_index(drop=True)

# match results in the original paper
time_df = time_df[(time_df['days_from_start'] >= 1096)
                & (time_df['days_from_start'] < 1346)].copy()

for label in df 这一行代码的目的是遍历DataFrame df 中的每一列。在这个循环中，label 变量表示当前正在处理的列的名称。这样，代码可以对每一列数据进行相同的处理，而不需要重复编写相同的代码。
码通过用0填充缺失值，计算时间序列的活动范围，并提取诸如起始小时数、起始天数、日期、消费者ID、小时、天、星期几和月份等特征来处理每个时间序列数据。最后，它将所有处理过的时间序列数据垂直堆叠，并过滤结果DataFrame以匹配原始论文中的结果。

处理一个包含多个标签时间序列数据的DataFrame df。代码计算每个标签的开始和结束日期，用0填充缺失值，并根据日期索引创建几个新列。最后，它将所有处理过的时间序列连接成一个DataFrame time_df，并根据days_from_start列过滤行。

最终预处理的数据帧称为time_df 。让我们打印它的内容：

现在，time_df采用 TimeSeriesDataset 的正确格式。正如您现在所猜到的，由于粒度是每小时的，因此变量hours_from_start将是时间索引。

探索性数据分析

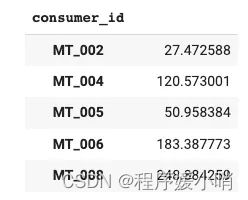
5 个使用者/时间序列的选择不是随机的。每个时间序列具有不同的属性，例如平均值：power usage

time_df[[‘consumer_id’,’power_usage’]].groupby(‘consumer_id’).mean()

让我们绘制每个时间序列的第一个月：

没有明显的趋势，但每个时间序列的季节性和幅度略有不同。我们可以进一步试验和检查平稳性、信号分解等，但在我们的例子中，我们只关注模型构建方面。

另外，请注意，其他时间序列预测方法（如 ARIMA）必须满足一些要求（例如，时间序列必须首先变得平稳）。使用 TFT，我们可以保持数据不变。

创建数据加载器

在此步骤中，我们将time_df传递到TimeSeriesDataSet格式，该格式非常有用，因为：

它使我们免于编写自己的数据加载器。
我们可以指定 TFT 将如何处理数据集的特征。
我们可以轻松地规范化我们的数据集。在我们的例子中，归一化是强制性的，因为所有时间序列的量级都不同。因此，我们使用 GroupNormalizer 单独规范化每个时间序列。
我们的模型使用一周 （7*24） 的回溯窗口来预测未来 24 小时的用电量。

另请注意，hours_from_start既是时间索引，也是时变特征。power_usage是我们的目标变量。为了演示，我们的验证集是最后一天：

#Hyperparameters
#batch size=64
#number heads=4, hidden sizes=160, lr=0.001, gr_clip=0.1

max_prediction_length = 24
max_encoder_length = 7*24
training_cutoff = time_df["hours_from_start"].max() - max_prediction_length

training = TimeSeriesDataSet(
    time_df[lambda x: x.hours_from_start <= training_cutoff],
    time_idx="hours_from_start",
    target="power_usage",
    group_ids=["consumer_id"],
    min_encoder_length=max_encoder_length // 2, 
    max_encoder_length=max_encoder_length,
    min_prediction_length=1,
    max_prediction_length=max_prediction_length,
    static_categoricals=["consumer_id"],
    time_varying_known_reals=["hours_from_start","day","day_of_week", "month", 'hour'],
    time_varying_unknown_reals=['power_usage'],
    target_normalizer=GroupNormalizer(
        groups=["consumer_id"], transformation="softplus"
    ),  # we normalize by group
    add_relative_time_idx=True,
    add_target_scales=True,
    add_encoder_length=True,
)


validation = TimeSeriesDataSet.from_dataset(training, time_df, predict=True, stop_randomization=True)

# create dataloaders for  our model
batch_size = 64 
# if you have a strong GPU, feel free to increase the number of workers  
train_dataloader = training.to_dataloader(train=True, batch_size=batch_size, num_workers=0)
val_dataloader = validation.to_dataloader(train=False, batch_size=batch_size * 10, num_workers=0)

这段代码创建了一个 TimeSeriesDataSet 对象，用于训练时间序列模型。它使用 time_df 中 hours_from_start 列的值小于等于 training_cutoff 的数据作为训练数据。TimeSeriesDataSet 对象需要指定多个参数，包括时间索引、目标变量、分组变量、编码器长度、预测长度、静态分类变量、已知实值变量、未知实值变量和目标正则化器等。这些参数用于定义时间序列模型的输入和输出格式。

静态分类变量、已知实值变量和未知实值变量都是时间序列模型的输入特征。

静态分类变量（static_categoricals）是指在整个时间序列中不会改变的分类变量。例如，在这段代码中，consumer_id 是一个静态分类变量，因为每个消费者的ID在整个时间序列中都不会改变。

已知实值变量（time_varying_known_reals）是指在预测时已知的实值变量。例如，在这段代码中，hours_from_start、day、day_of_week、month 和 hour 都是已知实值变量，因为它们在预测时都是已知的。

未知实值变量（time_varying_unknown_reals）是指在预测时未知的实值变量。例如，在这段代码中，power_usage 是一个未知实值变量，因为它是我们要预测的目标变量。

validation = TimeSeriesDataSet.from_dataset(training, time_df, predict=True, stop_randomization=True)

创建了验证数据集，基于训练数据集并指定了预测标志，停止随机化等参数。

batch_size = 64 
train_dataloader = training.to_dataloader(train=True, batch_size=batch_size, num_workers=0)
val_dataloader = validation.to_dataloader(train=False, batch_size=batch_size * 10, num_workers=0)

定义了批次大小和数据加载器，用于训练和验证模型。在这里，训练数据集和验证数据集分别被转换为相应的数据加载器对象，每个对象都包括批次大小和工作进程数。

基线模型

接下来，几乎每个人都忘记的步骤：基线模型。特别是在时间序列预测中，您会惊讶于朴素预测器甚至优于更高级的模型的效果！

作为朴素基线，我们预测前一天的电源使用曲线：

actuals = torch.cat([y for x, (y, weight) in iter(val_dataloader)])
baseline_predictions = Baseline().predict(val_dataloader)
(actuals - baseline_predictions).abs().mean().item()

# ➢25.139617919921875

训练TFT

我们可以使用PyTorch Lightning中熟悉的Trainer界面来训练我们的TFT模型。

请注意以下事项：

我们使用 EarlyStop 回调来监视验证丢失。
我们使用 Tensorboard 来记录我们的训练和验证指标。
我们的模型使用分位数损失 — 一种特殊类型的损失，可帮助我们输出预测区间。有关分位数损失函数的更多信息，请查看本文。
我们使用 4 个注意力头，就像原始论文一样。
现在，我们已准备好构建和训练模型：

early_stop_callback = EarlyStopping(monitor="val_loss", min_delta=1e-4, patience=5, verbose=True, mode="min")
lr_logger = LearningRateMonitor()  
logger = TensorBoardLogger("lightning_logs")  

trainer = pl.Trainer(
    max_epochs=45,
    accelerator='gpu', 
    devices=1,
    enable_model_summary=True,
    gradient_clip_val=0.1,
    callbacks=[lr_logger, early_stop_callback],
    logger=logger)

tft = TemporalFusionTransformer.from_dataset(
    training,
    learning_rate=0.001,
    hidden_size=160,
    attention_head_size=4,
    dropout=0.1,
    hidden_continuous_size=160,
    output_size=7,  # there are 7 quantiles by default: [0.02, 0.1, 0.25, 0.5, 0.75, 0.9, 0.98]
    loss=QuantileLoss(),
    log_interval=10, 
    reduce_on_plateau_patience=4)

trainer.fit(
    tft,
    train_dataloaders=train_dataloader,
    val_dataloaders=val_dataloader)

加载并保存最佳模型

best_model_path = trainer.checkpoint_callback.best_model_path
print(best_model_path)
best_tft = TemporalFusionTransformer.load_from_checkpoint(best_model_path)

不要忘记保存您的模型。虽然我们可以pickle 它，但最安全的选择是直接save the best epoch：

!zip  -r model.zip lightning_logs/lightning_logs/version_1/*

要再次加载模型，请解压缩模型.zip并执行以下操作 — 只需记住最佳模型路径：

#load our saved model again
!unzip model.zip
best_model_path='lightning_logs/lightning_logs/version_1/checkpoints/epoch=8-step=4212.ckpt'
best_tft = TemporalFusionTransformer.load_from_checkpoint(best_model_path)

查看Tensorboard

仔细看看使用Tensorboard的训练和验证曲线：

# Start tensorboard
%load_ext tensorboard
%tensorboard - logdir lightning_logs

模型评估

获取验证集的预测并计算平均 P50（分位数中位数）损失：

actuals = torch.cat([y[0] for x, y in iter(val_dataloader)])
predictions = best_tft.predict(val_dataloader)

#average p50 loss overall
print((actuals - predictions).abs().mean().item())
#average p50 loss per time series
print((actuals - predictions).abs().mean(axis=1))

# ➢6.686748027801514
# ➢tensor([ 1.5708,  8.7656,  1.9709,  8.1660, 12.9604])

最后 2 个时间序列的损失稍高，因为它们的相对幅度也很高。

验证数据的绘图预测

如果我们传递 predict（） 方法，我们会得到更多信息，包括对所有七个分位数的预测。我们还可以访问注意力值（稍后会详细介绍）。mode=raw

仔细看看变量：raw_predictions

#Take a look at what the raw_predictions variable contains

raw_predictions, x = best_tft.predict(val_dataloader, mode="raw", return_x=True)
print(raw_predictions._fields)
# ('prediction', 
# 'encoder_attention', 
# 'decoder_attention', 
# 'static_variables', 
# 'encoder_variables', 
# 'decoder_variables', 
# 'decoder_lengths', 
# 'encoder_lengths')

print('\n')
print(raw_predictions['prediction'].shape)
#torch.Size([5, 24, 7])

# We get predictions of 5 time-series for 24 days.
# For each day we get 7 predictions - these are the 7 quantiles:
#[0.02, 0.1, 0.25, 0.5, 0.75, 0.9, 0.98]
# We are mostly interested in the 4th quantile which represents, let's say, the 'median loss'
# fyi, although docs use the term quantiles, the most accurate term are percentiles

这段代码使用 TensorFlow Time Series (TFT) 模型对验证集数据进行预测。具体来说，它使用 predict() 函数来生成所有验证数据点的原始预测值。

val_dataloader 是一个 PyTorch 的 DataLoader 对象，包含用于验证的时间序列数据。mode 参数设置为 “raw”，表示要返回原始预测值，而不是已处理过的值。return_x=True 参数表示返回时间索引，即每个预测值对应的时间戳。

predict() 函数返回原始预测值 raw_predictions 和与其对应的时间索引值 x。这些预测值和时间索引可以用于后续的分析、可视化或其他处理。

我们使用 plot_prediction（） 来创建我们的绘图。当然，您可以制作自己的自定义绘图 — plot_prediction（） 具有添加注意力值的额外好处。

注意：我们的模型一次性预测接下来的 24 个数据点。这不是一个滚动预测方案，其中模型每次预测单个值并将所有预测“拼接”在一起。

我们为每个消费者创建一个图（总共 5 个）。

for idx in range(5):  # plot all 5 consumers
    fig, ax = plt.subplots(figsize=(10, 4))
    best_tft.plot_prediction(x, raw_predictions, idx=idx, add_loss_to_title=True,ax=ax)

这段代码是使用循环语句，对 5 个不同的消费者进行预测结果的绘制。每个消费者的预测结果都将绘制在一个单独的图表中。

对于每个循环迭代，使用 matplotlib 库创建一个 Figure 对象和一个 Axes 对象，并将其大小设置为 (10, 4)。然后，使用 TFT 模型中的 plot_prediction() 函数，将该消费者的预测结果绘制到 Axes 对象上。idx 参数指定要绘制的消费者的索引。raw_predictions 包含所有消费者的原始预测值，x 包含所有消费者的时间索引。add_loss_to_title=True 参数将在图表标题中添加损失函数的值。

在循环的每次迭代中，都会绘制一个新的图表，直到循环结束，即绘制了所有消费者的预测结果。

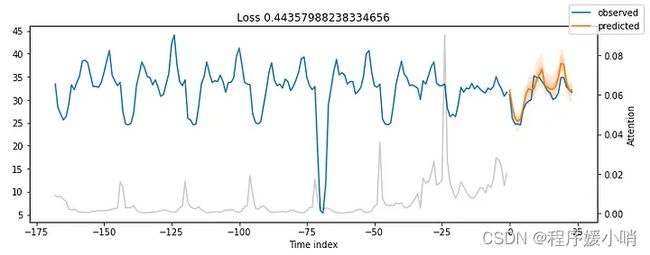
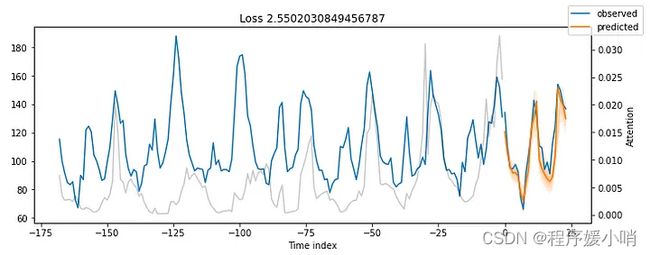
结果令人印象深刻。

我们的时间融合变压器模型能够捕获所有5个时间序列的行为，包括季节性和幅度！

另请注意：

我们没有执行任何超参数调优。
我们没有实现任何花哨的特征工程技术。
在后续部分中，我们将展示如何使用超参数优化来改进模型。

绘制特定时间序列的预测

以前，我们使用参数对验证数据进行预测，该参数迭代数据集中的所有时间序列。我们可以更具体地输出特定时间序列的预测：idx

fig, ax = plt.subplots(figsize=(10, 5))

raw_prediction, x = best_tft.predict(
    training.filter(lambda x: (x.consumer_id == "MT_004") & (x.time_idx_first_prediction == 26512)),
    mode="raw",
    return_x=True,
)
best_tft.plot_prediction(x, raw_prediction, idx=0, ax=ax);

这段代码是用 Python 中的 matplotlib 库创建一个包含一个子图的 Figure 对象，并将其大小设置为 (10, 5)。

接下来，使用 TensorFlow Time Series (TFT) 模型中的 predict() 函数对数据进行预测。training.filter() 函数用于过滤出 consumer_id 为 “MT_004” 且 time_idx_first_prediction 为 26512 的数据，这些数据将被用于预测。mode 参数设置为 “raw”，表示要返回原始预测值，而不是已处理过的值。

predict() 函数返回原始预测值 raw_prediction 和与其对应的时间索引值 x。

最后，使用 TFT 模型中的 plot_prediction() 函数将预测结果绘制在子图上，其中 idx=0 表示仅绘制第一个序列的预测结果，ax=ax 参数表示将绘制结果添加到之前创建的 Figure 对象的子图上。

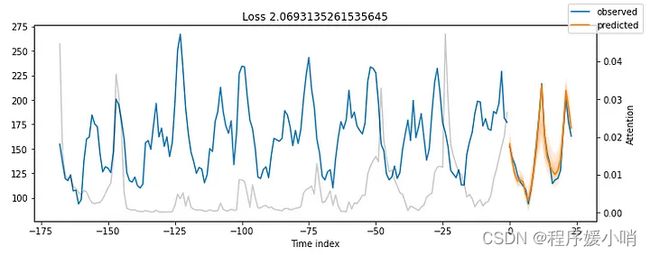
在图 7 中，我们绘制了时间指数 = 004 的MT_26512消费者的前一天。

请记住，我们的时间索引列从 26304 开始，我们可以从 26388 开始获得预测（因为我们之前设置了等于hours_from_startmin_encoder_length=max_encoder_length // 226304 + 168//2=26388

样本外预测

让我们创建样本外预测，超越验证数据的最终数据点 - 即2014–09–07 23:00:00

我们所要做的就是创建一个包含以下内容的新数据帧：

• 数量 = 过去的日期，用作回溯窗口 — TFT 术语中的编码器数据。Nmax_encoder_length
• 我们想要计算预测的未来大小日期 — 解码器数据。max_prediction_length
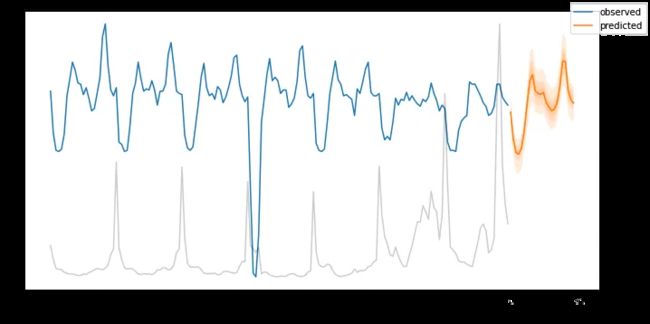
  我们可以为所有 5 个时间序列创建预测，也可以只为一个时间序列创建预测。图 7 显示了消费者MT_002的样本外预测：

#encoder data is the last lookback window: we get the last 1 week (168 datapoints) for all 5 consumers = 840 total datapoints

encoder_data = time_df[lambda x: x.hours_from_start > x.hours_from_start.max() - max_encoder_length]
last_data = time_df[lambda x: x.hours_from_start == x.hours_from_start.max()]

#decoder_data is the new dataframe for which we will create predictions. 
#decoder_data df should be max_prediction_length*consumers = 24*5=120 datapoints long : 24 datapoints for each cosnumer
#we create it by repeating the last hourly observation of every consumer 24 times since we do not really have new test data
#and later we fix the columns

decoder_data = pd.concat(
    [last_data.assign(date=lambda x: x.date + pd.offsets.Hour(i)) for i in range(1, max_prediction_length + 1)],
    ignore_index=True,
)

#fix the new columns
decoder_data["hours_from_start"] = (decoder_data["date"] - earliest_time).dt.seconds / 60 / 60 + (decoder_data["date"] - earliest_time).dt.days * 24
decoder_data['hours_from_start'] = decoder_data['hours_from_start'].astype('int')
decoder_data["hours_from_start"] += encoder_data["hours_from_start"].max() + 1 - decoder_data["hours_from_start"].min()

decoder_data["month"] = decoder_data["date"].dt.month.astype(np.int64)
decoder_data["hour"] = decoder_data["date"].dt.hour.astype(np.int64)
decoder_data["day"] = decoder_data["date"].dt.day.astype(np.int64)
decoder_data["day_of_week"] = decoder_data["date"].dt.dayofweek.astype(np.int64)

new_prediction_data = pd.concat([encoder_data, decoder_data], ignore_index=True)

fig, ax = plt.subplots(figsize=(10, 5))

#create out-of-sample predictions for MT_002
new_prediction_data=new_prediction_data.query(" consumer_id == 'MT_002'")
new_raw_predictions, new_x = best_tft.predict(new_prediction_data, mode="raw", return_x=True)
best_tft.plot_prediction(new_x, new_raw_predictions, idx=0, show_future_observed=False, ax=ax);

图7： MT_002的提前一天预测

可解释预测

准确的预测是一回事，但如今可解释性也很重要。

对于被认为是黑匣子的深度学习模型来说，情况更糟。LIME 和 SHAP 等方法可以提供可解释性（在某种程度上），但不适用于时间序列。此外，它们是外部事后方法，不依赖于特定模型。

时间融合转换器提供三种类型的可解释性：

• 季节性方面： TFT利用其新颖的可解释多头注意力机制来计算过去时间步长的重要性。
• 功能方面： TFT利用其变量选择网络模块来计算每个特征的重要性。
• 极端事件稳健性： 我们可以研究时间序列在罕见事件中的行为
  如果你想深入了解可解释的多头注意力和变量选择网络的内部工作原理，请查看我之前的文章。

季节性可解释性

TFT 探索注意力权重，以了解过去时间步长的时间模式。

之前所有图中的灰线表示注意力分数。再看看那些情节——你注意到什么了吗？图 8 显示了图 7 的结果，还考虑了注意力分数：

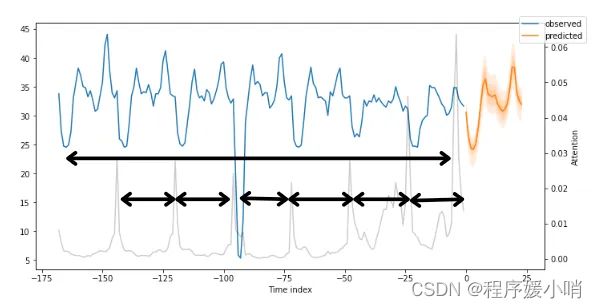
图8： 显示季节性的MT_002提前一天预测

注意力分数揭示了模型输出其预测时这些时间步长的影响程度。小峰值反映了每日季节性，而接近末尾的较高峰值可能意味着每周季节性。

如果我们平均所有时间步长和时间序列的注意力曲线（不仅仅是我们在本教程中使用的 5 个），我们将从 TFT 论文中得到图 9 中的对称形状：

图 9：电力时间模式数据集（来源）)

问题： 这有什么用？我们不能简单地用ACF图、时间信号分解等方法估计季节性模式吗？?

答： 真。然而，研究TFT的注意力权重有额外的优势：

1. 我们可以确认我们的模型捕捉到了序列的明显季节性动态。
2. 我们的模型也可能揭示隐藏的模式，因为当前输入窗口的注意力权重考虑了所有过去的输入。
3. 注意力权重图与自相关图不同：自相关图是指特定序列，而此处的注意力权重通过查看所有协变量和时间序列来关注每个时间步长的影响。

特征可解释性

TFT的变量选择网络组件可以轻松估计特征重要性：

raw_predictions, x = best_tft.predict(val_dataloader, mode="raw", return_x=True)
interpretation = best_tft.interpret_output(raw_predictions, reduction="sum")
best_tft.plot_interpretation(interpretation)

在图 10 中，我们注意到以下内容：

• 和 具有很高的分数，无论是作为过去的观测值还是未来的协变量。原始论文中的基准也得出了相同的结论。hourday_of_week
• 这显然是最具影响力的观测协变量。power_usage
• 这里不是很重要，因为我们只使用 5 个消费者。在TFT论文中，作者使用了所有370个消费者，这个变量更为显着。consumer_id

注意： 如果您的分组静态变量不重要，则很可能您的数据集也可以通过单个分布模型（如 ARIMA）进行同样好的建模。

极端事件检测

时间序列因在罕见事件（也称为冲击）期间容易受到其属性的突然变化而臭名昭著。

更糟糕的是，这些事件非常难以捉摸。想象一下，如果你的目标变量在短时间内变得不稳定，因为协变量静默地改变了行为：

这是一些随机噪声还是隐藏的持久模式，逃脱了我们的模型？

使用 TFT，我们可以分析每个特征在其值范围内的鲁棒性。不幸的是，当前的数据集没有表现出波动性或罕见事件 - 这些更有可能在财务，销售数据等中找到。不过，我们将展示如何计算它们：

#Analysis on the training set

predictions, x = best_tft.predict(train_dataloader, return_x=True)
predictions_vs_actuals = best_tft.calculate_prediction_actual_by_variable(x, predictions)
best_tft.plot_prediction_actual_by_variable(predictions_vs_actuals);

某些特征在验证数据集中不存在其所有值，因此我们仅显示 和 ：hourconsumer_id

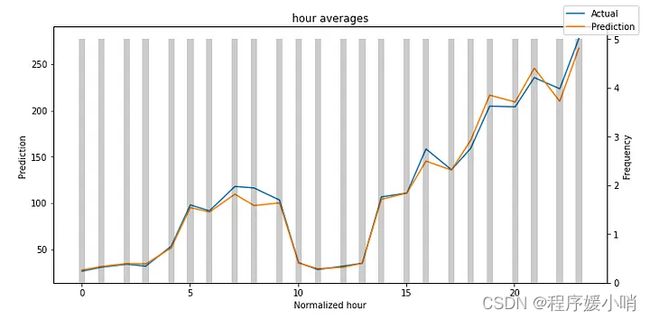
在这两个数字中，结果都是令人鼓舞的。在图 12 中，我们注意到与其他消费者相比，消费者MT_004表现略逊一筹。如果我们将每个消费者的 P50 损失与我们之前计算的平均功耗进行标准化，我们可以验证这一点。

灰色条表示每个变量的分布。我总是做的一件事是找到哪些值的频率较低。然后，我检查模型在这些领域的表现。因此，您可以轻松检测模型是否捕获了罕见事件的行为。

通常，您可以使用此 TFT 功能探测模型的弱点并继续进一步调查。