《LeetCode 热题 HOT 100》——寻找两个正序数组的中位数
本期给大家带来的是是《LeetCode 热题 HOT 100》第四题——寻找两个正序数组的中位数的题目讲解!!!()
本文目录
题意分析
解题思路:
1、直接法 (❌)
2、归并思想 (❌)
①《LeetCode》第88题——合并两个有序数组
3、二分查找(✔️)
整体思想:
题目如下 :
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n))
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
题意分析
首先,我们需要注意的一点就是关于本题时间复杂度的要求,本题要求的时间复杂度为 O(log (m+n)) ,这里一定要特别注意!!
其次,我们来对给出的示例给出解释说明,分析题意:
- 首先对于示例一,题目给出了两个数组——nums1和nums2,两个数组的的合并之后且排好序之后为 【1 2 3】,又因为是 double型 输出,此时它的中位数就是 【2.00000】;
- 其次对于示例二,题目给出了两个数组,数组中的元素分别为【1 2】和【3 4】,此时经过排序,我们得到【1 2 3 4】这样的数组,此时数组的长度为偶数,因此中位数的计算就是【(2 + 3) / 2 = 2.5】
解题思路:
1、直接法 (❌)
首先,大家拿道题,第一种想到的可能就是直接对这两个数组进行合并在进行排序处理,排完序之后紧接着根据数据长度的奇偶性,我们来判断中位数的到底是n/2还是n/2+1:
代码如下:
class Solution {
public:
double findMedianSortedArrays(vector& nums1, vector& nums2) {
vectorarr;
for(auto& e :nums1) {arr.push_back(e);}
for(auto& e :nums2) {arr.push_back(e);}
sort(arr.begin(),arr.end());
int m=arr.size();
if( m % 2 == 0){
return (double)(arr[m/2]+arr[m/2-1]) /2.0;
} else{
return arr[m/2];
}
}
}; 这种做法可以通过但是却不符合提本题的要求,因为它的时间复杂度就为了 O((m+n)log (m+n)),这样做时间复杂度就取决于排序的代价。因此,这种方法我就此忽略。
2、归并思想 (❌)
其实我们在稍加思考,就可以想到一种优化方法。
我们可以联想到归并排序,这个我想大概应该都学过的。我们不用在进行先合并在sorted,我们可以直接把这两个归并为一个已经排序好的数组。此时这就是双指针的算法,时间复杂度此时为O(m+n)。
这个还可以进行优化,我们不需要对全部进行归并操作,因为我们只关心中位数,因此我们可以计算中位数的下标,假设此时中位数的下表为 k,时间复杂度就为O(k),k的取值取决于数组的长度还是,介于(m+n)/2和 (m+n)/2+1。但是此时依然也不能满足我们题意的 log 级别的时间复杂度的要求.
①《LeetCode》第88题——合并两个有序数组
注意:
- 如果大家对这个排序还不熟悉的小伙伴,我在这里就连带还给出了以下题目的讲解,帮助大家认识 归并排序 思想 :
- 《LeetCode》第88题——合并两个有序数组
题目如下:
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:
- 最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
题意分析:
- 首先,根据题意,我们可以知道给出了的数据都是已经排好序的了,因此,这就减少了我们的一步操作;
- 紧接着我们可以发现最终是由nums1返回,因此它的空间都足够大
解题思路:
1、直接法
- 最容易想到的办法无疑是把数组 nums2 的数据元素全部放入到数组 nums1 的尾部,因此题意告诉我们 nums1 的空间大小为【m+n】,然后直接对整个数组进行排序即可。
代码如下:
class Solution {
public:
void merge(vector& nums1, int m, vector& nums2, int n) {
//此时我们选nums1作为 填充数组,把nums2中元素全部插入到nums1中
for(int i=0; i 性能分析:
- 时间复杂度:跟我们上述暴力解《寻找两个正序数组的中位数》一样,此时 时间复杂度为O((m+n)log(m+n))
- 空间复杂度:因为初始时nums1 的空间长度大小已经为 (m+n)了。因此无需在开辟额外的空间对其进行存放操作,因此 空间复杂度为O(1)
2、归并排序思想
- 如果我们仔细观察这到题很明显就是需要利用 二路归并排序 的思想来做。先确定排序后数组的长度,紧接着比较两数组最后的元素的大小,大的放入新数组的最后一位。(因为本题 nums1 数组的长度是 (m+n),所以我们直接覆盖到 nums1 数组之后即可)
图解:
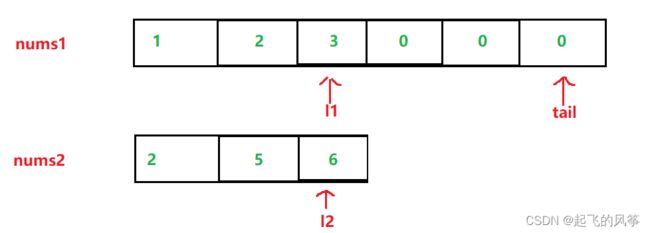
- 开始时如下图所示:
- 第一步,比较 3和6 的大小,此时 6比3 大,因此,把6插入到末尾,同时 l2和tail 两个指针同时往前移动一个位置
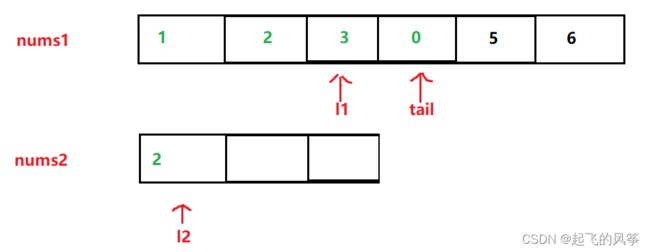
- 第二步:此时在比较 3和5 的大小,发现5比3大,因此同上述操作一样,把 5 插入到 tail指向的位置,同时两个指针在往前移动一位
- 第三步:此时比较 3和2 的大小,发现此时 3比2 大,因此,把3插入到 tail指向的位置,同时 tail和 l1 在往前移动一位
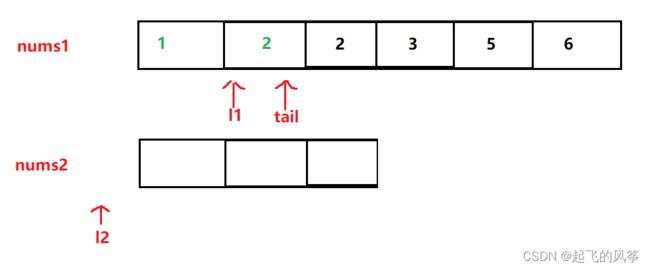
- 第四步:紧接着再次比较 2和2 的大小,发现此时一样大,随便取 l1和l2 位置对应的元素插入到 tail处即可,我们这里是把 l2位置处的 插入到 tail 处。同时移动 l2和tail
- 第五步:此时 nums2的数据 已经处理完毕了,nums1 中还有数据,只需把 nums1 剩余的元素 放入 tail 所指的位置即可,最后完成排序。
代码如下:
class Solution {
public:
void merge(vector& nums1, int m, vector& nums2, int n) {
int l1 = m - 1;
int l2 = n - 1;
int tail = m + n - 1;
while (l1 >= 0 && l2 >= 0)
{
if (nums1[l1] > nums2[l2])
{
nums1[tail--] = nums1[l1--];
}
else
{
nums1[tail--] = nums2[l2--];
}
}
while (l1 >= 0)
{
nums1[tail--] = nums1[l1--];
}
while (l2 >= 0)
{
nums1[tail--] = nums2[l2--];
}
}
}; 性能分析:
- 时间复杂度:指针移动单调递减,最多移动 m+n 次,因此 时间复杂度为 O(m+n)。
- 空间复杂度:直接对数组 nums1 原地修改,不需要额外空间,因此 空间复杂度为O(1)。
温馨小提示:
我们除了从后往前操作之外,还有从前往后操作。这个任务就交给大家了,原理跟上面讲到的一样的!!!
3、二分查找(✔️)
最后,其实我们可以想到,要想实现 log 级别的时间复杂度,最容易想到的就是采用二分查找的思想。
但是二分查找,我们之前学过的都是对一个数组进行二分查找,本题我们这里有两个数组,因此此题的难度我们可以看到标的是 困难。但是也不要害怕,接下来我带大家分析一波
整体思想:
- 更有效的方法是使用二叉搜索,我们可以在两个数组中找到分区点,使得分区点左侧的元素小于右侧的元素。然后,可以通过取左分区的最大值和右分区的最小值来找到中位数!!!
图解:
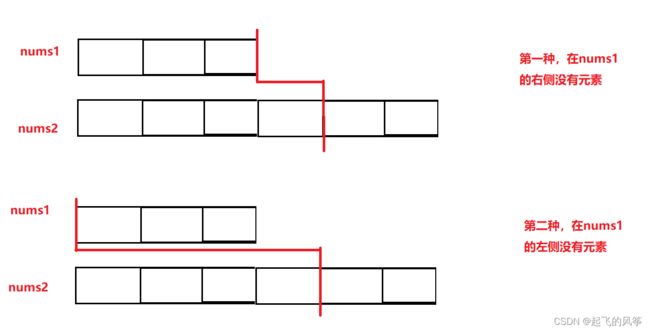
- 分区点不满足的示例:
- 极端情况1:
- 极端情况2:
具体步骤:
- 首先,记录下两个数组的长度大小,以备后序的计算中位数做准备;
- 为了防止分区点的在第二个数组的两侧都有元素,导致出现数组越界的现象。在此实现中,我们首先检查第一个数组的长度是否大于第二个数组的长度。如果是,我们交换数组以确保第一个数组始终是较短的那个数组;
- 然后,我们使用二叉搜索来查找两个数组的分区点,我们计算分区点。使得两个数组中分区左侧的元素数小于分区右侧的元素数;
- 找到较短数组的分区点partition1,利用公式找到较长数组的分区点partition2;
- 然后我们检查分区点是否在数组的边界,如果没有,我们检查分区点处元素是否形成有效的中位数; 如果没有,我们可以相应的调整分区点;
- 如果分区点位于数组的边界或者分区点处的元素形成有效的中位数,我们可以计算两个数组的中位数;
- 然后,我们计算两个数组中分区左侧的最大元素和两个数组中分区右侧的最小元素,如果较短数组中分区左侧的最大元素小于或等于较长数组中分区右侧的最小元素 ,并且 较短数组中分区右侧的最小元素大于等于较长数组中分区左侧的最大元素 ,然后表明我们找到了中位数;
- 如果合并后数组的长度是偶数,我们取分区左侧最大元素和分区右侧最小元素的平均值;如果合并后数组的长度是奇数,我们取分区左侧最大元素作为作为中位数
代码如下:
class Solution {
public:
double findMedianSortedArrays(vector& nums1, vector& nums2) {
//记录两个数组的长度大小
int m = nums1.size();
int n = nums2.size();
//确保第一个数组始终是较短数组
if (m > n)
{
return findMedianSortedArrays(nums2, nums1);
}
//在较短数组的区间 【0,m】之间里查找出合适的分区点
//使得较短数组满足我们需要的条件
int left = 0;
int right = m;
while (left <= right) {
//找到较短数组的分区点partition1
int partition1 = (left + right) / 2;
//利用公式找到较长数组的分区点partition2
int partition2 = (m + n + 1) / 2 - partition1;
//然后我们检查分区点是否在数组的边界,如果没有,我们检查分区点处元素是否形成有效的中位数
//如果没有,我们可以相应的调整分区点
//较短数组找到分区点后,因为数组是已经排好序的
//当 partition1=0 时,说明较小数组分割线左边没有值,为了不影响
//nums1[partition1] <= nums2[partition2]和 Math.max(maxLeft1, maxLeft2)的判断
//所以将它设置为int的最小值,即INT_MIN
int maxLeft1 = (partition1 == 0) ? INT_MIN : nums1[partition1 - 1];
//较短数组找到分区点后,因为数组是已经排好序的
//partition1 等于较小数组的长度时,说明较小数组分割线右边没有值,为了不影响
// nums2[partition2] <= nums1[partition1] 和 Math.min(minRight1, minRight2)的判断,
//所以将它设置为int的最大值,即INT_MAX
int minRight1 = (partition1 == m) ? INT_MAX : nums1[partition1];
//较长数组找到分区点后,因为数组是已经排好序的
//当partition2等于0时,说明较长数组分割线左边没有值,为了不影响
// nums2[partition2] <= nums1[partition1] 和 Math.max(maxLeft1, maxLeft2)的判断,
//所以将它设置为int的最小值,即INT_MIN
int maxLeft2 = (partition2 == 0) ? INT_MIN : nums2[partition2 - 1];
//较长数组找到分区点后,因为数组是已经排好序的
//当partition2 == n,说明较长数组分割线右边没有值,为了不影响
//nums1[partition1] <= nums2[partition2] 和 Math.min(minRight1, minRight2)的判断,
//所以将它设置为int的最大值,即INT_MAX
int minRight2 = (partition2 == n) ? INT_MAX : nums2[partition2];
//然后,我们计算两个数组中分区左侧的最大元素和两个数组中分区右侧的最小元素
//如果较短数组中分区左侧的最大元素小于或等于较长数组中分区右侧的最小元素 并且
//较短数组中分区右侧的最小元素大于等于较长数组中分区左侧的最大元素 ,然后表明我们找到了中位数
if (maxLeft1 <= minRight2 && maxLeft2 <= minRight1) {
//如果合并后数组的长度是偶数,我们取分区左侧最大元素和分区右侧最小元素的平均值
if ((m + n) % 2 == 0)
{
return (max(maxLeft1, maxLeft2) + min(minRight1, minRight2)) / 2.0;
}
//如果合并后数组的长度是奇数,我们取分区左侧最大元素作为作为中位数
else
{
return max(maxLeft1, maxLeft2);
}
}
//此处用了maxleft1 < minRight2的取反,当较小数组中分区点的左边的值大于较长数组中分区点的右边的值
//表面右指针应该左移
else if (maxLeft1 > minRight2)
{
right = partition1 - 1;
}
//满足条件,左指针继续右移到 partition1 + 1位置处
else
{
left = partition1 + 1;
}
}
return 0.0;
}
}; 性能分析:
- 时间复杂度:O(logmin(m,n))),其中 m 和 n 分别是数组 nums1 和 nums2的长度。查找的区间是 [0,m],而该区间的长度在每次循环之后都会减少为原来的一半。所以,只需要执行 logm 次循环。由于每次循环中的操作次数是常数,所以时间复杂度为 O(logm)。由于我们可能需要交换 nums1 和 nums 2 使得 m≤n,因此时间复杂度是 O(logmin(m,n)))。
- 空间复杂度:因为不需要借助额外的空间,因此 空间复杂度为O(1)。
到此,本题便讲解结束了!!