一维有限差分算法推导及MATLAB代码

一维有限差分法简介

本文从一维赫姆霍兹方程出发推导出了一维有限差分算法，写出对应matlab函数代码，并使用该函数画出三层波导结构模式分布图。

1、有限差分方法

起源：1928年第一次提出用五点差分估计求解椭圆拉普拉斯方程。

优势：无需改变原方程的形式，其解为强形式解（strong form solution），有限体积和有限元为若形式解。

2 求解差分估计的一般方法

​ 一般来说，求解m阶偏导的表达式需要将泰勒展开到m阶，并使用m+1个节点。误差项为1阶。对于一个二阶线性常微分方程

$$\frac{d^2\varphi }{d{x}^2}=S_{\varphi }(1.1)$$
x为自变量$\varphi$为应变量，$S_{\varphi }$是x和$\varphi$的函数，为源项。在边界有边界条件为$\varphi (x_L)={\varphi }_L;\varphi (x_R)={\varphi }_R$。方程在开区间有效，满足区间类所有的点。对于不均匀的网格，求解拉普拉斯方程的差分项，有

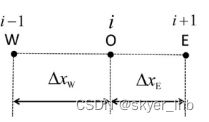
设有N个点，N-1段间隔，则第一个点和第N各点为边界条件，对于第i各点，在两侧进行泰勒展开，有：

（1.2）

(1.3)

求解一阶偏导过程如下：去掉方程（1.2）、（1.1）的高阶项，将方乘（1.2）两边同时乘上系数A，方程（1.3）两边同时乘上系数B

（1.4）

（1.5）

两式相加，为消去二阶偏导项，有

解得：

所以一阶偏导项为：

（1.6）

同理二阶偏导项为：

（1.7）

截止误差为：

（1.8）

二阶偏导的等式中不仅有结点值还有未知的高阶偏导项，忽略高阶偏导项，将原方程用差分方程表示：

，这里有N-2个等式，边界条件构成两个等式，即可求出各个点的值。

3 边界条件的应用

3.1 狄利克雷边界条件

应变量$\varphi$的值就在边界。

3.2 诺伊曼边界条件

3.3 罗宾边界条件

在这种边界条件下，在边界处指定了因变量的值及其正态梯度的线性组合。

4.一维情况赫姆霍兹方程：

（3.1）

对于结点分布如下的情况

$H_P$的二阶导数可有左右两端点值线性表示

（3.2）

差分后的一阶亥姆霍兹方程如下：

（3.3）

（3.4）

为消除其一阶导数项，令$(3.3)\cdot \frac{e{ϵ}_2}{2},(3.4)\cdot \frac{w{ϵ}_1}{2}$得到

（3.5）

（3.6）

$\frac{(3.5)+(3.6)}{\frac{e{ϵ}_2}{2}+\frac{w{ϵ}_1}{2}}$得到最终差分方程

（3.7）

其中的系数表示如下：

差分方程可以写成矩阵 $[A][H]={\beta }^2[H]$的形式，其具体表达式如下：

其中

得到矩阵方程为：

求解A矩阵本征值和本征向量即为${\beta }^2$和磁场值。

5、一维FDM算法求解模式的MATLAB函数如下

function [H,neff] = wgmodes1 (lambda, guess, nmodes, dx, eps)

% guess = n;
% eps = material_2d_space;
nx = size(eps,2);
nx = nx + 1;%nx、ny为所求磁场矩阵的大小，比介质矩阵大1

eps = [eps(1),eps,eps(nx-1)];

k = 2*pi/lambda;  % free-space wavevector

if isscalar(dx)%确定输入是不是标量，若是向量表示网格不是均匀分割的
  dx = dx*ones(1,nx+1);             % uniform grid
else
  dx = dx(:);                       % convert to column vector
  dx = [dx(1);dx;dx(length(dx))];   % pad dx on top and bottom
end

e = ones(1,nx);      e(:) = dx(2:nx+1);
w = ones(1,nx);      w(:) = dx(1:nx);
eps1 = ones(1,nx);   eps1(:) = eps(2:nx+1);
eps2 = ones(1,nx);   eps2(:) = eps(1:nx);

v = e.*eps2+w.*eps1;
ae = (2*eps2)./(e.*v);
aw = (2*eps1)./(w.*v);
ap = ((e+w).*eps1.*eps2.*k^2)./v-(2*(e.*eps1+w.*eps2)/(e.*w.*v));

ip = (1:nx);
ie = (2:nx);
iw = (1:nx-1);

A = sparse ([ip,iw,ie],[ip,ie,iw],[ap(ip),ae(iw),aw(ie)]);

shift = (guess*k)^2;
options.tol = 1e-6;
options.disp = 0;						% suppress output

[v,d] = eigs(A,speye(size(A)),nmodes,shift,options);


%S = speye(n) 返回一个主对角线元素为 1 且其他位置元素为 0 的 n×n 稀疏单位矩阵。
neff = lambda*sqrt(diag(d))/(2*pi);

H = zeros(nx,nmodes);
H=v;
% 
% 
% temp = zeros(1,nx);
% for kk = 1:nmodes
%   temp(:) = v(:,kk);
%   [mag,ii] = max(sqrt(sum(abs(temp).^2,2)));
%   if abs(temp(ii,1)) > abs(temp(ii,2))
%     jj = 1;
%   else 
%     jj = 2;
%   end
%   mag = mag*temp(ii,jj)/abs(temp(ii,jj));
%   temp = temp/mag;
%   H(:,kk) = reshape(temp(:,1),nx,ny);
% end

return;

6、建立图形文件函数如下：

function [H,neff,x] = define_geometry1D(position)

dx = 0.005;    %单位全是微米

lambda = 1.55;      % vacuum wavelength
nmodes = 1;         % number of modes to compute

n = 3.47;
%disp('defining the problem geometry');
rectangles  = [];

for i = 1: size(position,1)
    rectangles(i).min_x = position(i,1);
    rectangles(i).max_x = position(i,2);
    rectangles(i).material_type = position(i,3).^2;
end

%disp('calculating the number of cells in the problem space');


number_of_rectangles  = size(rectangles,2);

% find the minimum and maximum coordinates of a 
% box encapsulating the objects
number_of_objects = 0;

for i=1:number_of_rectangles
    number_of_objects = number_of_objects + 1;
    min_x(number_of_objects) = rectangles(i).min_x; 
    max_x(number_of_objects) = rectangles(i).max_x; 
end

if number_of_objects == 0
    fdtd_domain.min_x = 0;
    fdtd_domain.max_x = 0;
else
    fdtd_domain.min_x = min(min_x);
    fdtd_domain.max_x = max(max_x);
end

% Determining the problem space size
fdtd_domain.size_x = fdtd_domain.max_x - fdtd_domain.min_x;

% number of cells in x, y, and z directions
nx = round(fdtd_domain.size_x/dx);  

% adjust domain size by snapping to cells
fdtd_domain.size_x = nx * dx;
fdtd_domain.max_x = fdtd_domain.min_x + fdtd_domain.size_x;

material_2d_space = ones(1,nx);
x = (fdtd_domain.min_x:dx:fdtd_domain.max_x);

%disp('creating rectangles');
for ind = 1:number_of_rectangles
    % convert rectangle end coordinates to node indices 
    blx = round((rectangles(ind).min_x - fdtd_domain.min_x)/dx) + 1; 
    bux = round((rectangles(ind).max_x - fdtd_domain.min_x)/dx)+1; 
    % assign material type of the rectangle to the cells
    material_2d_space (blx:bux-1) ...
        = rectangles(ind).material_type;
end

% plot(x(1:nx),material_2d_space);

[H,neff] = wgmodes1(lambda,n,nmodes,dx,material_2d_space);

fprintf(1,'neff = %.6f\n',neff);
figure();
plot(x,abs(H));

结果如下：