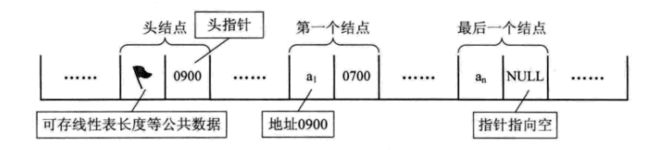
线性表的链式存储结构
单链表(线性表的链式存储)
顺序存储结构不足的解决办法
前面我们讲的线性表的顺序存储结构。它是有缺点的,最大的缺点就是插入和删除时需要移动大量元素,这显然就需要耗费时间。能不能想办法解决呢?
要解决这个问题,我们就得考虑一下导致这个问题的原因。
为什么当插入和删除时,就要移动大量元素,仔细分析后,发现原因就在于相邻两元素的存储位置也具有邻居关系。它们编号是1,2,3,…, n,它们在内存中的位置也是挨着的,中间没有空隙,当然就无法快速介入,而删除后,当中就会留出空隙,自然需要弥补。问题就出在这里。
使用数组作为存储结构的话,我们没有办法给相邻元素间预留空间(即使预留了,也无法确定大小,总有不够使的那会),因为数组找下一个元素就是通过下标+1,留了空间我们怎么确定该空间内是有效数据(使用额外的变量记录,可又如何知道有多少个空闲空间,这块也得动态调整大小),而且碎片化更加严重。
我们反正也是要让相邻元素间留有足够余地,那干脆所有的元素都不要考虑相邻位置了,哪有空位就到哪里,而只是让每个元素知道它下一个元素的位置在哪里,这样,我们可以在第一个元素时,就知道第二个元素的位置(内存地址),而找到它;在第二个元素时,再找到第三个元素的位置(内存地址)。这样所有的元素我们就都可以通过遍历而找到。
线性表链式存储结构定义
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。这就意味着,这些数据元素可以存在内存未被占用的任意位置。
以前在顺序结构中,每个数据元素只需要存数据元素信息就可以了。现在链式结构中,除了要存数据元素信息外,还要存储它的后继元素的存储地址。
因此,为了表示每个数据元素a与其直接后继数据元素ai+1之间的逻辑关系,对数据元素ai来说,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称做指针或链。这两部分信息组成数据元素ai的存储映像,称为结点(Node)。
n个结点(a的存储映像)链结成一个链表,即为线性表(a1,a2,…,an)的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。单链表正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起。
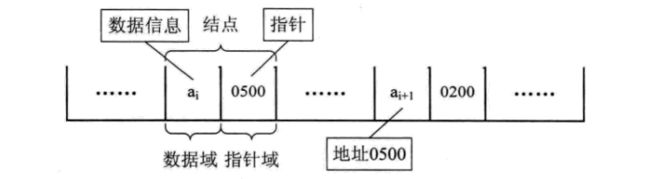
对于线性表来说,总得有个头有个尾,链表也不例外。我们把链表中第一个结点的存储位置叫做头指针,那么整个链表的存取就必须是从头指针开始进行了。之后的每一个结点,其实就是上一个的后继指针指向的位置。最后一个,当然就意味着直接后继不存在了,所以我们规定,线性链表的最后一个结点指针为“空”(通常用NULL或“^”符号表示)。
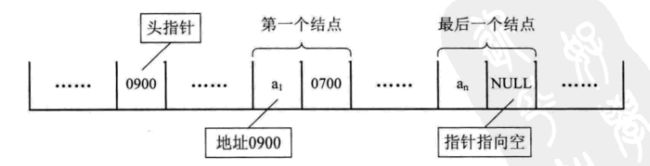
有时,我们为了更加方便地对链表进行操作,会在单链表的第一个结点前附设一个结点,称为头结点。头结点的数据域可以不存储任何信息,也可以存储如线性表的长度等附加信息,头结点的指针域存储指向第一个结点的指针。
头指针和头节点
头指针
·头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针
·头指针具有标识作用,所以常用头指针冠以链表的名字
·头指针是链表的必要元素
头节点
·头结点是为了操作的统一和方便而设立的,放在第一元素的结点之前,其数据域一般无意义(也可存放链表的长度)
·有了头结点,对在第一元素结点前插入结点和删除第一结点,其操作与其它结点的操作就统一了
·头结点不一定是链表必须要素
线性表链式存储结构描述
不带头节点的
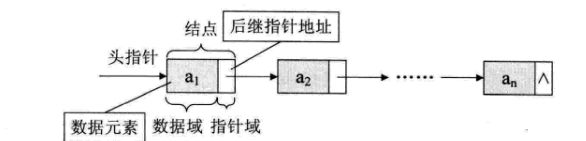
带头节点的

带头节点的空表
我在此使用的带头节点的单链表
typedef int ELemType; //用int来模拟数据项类型
typedef struct Node//数据节点/头节点公用
{
ELemType data;
struct Node* next;
}Node;
typedef Node* Linklist;//头指针
从这个结构定义中,我们也就知道,结点由存放数据元素的数据域存放后继结点地址的指针域组成。假设p是指向线性表第i个元素的指针,则该结点ai的数据域我们可以用p->data来表示,p->data的值是一个数据元素,结点ai的指针域可以用p->next来表示,p->next的值是一个指针。p->next指向谁呢?当然是指向第i+1个元素,即指向a1的指针。
单链表的初始化
主要是生成一个头节点,我们可以在主函数中定义,也可以malloc申请得到(用完记得释放)
Linklist Init_Linklist()
{
Linklist temp = (Linklist)malloc(sizeof(Node));
if (temp == NULL)
{
printf("malloc error\n");
}
else
{
temp->data = 0;//头节点的数据项我们拿来存大小/长度
temp->next = NULL;
}
return temp;
}
单链表的读取
我这里是通过其前驱的next指针(头节点的好处之一)来间接访问某个节点的data域,当然也可以直接指向该节点直接访问其数据域
ELemType GetElem_Linklist(Linklist L, int i)//返回线性表中的第i个数据元素
{
assert(L != NULL && i >= 0 && i < L->data);
while (i != 0)
{
L = L->next;
i--;
}
return L->next->data;
}
单链表的插入与删除
单链表的插入

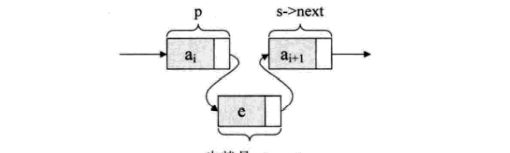
由图可知,插入需要两部,首先让e的next指向ai+1,之后再让ai的next指向e。这两部是否可以颠倒呢,不可以,因为ai+1的地址目前只有ai知道(即ai的next指针),假如我们先修改它,那么我们就弄丢了ai+1的地址,其之后的节点都丢了(内存泄露,除非我们使用额外的变量来记录它),做成了严重的错误,插入的结果也当然就错了。
插入操作,我们需要两个额外变量记录ai和e的地址,ai+i的地址在ai中存着,所以不需要记录(就算是空指针,也至少记录个NULL呢)
bool Insert_Linklist(Linklist L, int i, ELemType e)//在L线性表中的第i位插入e
{
assert(L != NULL && i >= 0 && i <= L->data);
Node* temp = (Node*)malloc(sizeof(Node));
if (temp == NULL)
{
return false;
}
else
{
L->data++;//先让个数+1,因为之后会修改L,此时不改就需要额外变量了
temp->data = e;
while (i != 0)//寻找i位置
{
L = L->next;
i--;
}
temp->next = L->next;//插入
L->next = temp;
return true;
}
}
单链表的删除
删除操作,相当于插入的反向操作,先让ai的next指向e的next指向的地方,在让e的next指针指向别处(非必要,因为该节点会被回收,存什么数据都无所谓了)。作为一个合格的C程序员,有义务自己去处理自己malloc的空间,记得free掉e节点。
bool Delect_Linklist(Linklist L, int i)//删除线性表L的第i个元素
{
assert(L != NULL && i >= 0 && i < L->data);
L->data--;
Node* pt = L->next;
while (i != 0)
{
L = L->next;
pt = pt->next;
i--;
}
L->next = pt->next;
free(pt);
return true;
}
其他函数
返回数据节点个数
对于C也不是很必要,可以直接访问L->data,C++的话,data可能是私有/保护成语,只能通过成员函数来获取
int Length_Linklist(Linklist L)//返回线性表L中的元素个数
{
return L->data;
}
判空
同上
bool IsEmpty_Linklist(Linklist L)//线性表为空则返回true,否则false
{
assert(L != NULL);
return L->data == 0;
}
清空
链表不空,我就一直删第一个元素
bool Clear_Linklist(Linklist L)//清空L;
{
while (!IsEmpty_Linklist(L))
{
Delect_Linklist(L, 0);
}
return true;
}
查找某元素下标
配合读取使用,感觉用处不大,毕竟是链表,知道下标又怎样,取数据的话,又得遍历。
int LocateElem_Linklist(Linklist L, ELemType e)//在L线性表中查找与e相等的元素下标,没有则返回-1
{
assert(L != NULL);
int i = 0;
while (L->next != NULL && e != L->next->data)
{
L = L->next;
i++;
}
return L->next == NULL ? -1 : i;
}
线性表链式存储结构的优缺点
优点
插入和删除操作不需要移动元素 ,原地修改指针O(1)
不需要一开始就确定存储空间的容量,要用多少就申请多少,不用就释放
缺点
有得就有失
需要为表示表中元素之间的逻辑关系而增加额外的存储空间(next指针)。
存取表中任位置的元素必须便利。O(n)
静态链表
由于不是每种语言都有类似指针的东西,所以就有了静态链表。实现其的方法有很多比如使用两个数组,二维数组,结构体数组,来模拟,但其都用到了数组,(可以把单个数组看作一个没有封装任何方法的顺序线性表),都避不开顺序线性表的问题,这里也就不提了。