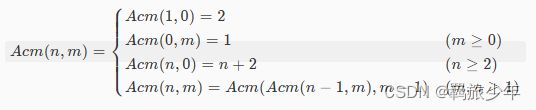算法设计与分析之递归进阶练习五题
一个不知名大学生,江湖人称菜狗
original author: jacky Li
Email : [email protected]Time of completion:2023.3.15
Last edited: 2023.3.15导读:
帮助算法设计初学者快速掌握算法设计,学习递归的思想,使得Quiet明白反反复复、永无直接才是真理!
目录
递归进阶练习
第1关:阿克曼函数
参考代码
第2关:斐波那契数列
参考代码
第3关:青蛙跳台阶问题
参考代码
第4关:猴子吃桃问题
参考代码
第5关:苹果分筐问题
参考代码
作者有言
递归进阶练习
第1关:阿克曼函数
任务描述
本关需要你根据公式来编写一个递归函数的程序,且输出答案。
相关知识
Ackerman函数是双递归函数,它的递归方程是:
编程要求
编写递归函数Acm(n,m)实现如下图所示的Acm函数,其中m、n为正整数。例如:Acm(2,1)=4,Acm(3,3)=16。
输入n和m两个整数,输出Acm(n,m)。如果n小于0或m小于0,则返回-1。
输入:
2 1输出:
4
参考代码
#include
using namespace std;
int Acm(int n,int m)
{
if(n == 1 && m == 0) return 2;
if(n == 0 && m >= 0) return 1;
if(n >= 2 && m == 0) return n + 2;
if(n >= 1 && m >= 1) return Acm(Acm(n - 1, m), m - 1);
if(n < 0 || m < 0) return -1;
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
int ans = Acm(n, m);
printf("%d", ans);
return 0;
}
第2关:斐波那契数列
任务描述
本关需要你用递归函数实现斐波那契数列。
相关知识
斐波那契数列公式为:
F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2)
编程要求
请用递归函数实现斐波那契数列,在主函数中调用该递归函数,输出第n项的值。
效果如下:
输入:
3输出:
2
参考代码
#include
using namespace std;
int F(int n)
{
if(n == 1) return 1;
if(n == 2) return 1;
if(n >= 3) return F(n - 1) + F(n - 2);
}
int main()
{
int n; cin >> n;
cout << F(n) << endl;
return 0;
}
第3关:青蛙跳台阶问题
任务描述
本关任务:一只小青蛙,每次跳台阶,他可以一下跳一个台阶,或者两个台阶,问假设有n个台阶,这只青蛙一共有多种跳的方法。
题目分析
假设小青蛙最后站在第n阶梯,那么它最后一次是怎么跳上来的呢?可以是跳一级上来,也可以是跳两级上来。假设f(n)是小青蛙跳到n个台阶的方法数。
编程要求
根据提示,在右侧编辑器补充代码,计算n个台阶共有多少总跳法。
测试说明
平台会对你编写的代码进行测试,需要输入的台阶数是大于等于1的整数,如果小于等于0,则返回-1。
测试输入:
2预期输出:
2测试输入:
5预期输出:
8
参考代码
#include
using namespace std;
int frog(int n)
{
if(n <= 0) return -1;
if(n == 1) return 1;
if(n == 2) return 2;
if(n >= 3) return frog(n - 1) + frog(n - 2);
}
int main()
{
int n; cin >> n;
cout << frog(n) << endl;
return 0;
} 第4关:猴子吃桃问题
任务描述
猴子第一天摘下若干个桃子,当天吃了一半,后面又多吃一个。第二天早上又将剩下的桃子吃掉一半,又多吃了一个。后面每天猴子都吃了前一天剩下的一半零一个。到第10天想再吃时,只剩下一个桃子。问第一天共摘了多少桃子。 如果仍然是这种吃法,第15天再吃时,也是只剩下一个桃子,那第一天摘的桃子数又是多少?
题目分析
- 可以倒着思考,第
15天为最后一天,设桃子数为S(15) - 已知
S(15)=1,第14天,设为S(14),去掉它的一半多1个就是S(15). - 只要根据
S(n-1)和S(n)的关系,就可以用递归求解得到S(1)。
编程要求
根据提示,在右侧编辑器补充代码,求解到第n天想再吃时,只剩下一个桃子,第一天共摘的桃子数。
测试说明
当输入的天数n小于1时,返回-1. 平台会对你编写的代码进行测试:
测试输入:
4预期输出:
22
参考代码
#include
using namespace std;
int PeachNumber(int n)
{
static int sum = 1;
if(n == 1) return sum;
else
{
sum = (sum + 1) * 2;
return PeachNumber(n - 1);
}
}
int main()
{
int n; cin >> n;
if(n < 1) cout << -1 << endl;
else cout << PeachNumber(n) << endl;
return 0;
} 第5关:苹果分筐问题
任务描述
本关任务:有n个苹果,现分成k筐,每筐不能为空,有多少种分法? 比如7个苹果成3筐,可以是{1,1,5}, 但这里不考虑顺序,比如我们认为{1,1,5},{1,5,1}和{5,1,1}是同一种分法。
一种思路
- 考虑第1筐,假设放入
i个苹果,它不能大于kn,因为大于该数,就会产生重复的划分。 - 剩下的
n-i个苹果,继续放到k-1个筐,它的个数不能多于k−1n−i,不能少于前一筐个数。 - 直到k==1为止。
- 比如输入 7 3
- 按该方法第1筐可放1或2
- 当第1筐放1时,第2筐可以放1或2或3
- 当第1筐放2时,第2筐只可放2或3
- ...
第1筐 第2筐 第3筐 1 1 5 1 2 4 1 3 3 2 2 3
输入格式
两个整数n,k,(6
输出格式
一个整数,即不同分法。
测试说明
平台会对你编写的代码进行测试:
测试输入:
73预期输出:
4
参考代码
#include
using namespace std;
//n个苹果分k筐,now是当前筐最少几个苹果
int divideNumber(int n,int k,int now)
{
int ans = 0;
if(k == 1) return 1;
else
{
for(int i = now; i <= (n / k); i ++)
ans = ans + divideNumber(n - i, k - 1, i);
}
return ans;
}
int main()
{
int n, k, now = 1; cin >> n >> k;
cout << divideNumber(n, k, now)<< endl;
return 0;
} 作者有言
如果感觉博主讲的对您有用,请点个关注支持一下吧,将会对此类问题持续更新……